Der Empfindlichkeitsbeiwert θ ist wie folgt definiert [1]:
| θ | 层间位移敏感系数 |
| P总 | 抗震设计情况下考虑的楼层和楼层上的总重力荷载 |
| dr | 设计层间位移，为该层顶部和底部的平均侧向位移ds的差值；在这种情况下，位移通过线性设计反应谱确定，其中 q = 1.0 |
| Vtot | 使用线性设计反应谱确定总地震楼层剪力 |
| h | 层高 |
二阶效应可以近似通过系数 1/(1 − θ) 来考虑，如果 0.1 < θ ≤ 0.2。 Für θ > 0,2 ist die geometrische Steifigkeitsmatrix bei der Berechnung der Eigenwerte und bei der Berechnung des multi-modalen Antwortspektrenverfahrens zu berücksichtigen.
Geometrische Steifigkeitsmatrix
Für dynamische Analysen sind iterative Berechnungen zur nichtlinearen Bestimmung der Theorie II. Ordnung nicht geeignet. Das Problem kann linearisiert werden und es ist hinreichend genau, die geometrische Steifigkeitsmatrix auf Basis der axialen Lasten zur Berücksichtigung der Theorie II. Ordnung heranzuziehen. Dabei wird angenommen, dass die vertikalen Lasten sich aufgrund horizontaler Einwirkungen nicht ändern und die Verformungen klein sind verglichen mit den Gebäudeabmessungen [2]. Die zu berücksichtigenden Lasten sollten denen der Bemessungssituation für Erdbeben nach EN 1990 Abschnitt 6.4.3.4 [3] entsprechen:
值:
Ed = Bemessungswert der Einwirkungen
Gk,j = Charakteristischer Wert einer ständigen Einwirkung j
Qk,i = Charakteristischer Wert einer veränderlichen Einwirkung i
Ψ2,i = Beiwert für quasi-ständige Werte der veränderlichen Einwirkungen i
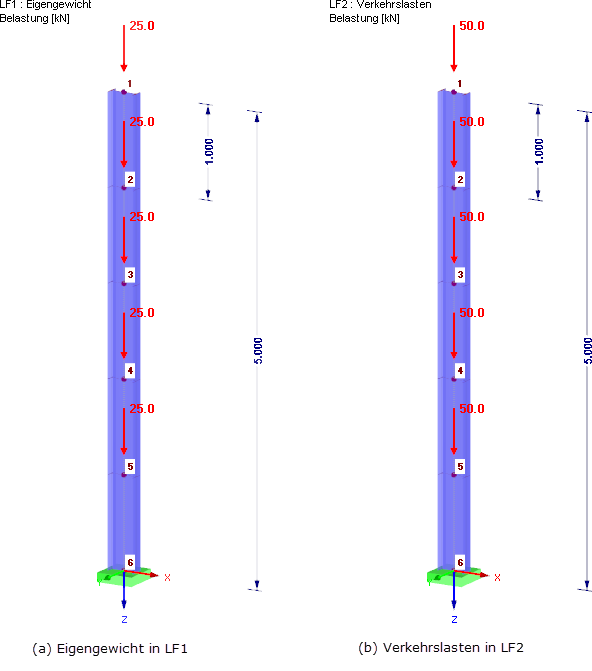
Axiale Zugkräfte erhöhen die Steifigkeit, wie beispielsweise bei einem vorgespannten Seil. Druckkräfte setzen die Steifigkeit herab und können zu einer Singularität in der Steifigkeitsmatrix führen. Die geometrische Steifigkeit Kg ist nicht abhängig von den mechanischen Eigenschaften des Systems, sondern nur von Länge L und Normalkraft N im Stab. Um das grundlegende Problem darzustellen, wird vereinfachend auf einen Kragarm zurückgegriffen, dieser ist in Bild 1 dargestellt. Die einzelnen Massepunkte des Kragarms stellen die einzelnen Geschosse eines Gebäudes dar. An diesem Gebäude soll eine dynamische Analyse unter Berücksichtigung der Theorie II. Ordnung durchgeführt werden. Die Normalkräfte Ni in den einzelnen Geschossen i = 1…n ergeben sich aus den Vertikalkräften in der Bemessungssituation Erdbeben (siehe Gleichung 2). Die Geschosshöhe ist mit hi definiert.
![将建筑物简化为悬臂结构。 各个质量点代表该楼板。 在(a)点由(a)点引起的挠度转换为等效弯矩或剪力矩[2]]](/zh/webimage/009762/467694/01-de-png.png?mw=760&hash=85d1dbfea5c6ec9f0f573d148cc6d8ae68201a9d)
Die geometrische Steifigkeitsmatrix Kg kann über die statischen Gleichgewichtsbedingungen hergeleitet werden:
Vereinfachend werden hier nur die Freiheitsgrade der horizontalen Verschiebungen dargestellt. Die gezeigte Herleitung beruht dem Ansatz des Versatzmomentes auf Basis eines linearen Verschiebungsansatzes. Dies ist für das Biegeelement eine Vereinfachung, beim Fachwerkelement eine exakte Annahme. Eine genauere Ermittlung der geometrischen Steifigkeitsmatrix für Biegebalken kann unter Verwendung eines kubischen Verschiebungsansatzes oder mit Hilfe der analytischen Lösung der Differentialgleichung der Biegelinie erfolgen. Genauere Informationen und Herleitungen werden von Werkle [4] bereitgestellt. Die geometrische Steifigkeitsmatrix Kg wird der Systemsteifigkeitsmatrix K hinzugefügt und ergibt die modifizierte Steifigkeitsmatrix Kmod:
Kmod = K + Kg (4)
Im Falle von Drucknormalkräften führt dies folglich zu einer Verringerung der Steifigkeit.
示例 Eigenfrequenzen und multi-modales Antwortspektrenverfahren unter Berücksichtigung der Theorie II. Ordnung
Nachfolgend wird gezeigt, wie die geometrische Steifigkeitsmatrix in RFEM und den Zusatzmodulen RF-DYNAM Pro berücksichtigt werden kann. Als Beispiel wird der in Bild 1 dargestellte Kragarm verwendet. Der Kragarm besteht aus fünf konzentrierten Massepunkten. Hier wirken jeweils 4.000 kg in die globale X-Richtung.
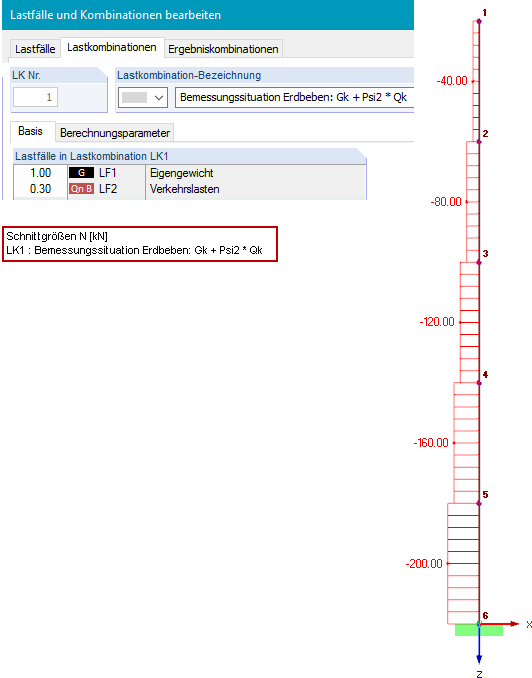
Der Querschnitt ist ein IPE 300 mit einem Material S 235 mit Iy = 8.356 ∙ 10-5 m4 und E = 2,1 ∙ 1011 N/m2. Um die geometrische Steifigkeitsmatrix bei einer dynamischen Analyse berücksichtigen zu können, wird zunächst im Hauptprogramm RFEM eine Lastkombination für die Bemessungssituation Erdbeben (siehe Gleichung 2) definiert.
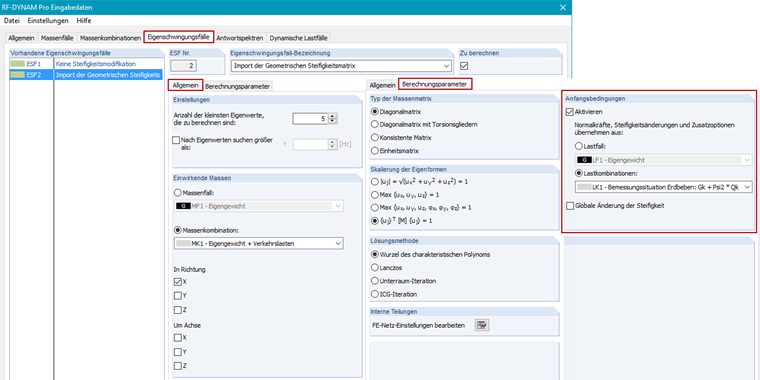
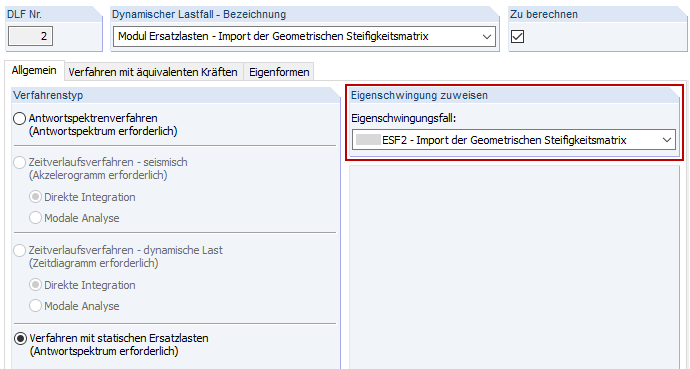
Mit RF-DYNAM Pro - Eigenschwingungen werden Eigenfrequenzen, Eigenformen und effektive Modalmassen einer Struktur ermittelt, dies kann unter Berücksichtigung verschiedenster Steifigkeitsmodifikationen geschehen (siehe Kapitel 2.4.7 im RF-DYNAM Pro Handbuch [5] und im Dlubal-Blog [6]). Zwei Eigenschwingungsfälle sind definiert. Im ESF2 wird die LK1 zur Berücksichtigung der geometrischen Steifigkeitsmatrix und damit zur Berücksichtigung der Theorie II. Ordnung importiert. Zum Vergleich ist der ESF1 definiert, dieser enthält keine Steifigkeitsmodifikationen.
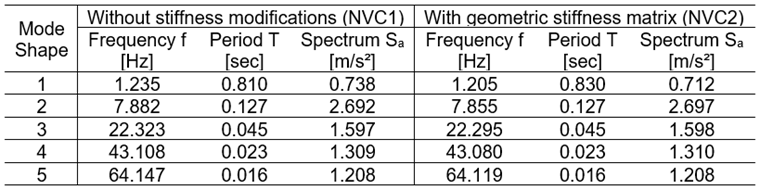
In der nachstehenden Tabelle sind die ermittelten Eigenfrequenzen f [Hz], Eigenperioden T [sec] und die aus dem Antwortspektrum abgelesenen Beschleunigungswerte Sa [m/s²], mit und ohne Berücksichtigung der geometrischen Steifigkeitsmatrix Kg resultierend aus den Normalkräften aus LK1, aufgelistet.
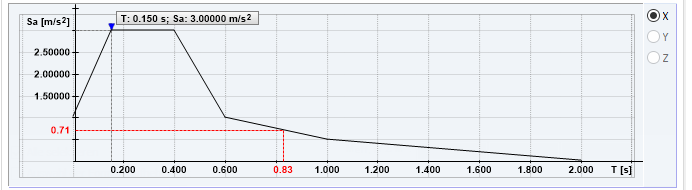
Beim multi-modalen Antwortspektrenverfahren werden mit Hilfe der Eigenfrequenzen die Beschleunigungswerte aus dem definierten Antwortspektrum abgelesen. Diese Beschleunigungswerte sind Grundlage für die Ermittlung der Ersatzlasten und Schnittgrößen des Antwortspektrenverfahrens. Die grafische Darstellung des benutzerdefinierten Antwortspektrums ist in Bild 6 gezeigt, die aus dem Antwortspektrum abgelesenen Beschleunigungswerte Sa [m/s²] für jeden Eigenwert sind in vorstehender Tabelle gelistet.
Um eine richtige Zuordnung der modifizierten Frequenzen sicherzustellen, muss der richtige Eigenschwingungsfall (ESF) im Dynamischen Lastfall (DLF) zugewiesen werden.
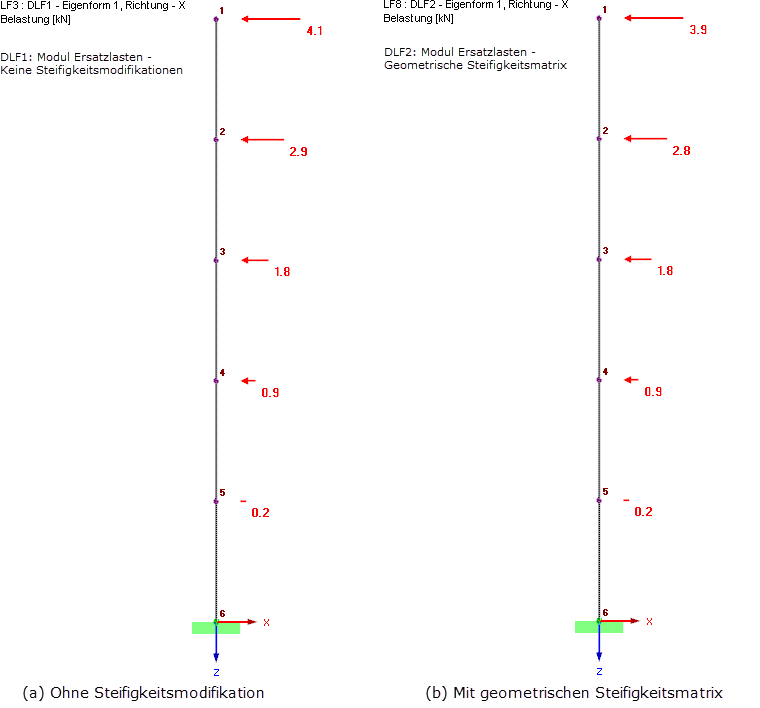
Die Berücksichtigung der geometrischen Steifigkeitsmatrix führt im Falle von Drucknormalkräften zu einer Verringerung der Eigenfrequenz und kann, wie in diesem Beispiel, zu geringeren zugehörigen Beschleunigungswerten Sa führen. Die Modifikation der Eigenfrequenzen alleine reicht nicht aus, um die Theorie II. Ordnung zu berücksichtigen, vielmehr kann dies sogar zu kleineren Ergebnissen führen und damit auf der unsicheren Seite liegen. Es ist sehr wichtig, die modifizierte Steifigkeitsmatrix auch für die Ermittlung der Schnittgrößen und Verformungen zu verwenden. In RF-DYNAM Pro - Erzwungene Schwingungen wird die modifizierte Steifigkeit automatisch zur Ermittlung der Ergebnisse des Antwortspektrenverfahrens verwendet, da hier die Berechnung innerhalb von RF-DYNAM Pro stattfindet. In RF-DYNAM Pro - Ersatzlasten werden Ersatzlasten ermittelt und in Lastfälle ins Hauptprogramm RFEM exportiert. Die Berechnung findet damit teilweise in RF-DYNAM Pro und teilweise in RFEM statt. Theoretische Hintergründe zur Berechnung der Ersatzlasten finden sich im RF-DYNAM Pro Handbuch [5]. Ein Verifikationsbeispiel [7] zeigt die Berechnung an einem konkreten Beispiel. Die ermittelten Ersatzlasten, mit und ohne Berücksichtigung der geometrischen Steifigkeitsmatrix, sind in Bild 8 dargestellt.
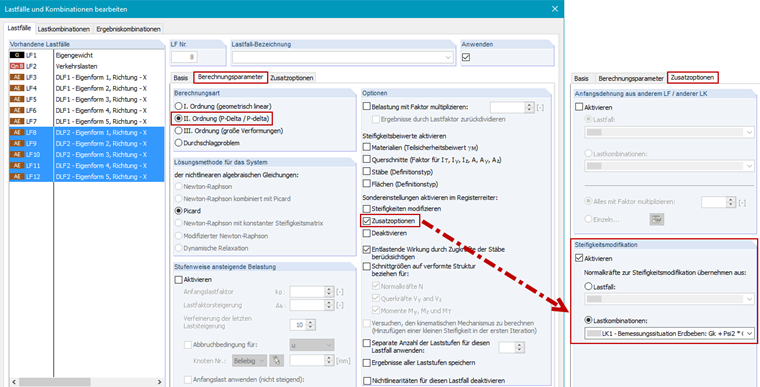
Der Export der Ersatzlasten hat viele Vorteile, aber eine korrekte Übernahme der Steifigkeitsmodifikation in die Lastfälle ist wichtig. Die Berechnungsparameter der exportierten Lastfälle müssen, wie in Bild 9 gezeigt, modifiziert werden.
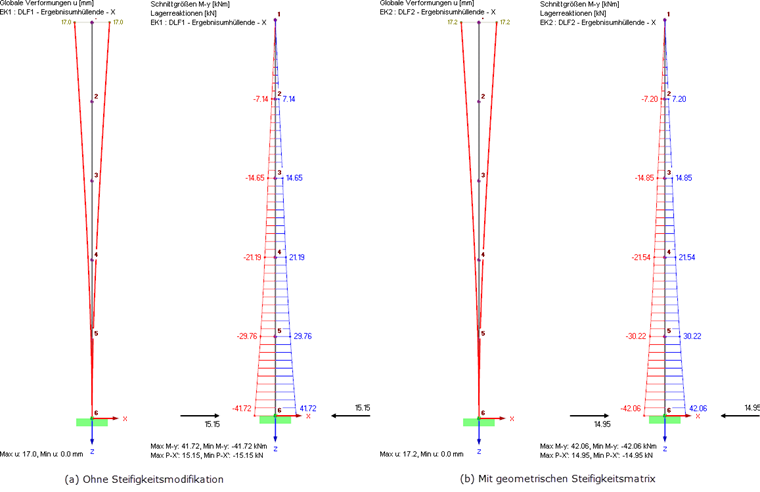
Die einzelnen Lastfälle werden mit der SRSS- oder CQC-Regel überlagert. Dies wird automatisch von RF-DYNAM Pro gesteuert und in Ergebniskombinationen exportiert. Die Ergebnisse, mit und ohne Berücksichtigung der geometrischen Steifigkeitsmatrix, sind in Bild 10 dargestellt.
Die Berücksichtigung der geometrischen Steifigkeitsmatrix führt zu größeren Verformungen und Schnittgrößen. Die angreifenden Ersatzlasten und resultierenden Auflagerlasten hingegen sind etwas kleiner unter Berücksichtigung der geometrischen Steifigkeitsmatrix.