Der Empfindlichkeitsbeiwert θ ist wie folgt definiert [1]:
| θ | Součinitel citlivosti mezipatrového posunu |
| Pcelk | Celkové tíhové zatížení na podlaží a nad ním uvažované v seizmické návrhové situaci |
| dr | návrhový posun mezi podlažími stanovený jako rozdíl průměrných bočních posunůds v horní a dolní části příslušného podlaží; v tomto případě se posuny stanoví pomocí lineárního spektra návrhové odezvy s q = 1,0 |
| Vcelk | Celkový seizmický smyk podlaží stanovený pomocí lineárního návrhového spektra odezvy |
| h | Výška poschodí |
Pokud je 0,1 < θ ≤ 0,2, lze účinky druhého řádu zohlednit přibližně součinitelem 1 / (1 − θ). Pro θ > 0,2 je třeba při výpočtu vlastních čísel a multimodální analýze spektra odezvy zohlednit geometrickou matici tuhosti.
Geometrická matice tuhosti
Pro dynamickou analýzu se iterační výpočty pro stanovení nelineárních účinků druhého řádu nehodí. Problém lze linearizovat a pro zohlednění účinků druhého řádu stačí použít geometrickou matici tuhosti z osových zatížení. Přitom se vychází z toho, že svislá zatížení se vlivem vodorovných účinků nemění a deformace jsou ve srovnání s rozměry budovy malé [2]. Die zu berücksichtigenden Lasten sollten denen der Bemessungssituation für Erdbeben nach EN 1990 Abschnitt 6.4.3.4 [3] entsprechen:
kde
Ed = návrhová hodnota zatížení
Gk,j = Charakteristischer Wert einer ständigen Einwirkung j
Qk,i = Charakteristischer Wert einer veränderlichen Einwirkung i
Ψ2,i = součinitel pro kvazistálé hodnoty proměnných účinků i
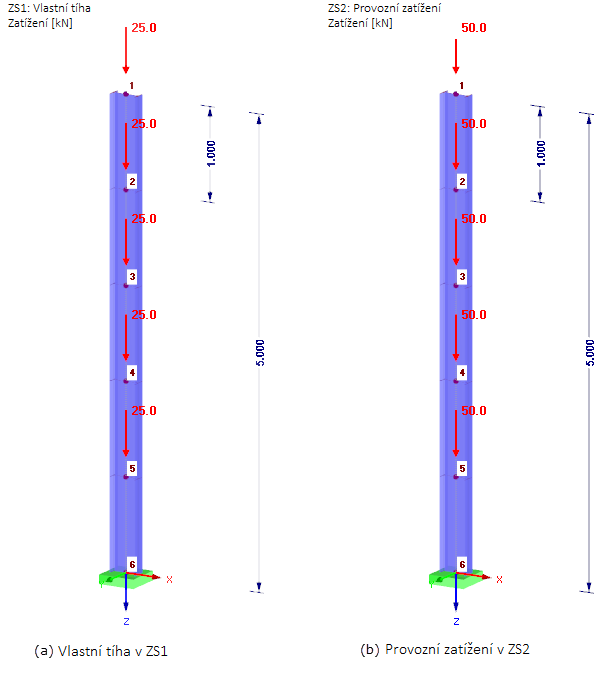
Normálové tahové síly zvyšují tuhost, jako například u předpjatého lana. Tlakové síly snižují tuhost a mohou vést k singularitám v matici tuhosti. Die geometrische Steifigkeit Kg ist nicht abhängig von den mechanischen Eigenschaften des Systems, sondern nur von Länge L und Normalkraft N im Stab. Pro ilustraci základního problému použijeme jednoduchý příklad konzoly znázorněné na obrázku 1. Jednotlivé hmotné body konzoly představují jednotlivá podlaží budovy. Budova je podrobena dynamické analýze se zohledněním účinků druhého řádu. Die Normalkräfte Ni in den einzelnen Geschossen i = 1…n ergeben sich aus den Vertikalkräften in der Bemessungssituation Erdbeben (siehe Gleichung 2). Die Geschosshöhe ist mit hi definiert.
![Redukce budovy na konzolovou konstrukci Jednotlivé hmotné body představují podlaží. Průhyb od normálových tlakových sil podle (a) se (b) přepočítá na ekvivalentní momenty posunu nebo smykové síly [2].](/cs/webimage/009762/467694/01-de-png.png?mw=760&hash=85d1dbfea5c6ec9f0f573d148cc6d8ae68201a9d)
Die geometrische Steifigkeitsmatrix Kg kann über die statischen Gleichgewichtsbedingungen hergeleitet werden:
Pro jednoduchost zde uvádíme pouze stupně volnosti vodorovných posunů. Uvedené odvození je založeno na použití klopícího momentu v důsledku účinku lineárního posunu. Jedná se o zjednodušení pro ohybový prvek a přesný předpoklad pro příhradový prvek. Přesnější stanovení geometrické matice tuhosti pro ohybové nosníky lze provést pomocí metody kubického posunu nebo pomocí analytického řešení diferenciální rovnice ohybové čáry. Podrobnější informace o teorii a odvození lze nalézt ve Werkle [4]. Die geometrische Steifigkeitsmatrix Kg wird der Systemsteifigkeitsmatrix K hinzugefügt und ergibt die modifizierte Steifigkeitsmatrix Kmod:
Kmod =K +Kg (4)
V případě tlakových osových sil tak dochází ke snížení tuhosti.
Příklad: Eigenfrequenzen und multi-modales Antwortspektrenverfahren unter Berücksichtigung der Theorie II. Ordnung
Nachfolgend wird gezeigt, wie die geometrische Steifigkeitsmatrix in RFEM und den Zusatzmodulen RF-DYNAM Pro berücksichtigt werden kann. Jako příklad použijeme konzolu znázorněnou na obrázku 1. Konzola se skládá z pěti hmotných bodů. V globálním směru X přitom vždy působí 4 000 kg.
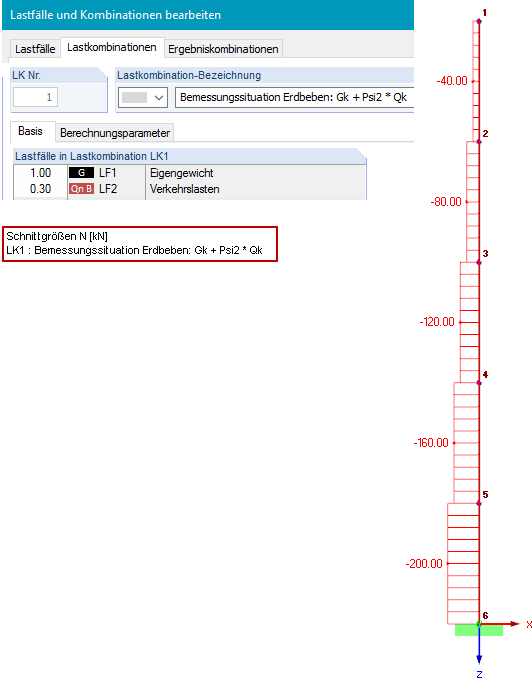
Průřez je IPE 300 z materiálu S 235 s Iy = 8 356 ∙ 10-5 m4 a E = 2,1 ∙ 1011 N/m2. Um die geometrische Steifigkeitsmatrix bei einer dynamischen Analyse berücksichtigen zu können, wird zunächst im Hauptprogramm RFEM eine Lastkombination für die Bemessungssituation Erdbeben (siehe Gleichung 2) definiert.
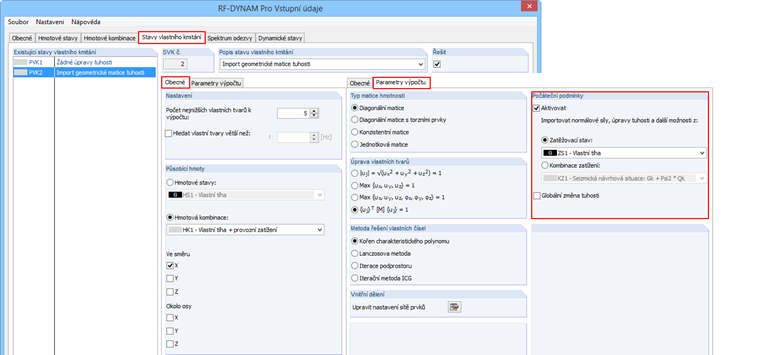
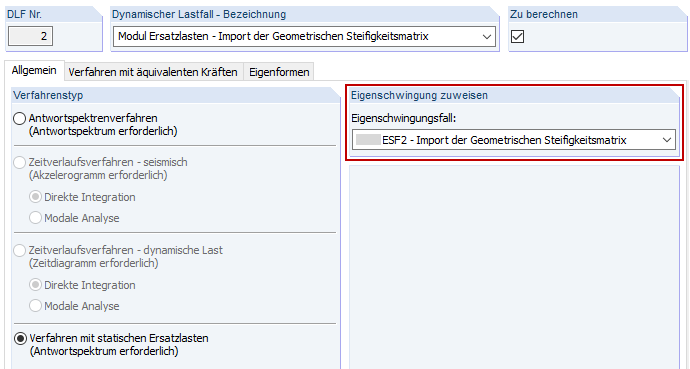
Mit RF-DYNAM Pro - Eigenschwingungen werden Eigenfrequenzen, Eigenformen und effektive Modalmassen einer Struktur ermittelt, dies kann unter Berücksichtigung verschiedenster Steifigkeitsmodifikationen geschehen (siehe Kapitel 2.4.7 im RF-DYNAM Pro Handbuch [5] und im Dlubal-Blog [6]). Zwei Eigenschwingungsfälle sind definiert. Im ESF2 wird die LK1 zur Berücksichtigung der geometrischen Steifigkeitsmatrix und damit zur Berücksichtigung der Theorie II. Ordnung importiert. Zum Vergleich ist der ESF1 definiert, dieser enthält keine Steifigkeitsmodifikationen.
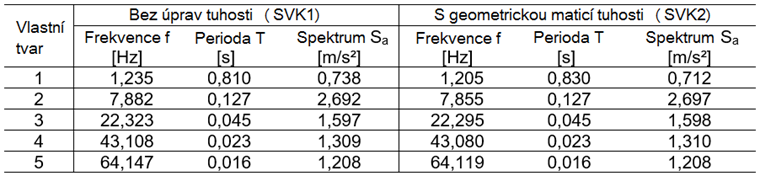
In der nachstehenden Tabelle sind die ermittelten Eigenfrequenzen f [Hz], Eigenperioden T [sec] und die aus dem Antwortspektrum abgelesenen Beschleunigungswerte Sa [m/s²], mit und ohne Berücksichtigung der geometrischen Steifigkeitsmatrix Kg resultierend aus den Normalkräften aus LK1, aufgelistet.
Při multimodální analýze spektra odezvy se s pomocí vlastních frekvencí stanoví hodnoty zrychlení z definovaného spektra odezvy. Diese Beschleunigungswerte sind Grundlage für die Ermittlung der Ersatzlasten und Schnittgrößen des Antwortspektrenverfahrens. Die grafische Darstellung des benutzerdefinierten Antwortspektrums ist in Bild 6 gezeigt, die aus dem Antwortspektrum abgelesenen Beschleunigungswerte Sa [m/s²] für jeden Eigenwert sind in vorstehender Tabelle gelistet.
Um eine richtige Zuordnung der modifizierten Frequenzen sicherzustellen, muss der richtige Eigenschwingungsfall (ESF) im Dynamischen Lastfall (DLF) zugewiesen werden.
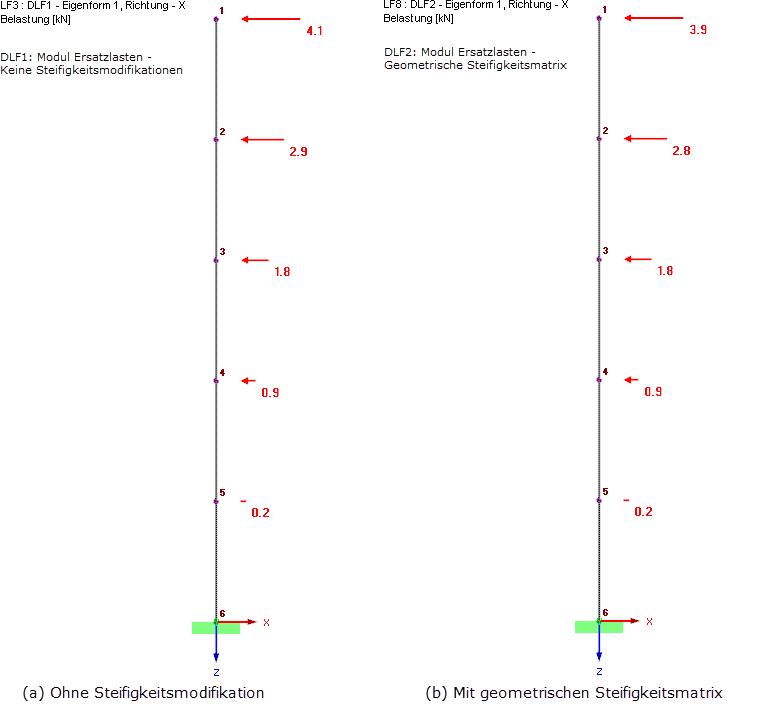
V případě tlakových normálových sil vede zohlednění geometrické matice tuhosti ke snížení vlastní frekvence a může vést k nižším hodnotám zrychlení Sa, jako v našem příkladu. Samotná úprava vlastních frekvencí není dostatečná pro zohlednění účinků druhého řádu; to může vést i k nižším výsledkům, a nebýt tak na straně bezpečnosti. Upravenou matici tuhosti je velmi důležité použít také pro stanovení vnitřních sil a deformací. In RF-DYNAM Pro - Erzwungene Schwingungen wird die modifizierte Steifigkeit automatisch zur Ermittlung der Ergebnisse des Antwortspektrenverfahrens verwendet, da hier die Berechnung innerhalb von RF-DYNAM Pro stattfindet. In RF-DYNAM Pro - Ersatzlasten werden Ersatzlasten ermittelt und in Lastfälle ins Hauptprogramm RFEM exportiert. Die Berechnung findet damit teilweise in RF-DYNAM Pro und teilweise in RFEM statt. Theoretische Hintergründe zur Berechnung der Ersatzlasten finden sich im RF-DYNAM Pro Handbuch [5]. Ein Verifikationsbeispiel [7] zeigt die Berechnung an einem konkreten Beispiel. Die ermittelten Ersatzlasten, mit und ohne Berücksichtigung der geometrischen Steifigkeitsmatrix, sind in Bild 8 dargestellt.
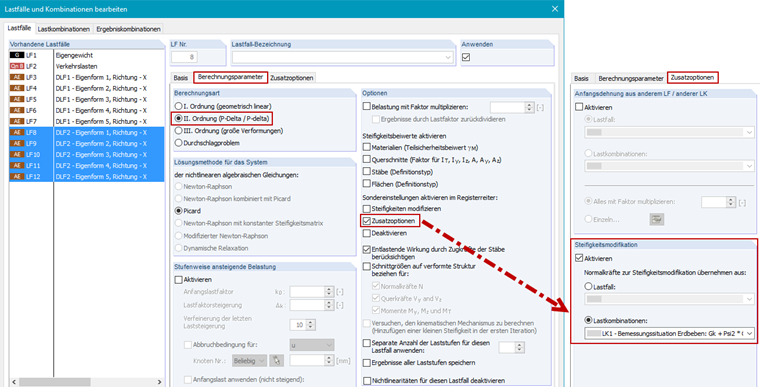
Der Export der Ersatzlasten hat viele Vorteile, aber eine korrekte Übernahme der Steifigkeitsmodifikation in die Lastfälle ist wichtig. Die Berechnungsparameter der exportierten Lastfälle müssen, wie in Bild 9 gezeigt, modifiziert werden.
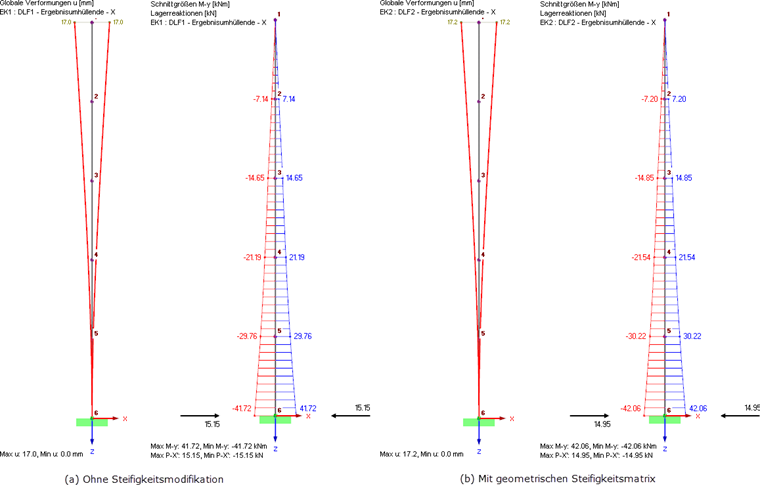
Die einzelnen Lastfälle werden mit der SRSS- oder CQC-Regel überlagert. Dies wird automatisch von RF-DYNAM Pro gesteuert und in Ergebniskombinationen exportiert. Die Ergebnisse, mit und ohne Berücksichtigung der geometrischen Steifigkeitsmatrix, sind in Bild 10 dargestellt.
Zohlednění geometrické matice tuhosti vede k větším deformacím a vnitřním silám. Die angreifenden Ersatzlasten und resultierenden Auflagerlasten hingegen sind etwas kleiner unter Berücksichtigung der geometrischen Steifigkeitsmatrix.