Le coefficient de sensibilité θ est défini comme suit [[#Refer [1]]] :
| θ | Coefficient de la sensibilité du déplacement entre les étages |
| Ptot | Charge de gravité totale sur et au-dessus de l'étage considéré dans la situation de calcul sismique |
| dr | le déplacement entre les étages de calcul déterminé comme la différence entre les déplacements latéraux moyensds entre le haut et le bas de l'étage concerné; dans ce cas, les déplacements sont déterminés à l'aide du spectre de réponse de calcul linéaire avec q = 1,0 |
| Vtot | Effort tranchant sismique total déterminé à l'aide du spectre de réponse de calcul linéaire |
| h | Hauteur d'étage |
Les effets de l'analyse du second ordre peuvent être pris en compte approximativement par un facteur égal à 1/(1 - θ), si 0,1 < θ ≤ 0,2. Pour θ > 0,2, la matrice de rigidité géométrique doit être considérée lors du calcul des valeurs propres et de l'analyse du spectre de réponse multimodal.
Matrice de rigidité géométrique
Les calculs itératifs pour la détermination non linéaire de la théorie du second ordre ne sont pas appropriés pour les analyses dynamiques. Le problème peut être linéarisé et il suffit d'utiliser la matrice de rigidité géométrique basée sur les charges axiales pour considérer la théorie du second ordre. Dabei wird angenommen, dass die vertikalen Lasten sich aufgrund horizontaler Einwirkungen nicht ändern und die Verformungen klein sind verglichen mit den Gebäudeabmessungen [2]. Die zu berücksichtigenden Lasten sollten denen der Bemessungssituation für Erdbeben nach EN 1990 Abschnitt 6.4.3.4 [3] entsprechen:
où :
Ed = valeur de calcul des effets
Gk,j = Charakteristischer Wert einer ständigen Einwirkung j
Qk,i = Charakteristischer Wert einer veränderlichen Einwirkung i
Ψ2,i = facteur pour les valeurs quasi-permanentes des actions variables i
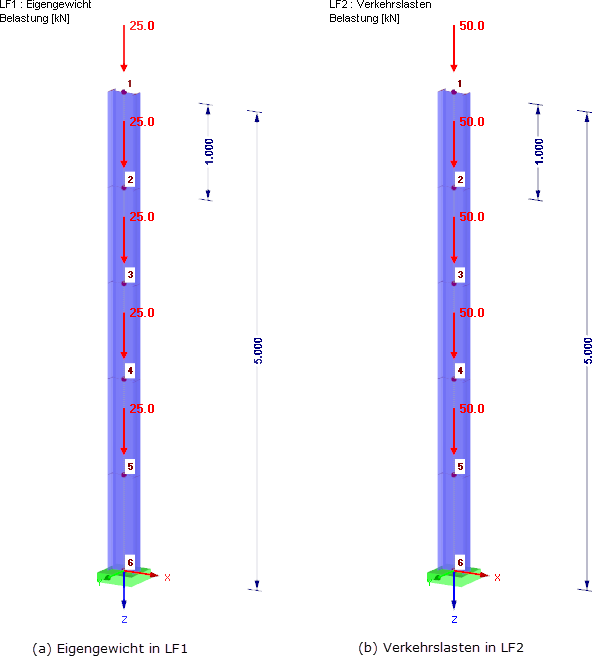
Les efforts de traction axiaux augmentent par exemple la rigidité d'un câble précontraint. Les efforts de compression réduisent la rigidité et peuvent entraîner une singularité dans la matrice de rigidité. Die geometrische Steifigkeit Kg ist nicht abhängig von den mechanischen Eigenschaften des Systems, sondern nur von Länge L und Normalkraft N im Stab. Pour illustrer ce problème, un exemple de porte-à-faux est affiché sur la Figure 01. Les points de masse individuels du porte-à-faux représentent les différents étages d'un bâtiment. Le bâtiment est soumis à une analyse dynamique selon la théorie du second ordre. Die Normalkräfte Ni in den einzelnen Geschossen i = 1…n ergeben sich aus den Vertikalkräften in der Bemessungssituation Erdbeben (siehe Gleichung 2). Die Geschosshöhe ist mit hi definiert.
![Réduction d'un bâtiment en structure en porte-à-faux. Les points de masse individuels représentent les étages. La flèche due aux efforts de compression normaux indiqués en (a) est (b) convertie en moments de déplacement ou en effort tranchant équivalents [2]]](/fr/webimage/009762/467694/01-de-png.png?mw=760&hash=85d1dbfea5c6ec9f0f573d148cc6d8ae68201a9d)
Die geometrische Steifigkeitsmatrix Kg kann über die statischen Gleichgewichtsbedingungen hergeleitet werden:
Par souci de simplification, seuls les degrés de liberté des déplacements horizontaux sont indiqués ici. La dérivation indiquée s'appuie sur l'approche du moment de basculement basée sur une approche linéaire des déplacements. Il s'agit d'une simplification de l'élément en flexion, mais d'une hypothèse exacte pour l'élément en treillis. La matrice de rigidité géométrique pour les poutres en flexion peut être déterminée avec plus de précision à l'aide d'une approche cubique des déplacements ou de la solution analytique de l'équation différentielle de la ligne en flexion. L'ouvrage [4] de H. Werkle contient des informations et des calculs plus détaillés à ce sujet. Die geometrische Steifigkeitsmatrix Kg wird der Systemsteifigkeitsmatrix K hinzugefügt und ergibt die modifizierte Steifigkeitsmatrix Kmod:
Kmod = K + Kg (4)
Dans le cas d'efforts normaux de compression, la rigidité est donc réduite.
Exemple : Eigenfrequenzen und multi-modales Antwortspektrenverfahren unter Berücksichtigung der Theorie II. Ordnung
Nachfolgend wird gezeigt, wie die geometrische Steifigkeitsmatrix in RFEM und den Zusatzmodulen RF-DYNAM Pro berücksichtigt werden kann. Le porte-à-faux représenté sur la Figure 01 est utilisé comme exemple. Le porte-à-faux est composé de cinq points de masse concentrée. Ici, 4 000 kg agissent dans la direction X globale dans chaque cas.
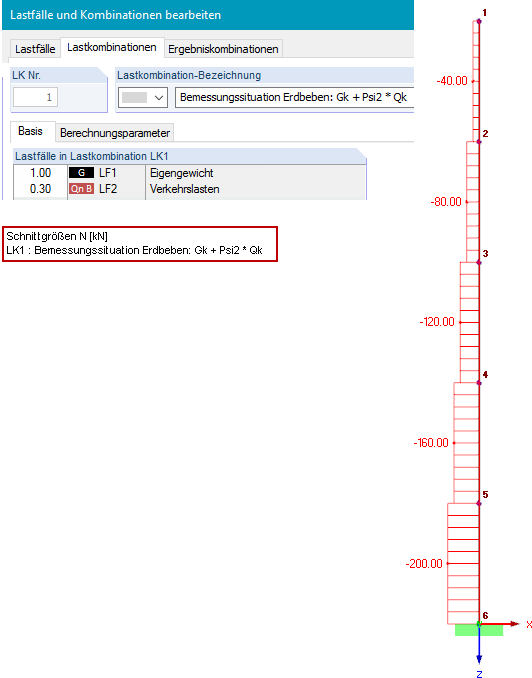
La section est un IPE 300 en matériau S 235 avec Iy = 8,356 ∙10-5 m4 et E = 2,1 ∙ 1011 N/m2. Um die geometrische Steifigkeitsmatrix bei einer dynamischen Analyse berücksichtigen zu können, wird zunächst im Hauptprogramm RFEM eine Lastkombination für die Bemessungssituation Erdbeben (siehe Gleichung 2) definiert.
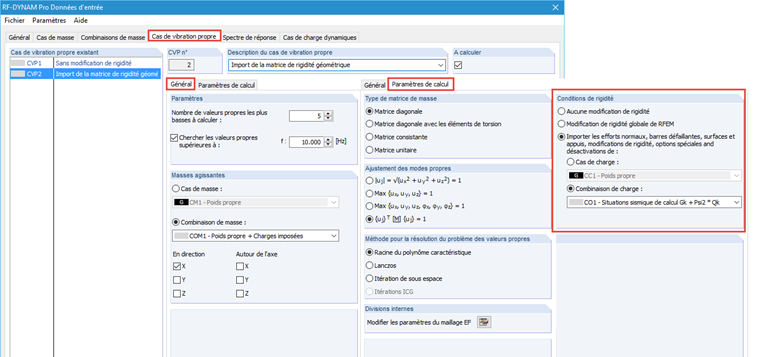
Mit RF-DYNAM Pro - Eigenschwingungen werden Eigenfrequenzen, Eigenformen und effektive Modalmassen einer Struktur ermittelt, dies kann unter Berücksichtigung verschiedenster Steifigkeitsmodifikationen geschehen (siehe Kapitel 2.4.7 im RF-DYNAM Pro Handbuch [5] und im Dlubal-Blog [6]). Zwei Eigenschwingungsfälle sind definiert. Im ESF2 wird die LK1 zur Berücksichtigung der geometrischen Steifigkeitsmatrix und damit zur Berücksichtigung der Theorie II. Ordnung importiert. Zum Vergleich ist der ESF1 definiert, dieser enthält keine Steifigkeitsmodifikationen.
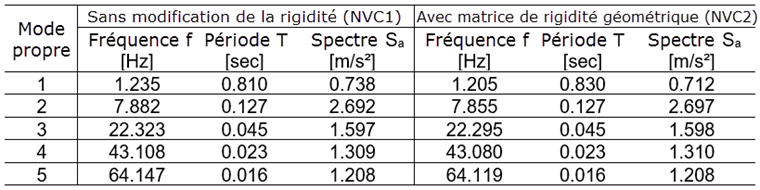
In der nachstehenden Tabelle sind die ermittelten Eigenfrequenzen f [Hz], Eigenperioden T [sec] und die aus dem Antwortspektrum abgelesenen Beschleunigungswerte Sa [m/s²], mit und ohne Berücksichtigung der geometrischen Steifigkeitsmatrix Kg resultierend aus den Normalkräften aus LK1, aufgelistet.
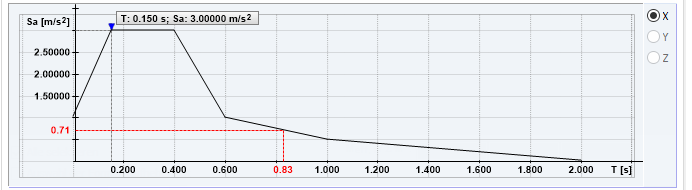
L'analyse du spectre de réponse multimodal utilise les fréquences propres pour déterminer les valeurs d'accélération à partir du spectre de réponse défini. Diese Beschleunigungswerte sind Grundlage für die Ermittlung der Ersatzlasten und Schnittgrößen des Antwortspektrenverfahrens. Die grafische Darstellung des benutzerdefinierten Antwortspektrums ist in Bild 6 gezeigt, die aus dem Antwortspektrum abgelesenen Beschleunigungswerte Sa [m/s²] für jeden Eigenwert sind in vorstehender Tabelle gelistet.
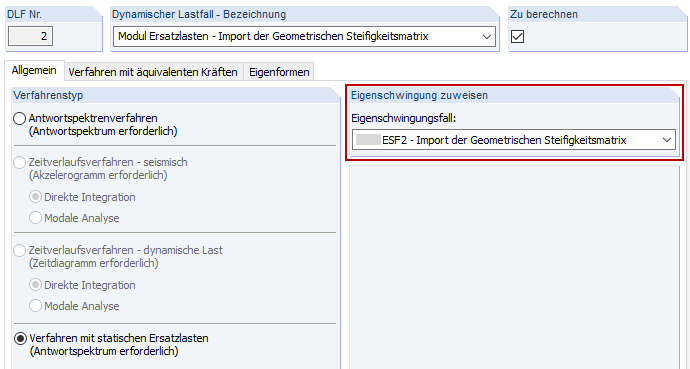
Um eine richtige Zuordnung der modifizierten Frequenzen sicherzustellen, muss der richtige Eigenschwingungsfall (ESF) im Dynamischen Lastfall (DLF) zugewiesen werden.
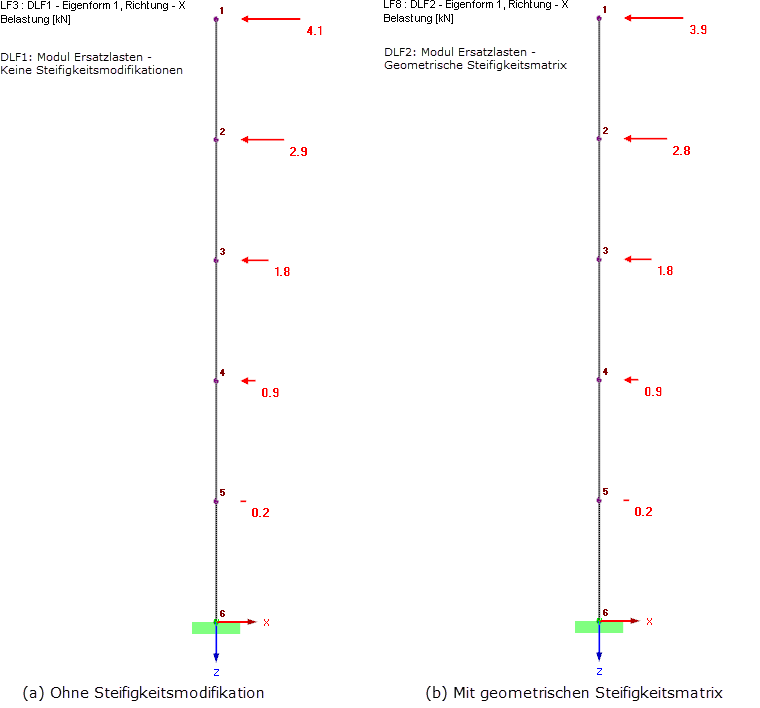
Dans le cas d'efforts normaux de compression, la considération de la matrice de rigidité géométrique entraîne une réduction de la fréquence propre et peut entraîner des valeurs d'accélération Sa plus faibles, comme dans notre exemple. La modification des fréquences propres n'est pas suffisante pour considérer la théorie du second ordre. Cette méthode permet d'obtenir des résultats plus petits et pouvant donc être erronés. Il est très important d'utiliser la matrice de rigidité modifiée pour la détermination des efforts internes et des déformations. In RF-DYNAM Pro - Erzwungene Schwingungen wird die modifizierte Steifigkeit automatisch zur Ermittlung der Ergebnisse des Antwortspektrenverfahrens verwendet, da hier die Berechnung innerhalb von RF-DYNAM Pro stattfindet. In RF-DYNAM Pro - Ersatzlasten werden Ersatzlasten ermittelt und in Lastfälle ins Hauptprogramm RFEM exportiert. Die Berechnung findet damit teilweise in RF-DYNAM Pro und teilweise in RFEM statt. Theoretische Hintergründe zur Berechnung der Ersatzlasten finden sich im RF-DYNAM Pro Handbuch [5]. Ein Verifikationsbeispiel [7] zeigt die Berechnung an einem konkreten Beispiel. Die ermittelten Ersatzlasten, mit und ohne Berücksichtigung der geometrischen Steifigkeitsmatrix, sind in Bild 8 dargestellt.
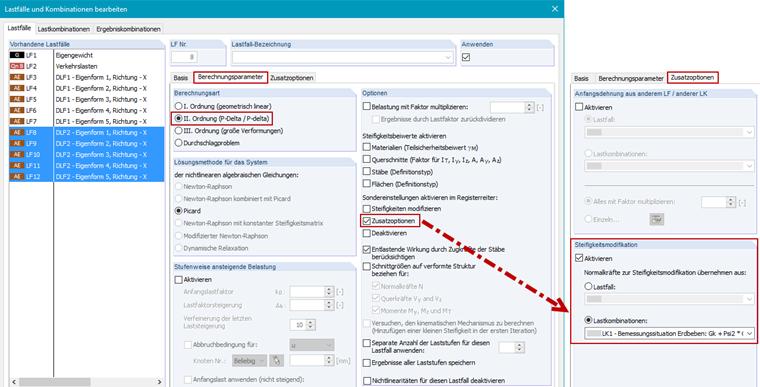
Der Export der Ersatzlasten hat viele Vorteile, aber eine korrekte Übernahme der Steifigkeitsmodifikation in die Lastfälle ist wichtig. Die Berechnungsparameter der exportierten Lastfälle müssen, wie in Bild 9 gezeigt, modifiziert werden.
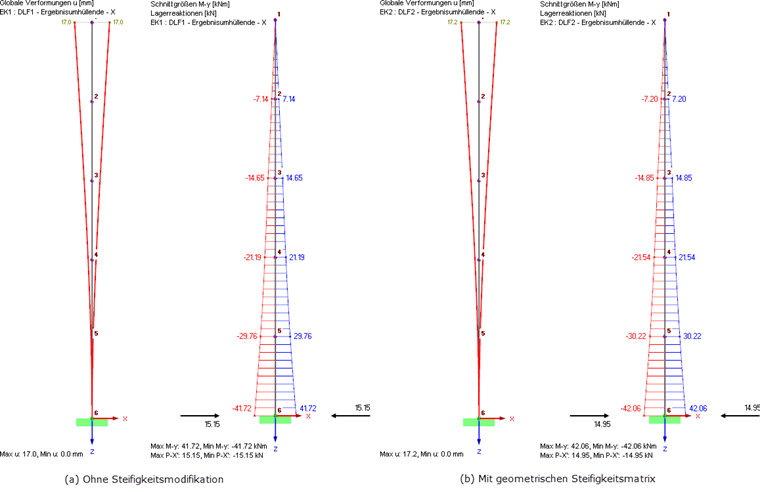
Die einzelnen Lastfälle werden mit der SRSS- oder CQC-Regel überlagert. Dies wird automatisch von RF-DYNAM Pro gesteuert und in Ergebniskombinationen exportiert. Die Ergebnisse, mit und ohne Berücksichtigung der geometrischen Steifigkeitsmatrix, sind in Bild 10 dargestellt.
La considération de la matrice de rigidité géométrique engendre des déformations et des efforts internes plus importants. Die angreifenden Ersatzlasten und resultierenden Auflagerlasten hingegen sind etwas kleiner unter Berücksichtigung der geometrischen Steifigkeitsmatrix.