Der Empfindlichkeitsbeiwert θ ist wie folgt definiert [1]:
| θ | Coeficiente de sensibilidad a la deriva entre plantas |
| Ptot | Carga gravitatoria total en y por encima del piso considerado en la situación de proyecto sísmica |
| dr | el desplazamiento entre plantas de cálculo determinado como la diferencia de los desplazamientos laterales mediosds en la parte superior e inferior de la planta en cuestión; en este caso, los desplazamientos se determinan por medio del espectro de respuesta de cálculo lineal con q = 1,0 |
| Vtot | Cortante sísmico total de la planta determinado utilizando el espectro de respuesta de cálculo lineal |
| h | Altura de la planta |
Los efectos de segundo orden se pueden considerar aproximadamente mediante un factor igual a 1/(1 − θ), si 0,1 < θ ≤ 0,2. Für θ > 0,2 ist die geometrische Steifigkeitsmatrix bei der Berechnung der Eigenwerte und bei der Berechnung des multi-modalen Antwortspektrenverfahrens zu berücksichtigen.
Matriz de rigidez geométrica
Für dynamische Analysen sind iterative Berechnungen zur nichtlinearen Bestimmung der Theorie II. Ordnung nicht geeignet. Das Problem kann linearisiert werden und es ist hinreichend genau, die geometrische Steifigkeitsmatrix auf Basis der axialen Lasten zur Berücksichtigung der Theorie II. Ordnung heranzuziehen. Dabei wird angenommen, dass die vertikalen Lasten sich aufgrund horizontaler Einwirkungen nicht ändern und die Verformungen klein sind verglichen mit den Gebäudeabmessungen [2]. Die zu berücksichtigenden Lasten sollten denen der Bemessungssituation für Erdbeben nach EN 1990 Abschnitt 6.4.3.4 [3] entsprechen:
Donde
Ed = Bemessungswert der Einwirkungen
Gk,j = Charakteristischer Wert einer ständigen Einwirkung j
Qk,i = Charakteristischer Wert einer veränderlichen Einwirkung i
Ψ2,i = Beiwert für quasi-ständige Werte der veränderlichen Einwirkungen i
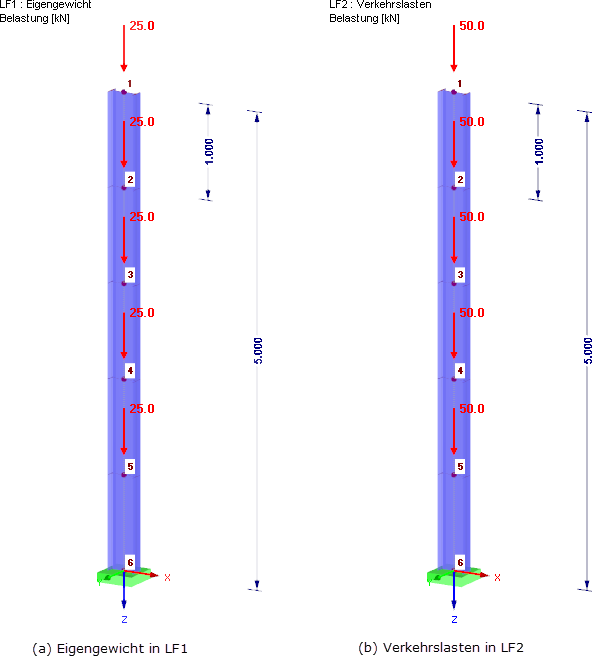
Axiale Zugkräfte erhöhen die Steifigkeit, wie beispielsweise bei einem vorgespannten Seil. Druckkräfte setzen die Steifigkeit herab und können zu einer Singularität in der Steifigkeitsmatrix führen. Die geometrische Steifigkeit Kg ist nicht abhängig von den mechanischen Eigenschaften des Systems, sondern nur von Länge L und Normalkraft N im Stab. Um das grundlegende Problem darzustellen, wird vereinfachend auf einen Kragarm zurückgegriffen, dieser ist in Bild 1 dargestellt. Die einzelnen Massepunkte des Kragarms stellen die einzelnen Geschosse eines Gebäudes dar. An diesem Gebäude soll eine dynamische Analyse unter Berücksichtigung der Theorie II. Ordnung durchgeführt werden. Die Normalkräfte Ni in den einzelnen Geschossen i = 1…n ergeben sich aus den Vertikalkräften in der Bemessungssituation Erdbeben (siehe Gleichung 2). Die Geschosshöhe ist mit hi definiert.
![Reducción de un edificio a una estructura en voladizo. Los puntos de masa individuales representan los pisos. La flecha debida a los esfuerzos normales de compresión mostrados en (a) se (b) convierte en momentos de desplazamiento equivalentes o esfuerzos cortantes [2]]](/es/webimage/009762/467694/01-de-png.png?mw=760&hash=85d1dbfea5c6ec9f0f573d148cc6d8ae68201a9d)
Die geometrische Steifigkeitsmatrix Kg kann über die statischen Gleichgewichtsbedingungen hergeleitet werden:
Para simplificar, aquí solo se muestran los grados de libertad del desplazamiento horizontal. La derivación que se muestra se basa en el enfoque del momento de vuelco debido a la aplicación del desplazamiento lineal. Esta es una simplificación para el elemento de flexión y una hipótesis precisa para el elemento de cercha. Se puede obtener una determinación más precisa de la matriz de rigidez geométrica para las barras de flexión utilizando la aproximación de desplazamiento cúbico o la solución analítica de la ecuación diferencial de la línea de flexión. Werkle [4] proporciona más información sobre teorías y derivaciones. Die geometrische Steifigkeitsmatrix Kg wird der Systemsteifigkeitsmatrix K hinzugefügt und ergibt die modifizierte Steifigkeitsmatrix Kmod:
Kmod = K + Kg (4)
En el caso de los esfuerzos normales de compresión, esto conlleva a la reducción de la rigidez.
Ejemplo: Eigenfrequenzen und multi-modales Antwortspektrenverfahren unter Berücksichtigung der Theorie II. Ordnung
Nachfolgend wird gezeigt, wie die geometrische Steifigkeitsmatrix in RFEM und den Zusatzmodulen RF-DYNAM Pro berücksichtigt werden kann. Als Beispiel wird der in Bild 1 dargestellte Kragarm verwendet. Der Kragarm besteht aus fünf konzentrierten Massepunkten. Hier wirken jeweils 4.000 kg in die globale X-Richtung.
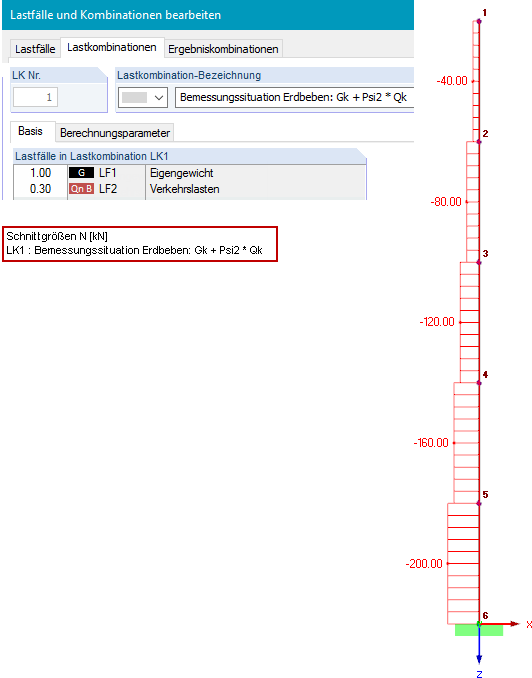
Der Querschnitt ist ein IPE 300 mit einem Material S 235 mit Iy = 8.356 ∙ 10-5 m4 und E = 2,1 ∙ 1011 N/m2. Um die geometrische Steifigkeitsmatrix bei einer dynamischen Analyse berücksichtigen zu können, wird zunächst im Hauptprogramm RFEM eine Lastkombination für die Bemessungssituation Erdbeben (siehe Gleichung 2) definiert.
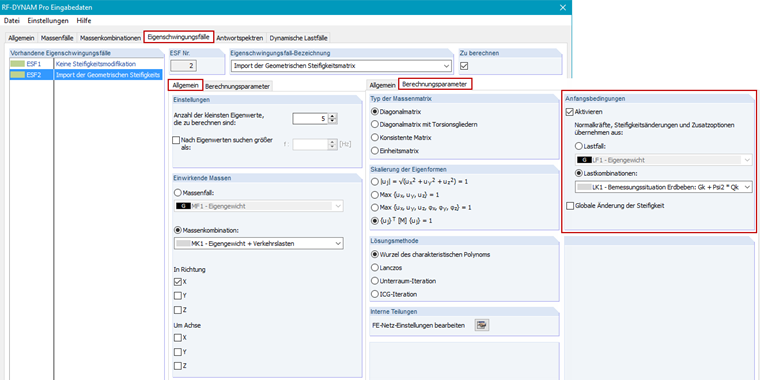
Mit RF-DYNAM Pro - Eigenschwingungen werden Eigenfrequenzen, Eigenformen und effektive Modalmassen einer Struktur ermittelt, dies kann unter Berücksichtigung verschiedenster Steifigkeitsmodifikationen geschehen (siehe Kapitel 2.4.7 im RF-DYNAM Pro Handbuch [5] und im Dlubal-Blog [6]). Zwei Eigenschwingungsfälle sind definiert. Im ESF2 wird die LK1 zur Berücksichtigung der geometrischen Steifigkeitsmatrix und damit zur Berücksichtigung der Theorie II. Ordnung importiert. Zum Vergleich ist der ESF1 definiert, dieser enthält keine Steifigkeitsmodifikationen.
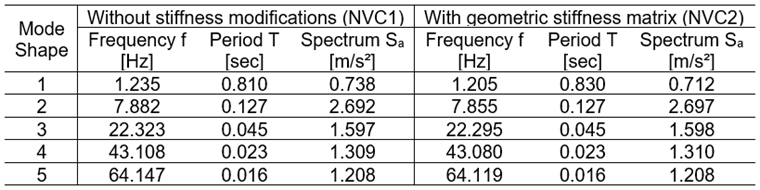
In der nachstehenden Tabelle sind die ermittelten Eigenfrequenzen f [Hz], Eigenperioden T [sec] und die aus dem Antwortspektrum abgelesenen Beschleunigungswerte Sa [m/s²], mit und ohne Berücksichtigung der geometrischen Steifigkeitsmatrix Kg resultierend aus den Normalkräften aus LK1, aufgelistet.
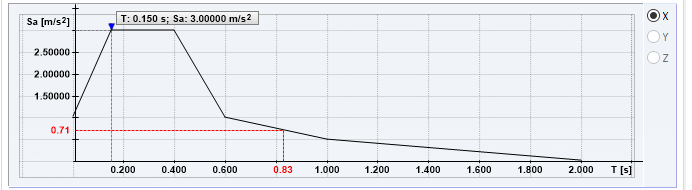
Beim multi-modalen Antwortspektrenverfahren werden mit Hilfe der Eigenfrequenzen die Beschleunigungswerte aus dem definierten Antwortspektrum abgelesen. Diese Beschleunigungswerte sind Grundlage für die Ermittlung der Ersatzlasten und Schnittgrößen des Antwortspektrenverfahrens. Die grafische Darstellung des benutzerdefinierten Antwortspektrums ist in Bild 6 gezeigt, die aus dem Antwortspektrum abgelesenen Beschleunigungswerte Sa [m/s²] für jeden Eigenwert sind in vorstehender Tabelle gelistet.
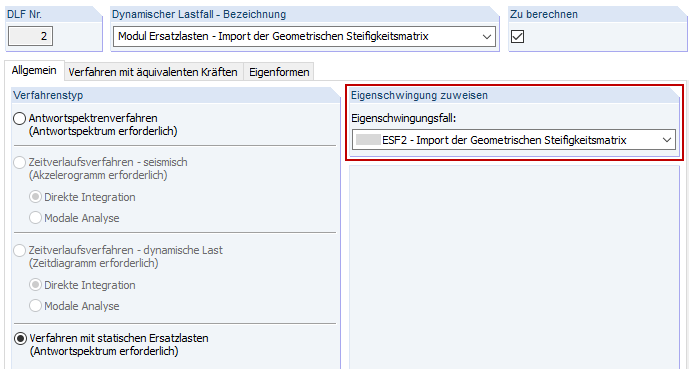
Um eine richtige Zuordnung der modifizierten Frequenzen sicherzustellen, muss der richtige Eigenschwingungsfall (ESF) im Dynamischen Lastfall (DLF) zugewiesen werden.
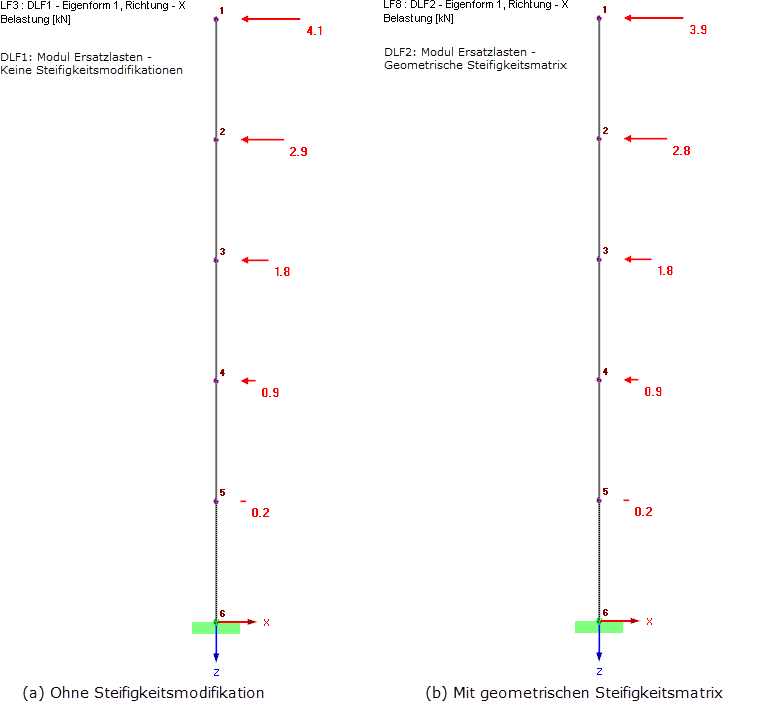
Die Berücksichtigung der geometrischen Steifigkeitsmatrix führt im Falle von Drucknormalkräften zu einer Verringerung der Eigenfrequenz und kann, wie in diesem Beispiel, zu geringeren zugehörigen Beschleunigungswerten Sa führen. Die Modifikation der Eigenfrequenzen alleine reicht nicht aus, um die Theorie II. Ordnung zu berücksichtigen, vielmehr kann dies sogar zu kleineren Ergebnissen führen und damit auf der unsicheren Seite liegen. Es ist sehr wichtig, die modifizierte Steifigkeitsmatrix auch für die Ermittlung der Schnittgrößen und Verformungen zu verwenden. In RF-DYNAM Pro - Erzwungene Schwingungen wird die modifizierte Steifigkeit automatisch zur Ermittlung der Ergebnisse des Antwortspektrenverfahrens verwendet, da hier die Berechnung innerhalb von RF-DYNAM Pro stattfindet. In RF-DYNAM Pro - Ersatzlasten werden Ersatzlasten ermittelt und in Lastfälle ins Hauptprogramm RFEM exportiert. Die Berechnung findet damit teilweise in RF-DYNAM Pro und teilweise in RFEM statt. Theoretische Hintergründe zur Berechnung der Ersatzlasten finden sich im RF-DYNAM Pro Handbuch [5]. Ein Verifikationsbeispiel [7] zeigt die Berechnung an einem konkreten Beispiel. Die ermittelten Ersatzlasten, mit und ohne Berücksichtigung der geometrischen Steifigkeitsmatrix, sind in Bild 8 dargestellt.
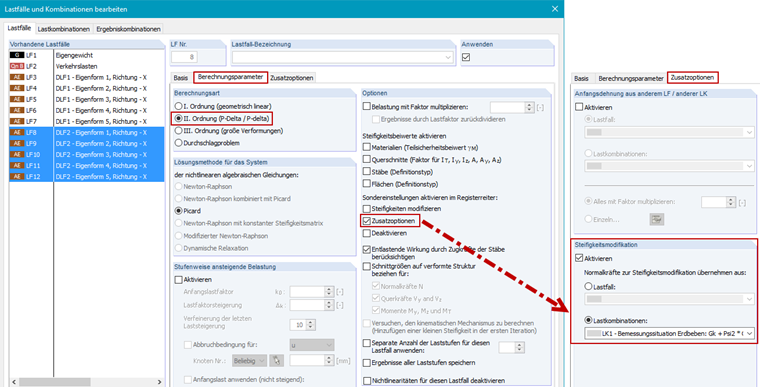
Der Export der Ersatzlasten hat viele Vorteile, aber eine korrekte Übernahme der Steifigkeitsmodifikation in die Lastfälle ist wichtig. Die Berechnungsparameter der exportierten Lastfälle müssen, wie in Bild 9 gezeigt, modifiziert werden.
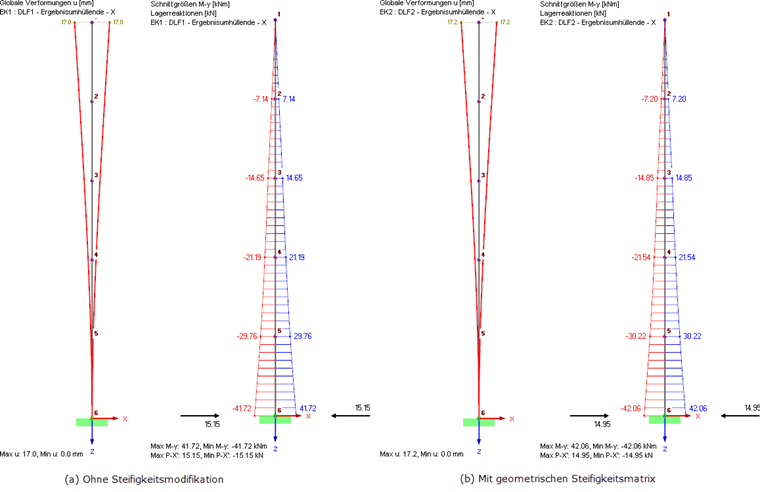
Die einzelnen Lastfälle werden mit der SRSS- oder CQC-Regel überlagert. Dies wird automatisch von RF-DYNAM Pro gesteuert und in Ergebniskombinationen exportiert. Die Ergebnisse, mit und ohne Berücksichtigung der geometrischen Steifigkeitsmatrix, sind in Bild 10 dargestellt.
Die Berücksichtigung der geometrischen Steifigkeitsmatrix führt zu größeren Verformungen und Schnittgrößen. Die angreifenden Ersatzlasten und resultierenden Auflagerlasten hingegen sind etwas kleiner unter Berücksichtigung der geometrischen Steifigkeitsmatrix.