注册成为德儒巴外部网，以获得大部分软件产品，并获得您的个人数据的专属访问权限。

创建账户

返回知识库

5835x

001539

2018-10-10

在模块 RF-/CONCRETE Columns 中计算有效长度

在 RF-CONCRETE Columns 中自动计算柱子的屈曲长度。本文接下来将介绍在模块中的必要输入以及有效长度的计算流程。

基本

在对柱子进行设计计算时，必须确定是否要考虑按照二阶理论的影响。根据相应的规范标准，构件的长细比在考虑相邻的构件的情况下与极限长细比比较。计算压杆的长细比

\begin{array}{l} \frac{1}{2} \cdot λ = \frac{l_{0}}{i} \\ mit \\ l_{0} = Knicklänge \\ i = \sqrt{\frac{I}{A}} = Trägheitsradius des ungerissenen Betonquerschnitts \end{array}

公式 1

对于普通框架，允许使用以下公式计算柱子有效长度 l₀ ：

被支撑构件

$l_{0} = 0, 5 \cdot l \cdot \sqrt{(1 \frac{k_{1}}{0, 45 k_{1}}) \cdot (1 \frac{k_{2}}{0, 45 k_{2}})}$

公式 2
无支撑构件

$l_{0} = l \cdot \max \{\begin{cases} \sqrt{1 10 \cdot \frac{k_{1} \cdot k_{2}}{k_{1} k_{2}}} \\ (1 \frac{k_{1}}{1 k_{1}}) \cdot (1 \frac{k_{2}}{1 k_{2}}) \end{cases}$

公式 3

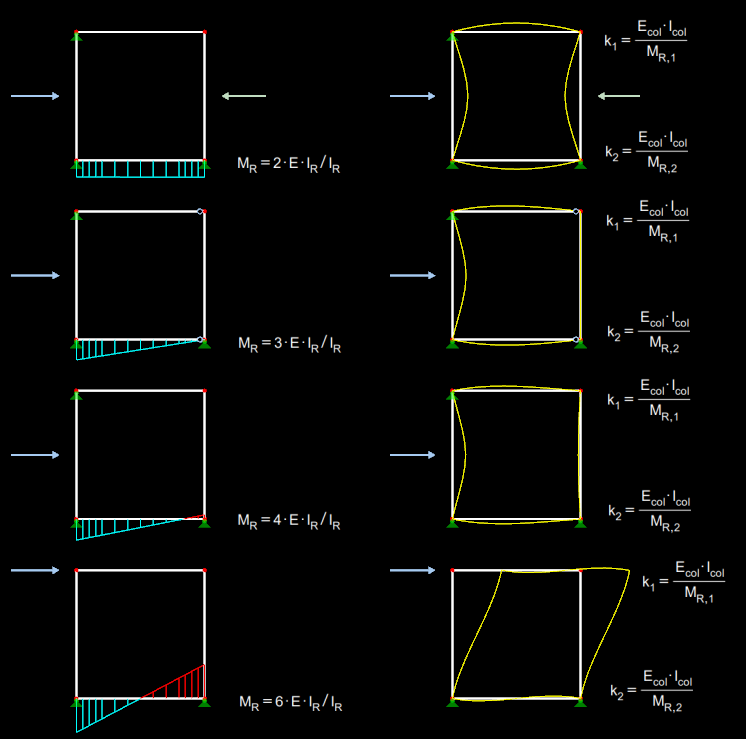
这里 k₁和 k₂是柱子两端的约束程度。见图 01 中相应的计算。

Ermittlung der Einspanngrade der Stützenenden unter Berücksichtigung der Steifigkeit der anschließenden Riegel

计算柱端旋转限制挠度考虑相关梁的刚度

梁的转动截面模量 M_R由

M_{R} = α \cdot \frac{E \cdot I_{R}}{l_{R}}

公式 4

计算。

系数 α 是由梁端铰接条件和弯矩分布产生。在图 01 中显示了这些相关性。

一般来说 k 的取值在 0.1 到 ∞ 之间。这里对于在嵌固的情况下取 0.1，对于铰接支撑取 ∞。对于嵌固的理论极限值是 0。因为在实践中刚性约束是不可能的，所以根据第2节中的规定，建议使用最小值 0.1。 5.8.3.2(3)。

有效长度也可以根据公式

l_{0} = β \cdot l_{col}

公式 5

计算。它基于[1]中的列线图，可以从中读取系数 β。系数 β 描述了柱子有效长度 l₀与柱子实际长度 l_col的比值。

示例

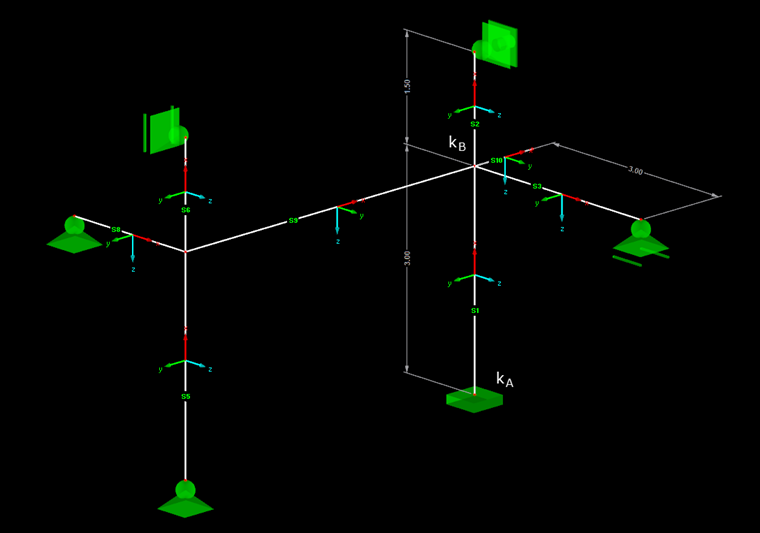
图 02 中的结构要计算有效长度。该计算比较典型，要计算柱子绕 y 轴屈曲。

结构举例

结构举例

\begin{array}{l} k_{A} = 0, 1 (eingespannter Stützenfuß) \\ k_{B} = \frac{\sum (\frac{E \cdot I_{col}}{l_{col}})}{\sum (\frac{α \cdot E \cdot I_{R}}{l_{R}})} \\ k_{B} = \frac{\frac{3.300 kN / {cm}^{2} \cdot 160.000 {cm}^{4}}{3 m} \frac{3.300 kN / {cm}^{2} \cdot 160.000 {cm}^{4}}{1, 5 m}}{\frac{3 \cdot 3.300 kN / {cm}^{2} \cdot 160.000 {cm}^{4}}{3 m}} \\ k_{B} = 1, 0 \\ l_{0} = 3 m \cdot \max \{\begin{cases} \sqrt{1 10 \cdot \frac{0, 1 \cdot 1, 0}{0, 1 1, 0}} = 1, 38 \\ (1 \frac{0, 1}{1 0, 1}) \cdot (1 \frac{1, 0}{1 1, 0}) = 1, 64 \end{cases} \\ l_{0} = 4, 91 m \end{array}

公式 6

图 03 中展示的是在模块 RF-/CONCRETE Columns 中计算得出的值。

Ergebnisse der Knicklängenberechnung in RF-BETON Stützen

Ergebnisse der Knicklängenberechnung in RF-BETON Stützen

链接

钢筋混凝土结构分析软件

参考

Ehrigsen, O.; Quast, U.: Knicklängen, Ersatzlängen und Modellstützen, Beton- und Stahlbetonbau 5, Seiten 249 - 257. Berlin: Ernst & Sohn, 2003
EN 1992-1-1 混凝土结构设计 - 第1-1部分：一般规范和建筑规范. Beuth Publishing house GmbH

下载

RFEM-Model File

屈曲稳定性有效长度混凝土柱

;