5834x

001539

2018-10-10

Determining Effective Lengths in RF-/CONCRETE Columns

Effective lengths for columns can be determined automatically with RF-/CONCRETE Columns. This article describes which entries are necessary and how the calculation of the effective lengths is performed.

Basics

When designing columns, the decision must be made for the buckling safety design whether the effects according to the second-order analysis have to be taken into account. The slenderness of the component is compared to the limiting slenderness while considering the adjacent components according to the corresponding standards. The slenderness of the compression element is calculated from

\begin{array}{l} \frac{1}{2} \cdot λ = \frac{l_{0}}{i} \\ where \\ l_{0} = effective length \\ i = \sqrt{\frac{I}{A}} = radius of gyration of uncracked concrete cross - section \end{array}

Formula 1

For normal frames, the effective lengths l₀ of the columns are allowed to be determined with the following equations:

stiffened components

$l_{0} = 0.5 \cdot l \cdot \sqrt{(1 \frac{k_{1}}{0.45 k_{1}}) \cdot (1 \frac{k_{2}}{0.45 k_{2}})}$

Formula 2
unstiffened components

$l_{0} = l \cdot \max \{\begin{cases} \sqrt{1 10 \cdot \frac{k_{1} \cdot k_{2}}{k_{1} k_{2}}} \\ (1 \frac{k_{1}}{1 k_{1}}) \cdot (1 \frac{k_{2}}{1 k_{2}}) \end{cases}$

Formula 3

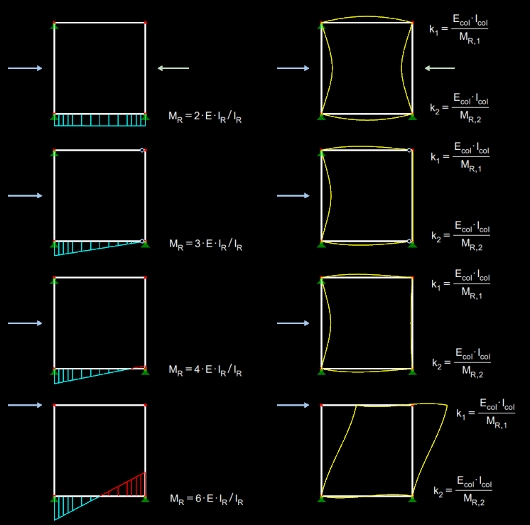
here, k₁ and k₂ are the degrees of restraint of both column ends. They are determined according to Figure 01.

Determining Degree of Restraint of Column Ends Taking into Account Stiffness of Connected Beams

The horizontal beam's rotational section modulus M_R is calculated based on

M_{R} = α \cdot \frac{E \cdot I_{R}}{l_{R}}

Formula 4

The factor α results from the release conditions of the distant beam end and the moment distribution in the beam. These correlations are also shown in Figure 01.

Basically, the degrees of restraint k should be between 0.1 and ∞. 0.1 represents the rigid restraint and ∞ the hinged support. The theoretical limit for a rigid restraint amounts to 0. Since it is impossible in practice to implement a rigid restraint, we recommend using a minimum value of 0.1 according to [2], Sec. 5.8.3.2 (3).

As an alternative, the buckling length can be determined by the equation

l_{0} = β \cdot l_{col}

Formula 5

. It is based on the nomogram from [1], where the coefficient β can be read off. The coefficient β describes the ratio of the effective length l₀ to the real column length l_col.

Example

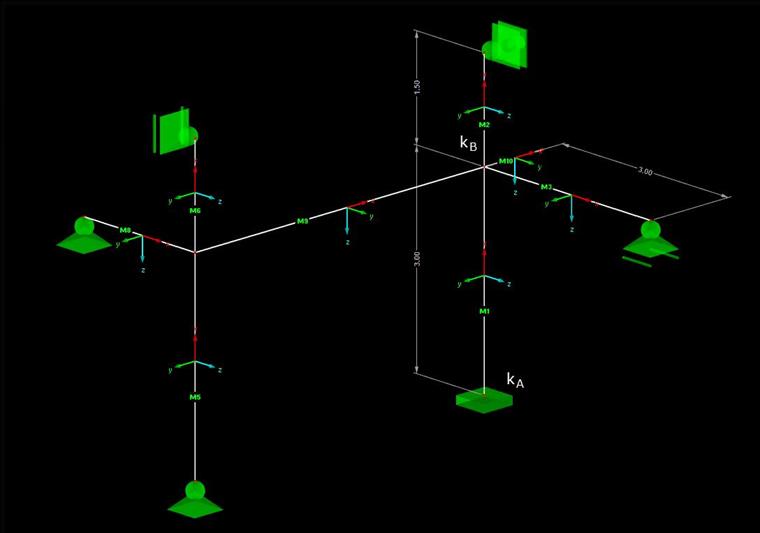
Figure 02 shows the structure to determine the effective length. The calculation is carried out in this example on member M1 for buckling around the y-axis.

System Example

\begin{array}{l} k_{A} = 0.1 (fixed column base) \\ k_{B} = \frac{\sum (\frac{E \cdot I_{col}}{l_{col}})}{\sum (\frac{α \cdot E \cdot I_{R}}{l_{R}})} \\ k_{B} = \frac{\frac{3, 300 kN / {cm}^{2} \cdot 160, 000 {cm}^{4}}{3 m} \frac{3, 300 kN / {cm}^{2} \cdot 160, 000 {cm}^{4}}{1.5 m}}{\frac{3 \cdot 3, 300 kN / {cm}^{2} \cdot 160, 000 {cm}^{4}}{3 m}} \\ k_{B} = 1.0 \\ l_{0} = 3 m \cdot \max \{\begin{cases} \sqrt{1 10 \cdot \frac{0.1 \cdot 1.0}{0.1 1.0}} = 1.38 \\ (1 \frac{0.1}{1 0.1}) \cdot (1 \frac{1.0}{1 1.0}) = 1.64 \end{cases} \\ l_{0} = 4.91 m \end{array}

Formula 6

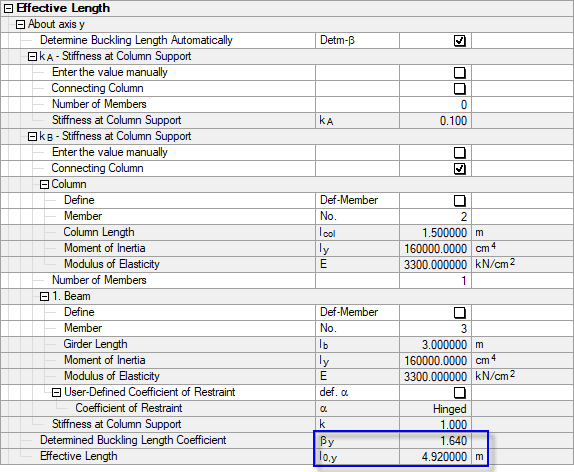
Figure 03 shows the values determined with RF-/CONCRETE Columns.

Results of Effective Length Calculation in RF-CONCRETE Columns

Links

Structural Analysis Software for Concrete Structures

References

Ehrigsen, O.; Quast, U.: Knicklängen, Ersatzlängen und Modellstützen, Beton- und Stahlbetonbau 5, Seiten 249 - 257. Berlin: Ernst & Sohn, 2003
European Committee for Standardization (CEN). (2011). Eurocode 2: Design of Concrete Structures – Part 1-1: General Rules and Rules for Buildings, EN 1992-1-1:2011-01. Berlin: Beuth Verlag GmbH.

Downloads

RFEM Model File

444 KB

;