Informacje ogólne
Podczas wymiarowania słupów należy zdecydować, czy należy uwzględnić wpływ efektów zgodnie z analizą drugiego rzędu, czy zgodnie z zasadami analizy drugiego rzędu. Przy uwzględnianiu sąsiadujących ze sobą komponentów, smukłość komponentu jest porównywana do smukłości granicznej, zgodnie z odpowiednimi normami. Smukłość elementu ściskanego jest obliczana ze wzoru
W przypadku ram normalnych długości efektywne l0 słupów można określać za pomocą następujących równań:
- komponenty usztywnione
- komponenty nieusztywnione
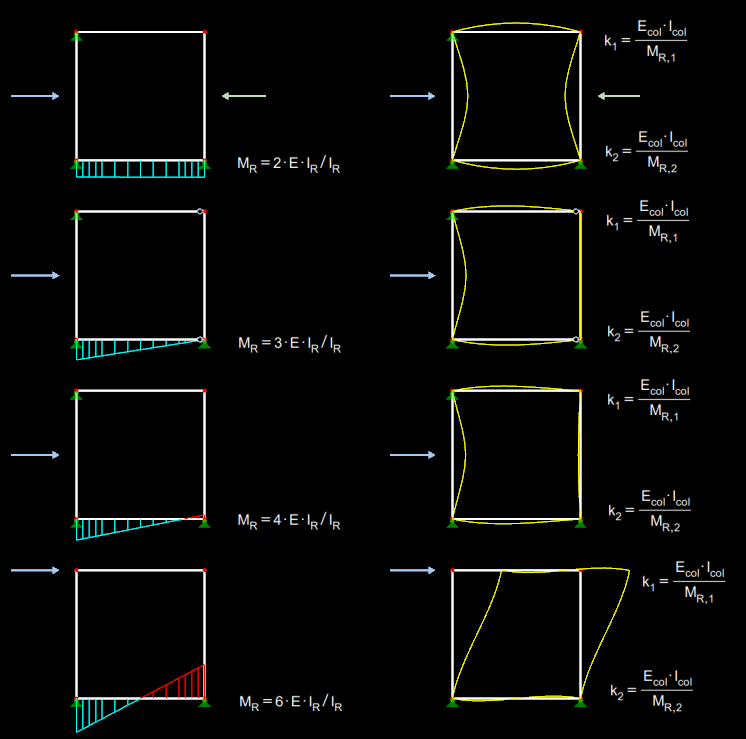
tutaj k1 i k2 są stopniami utwierdzenia obu końców słupa. Są one zdefiniowane zgodnie z Rysunkiem 01.
Obrotowy moduł przekroju belki MRobliczany jest na podstawie
.Współczynnik α wynika z warunków zwolnienia końca belki położonego dalej oraz z rozkładu momentów w belce. Te powiązania pokazano także na Rysunku 01.
Zasadniczo, stopnie utwierdzenia k powinny wynosić od 0.1 do ∞. 0.1 oznacza utwierdzenie sztywne, ∞ to podpora przegubowa. Teoretyczna granica sztywnego utwierdzenia wynosi 0. Ponieważ w praktyce nie jest możliwe wprowadzenie sztywnego utwierdzenia, zaleca się zastosowanie minimalnej wartości 0,1 zgodnie z [2] , rozdz. 5.8.3.2 (3).
Alternatywnie, długość efektywną można określić za pomocą równania
. Opiera się on na nomogramie z [1] , z którego można odczytać współczynnik β. Współczynnik β opisuje stosunek efektywnej długości l0 do rzeczywistej długości słupa lkol.Przykład
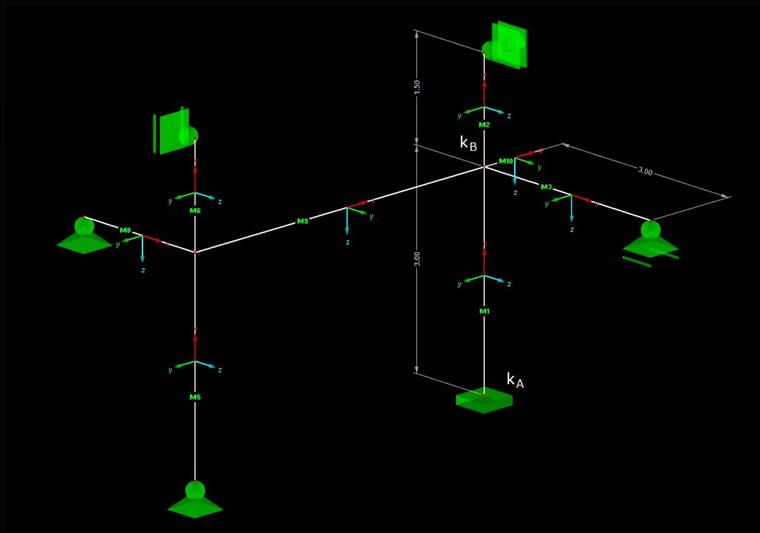
Rysunek 02 przedstawia konstrukcję, dla której należy zdefiniować długość efektywną. Obliczenia są przeprowadzane w tym przykładzie na pręcie M1 dla wyboczenia wokół osi y.
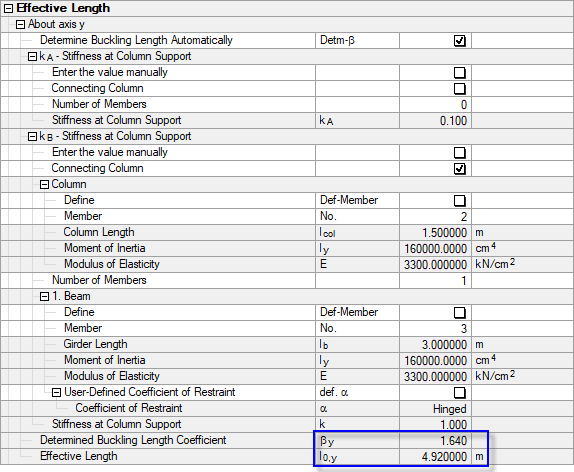
Rysunek 03 przedstawia wartości określone w module RF-/CONCRETE Columns.
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
