Grundlagen
Bei der Bemessung von Stützen muss für den Knicksicherheitsnachweis entschieden werden, ob die Auswirkungen nach Theorie II. Ordnung berücksichtigt werden müssen. Dazu wird die Schlankheit des Bauteils unter Berücksichtigung der angrenzenden Bauteile mit Grenzschlankheiten nach den entsprechenden Normen verglichen. Die Schlankheit des Druckglieds errechnet sich aus
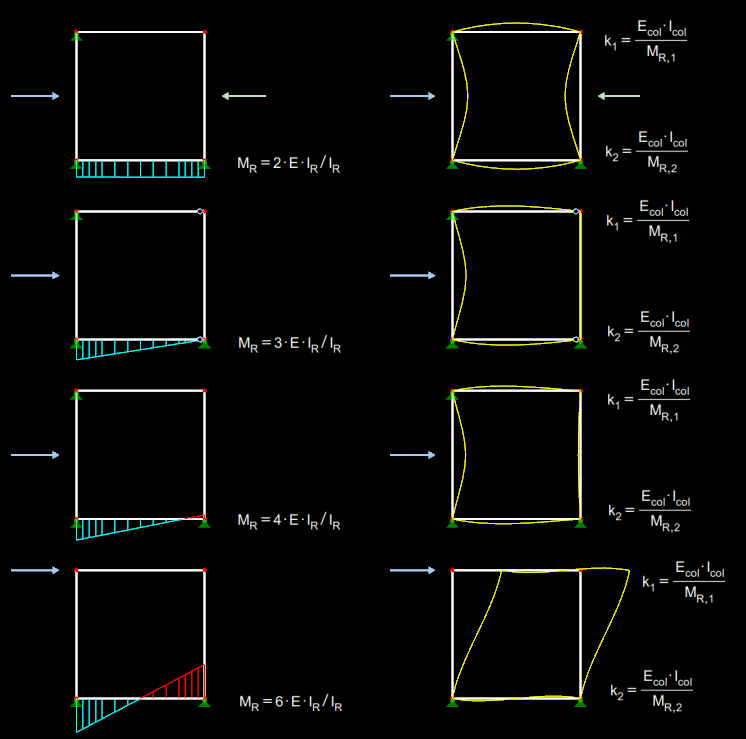
In üblichen Rahmen dürfen die Knicklängen l0 der Stützen mit den folgenden Gleichungen ermittelt werden:
- ausgesteifte Bauteile
- nicht ausgesteifte Bauteile
Hierbei sind k1 und k2 die bezogenen Einspanngrade der beiden Stützenenden. Diese werden entsprechend Bild 01 ermittelt.
Das Drehwiderstandsmoment des Riegels MR berechnet sich aus
.Der Faktor α ergibt sich aus den Gelenkbedingungen des abliegenden Riegelendes beziehungsweise dem Momentenverlauf im Riegel. Auch diese Zusammenhänge können Bild 01 entnommen werden.
Grundsätzlich sollten die Einspanngrade k zwischen 0,1 und ∞ liegen. Dabei steht 0,1 für die feste Einspannung und ∞ für die gelenkige Lagerung. Die theoretische Grenze für eine feste Einspannung ist 0. Da aber die Umsetzung einer starren Einspannung in der Praxis nicht möglich ist, wird nach [2] Abs. 5.8.3.2 (3) ein Mindestwert von 0,1 empfohlen.
Alternativ kann die Knicklänge auch mit der Gleichung
ermittelt werden. Diese beruht auf den Nomogrammen aus [1], aus welchen der Beiwert β abgelesen werden kann. Der Beiwert β bezeichnet das Verhältnis der Knicklänge l0 zur wahren Stützenlänge lcol.Beispiel
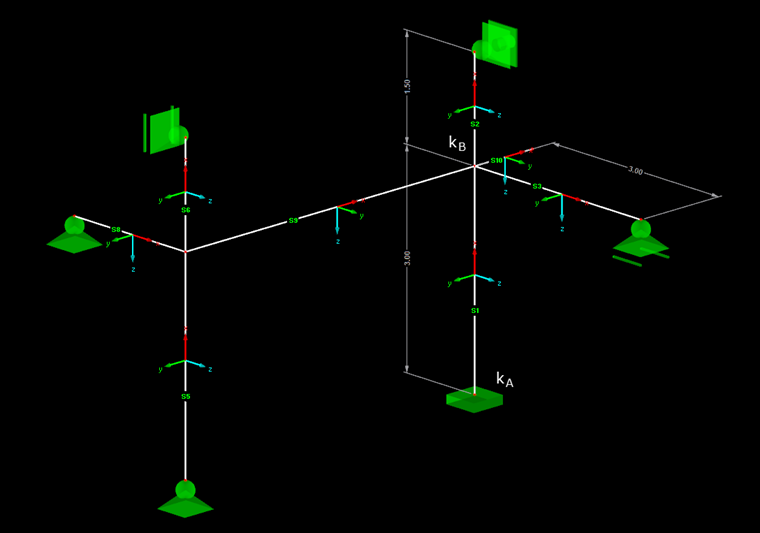
Bild 02 zeigt das System für die Ermittlung der Knicklänge. Die Berechnung soll exemplarisch an Stütze S1 für Knicken um die y-Achse durchgeführt werden.
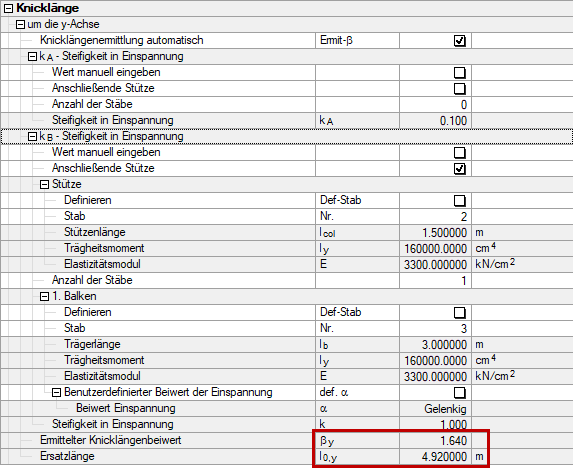
Bild 03 zeigt die von RF-/BETON Stützen ermittelten Werte.
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
