5835x

001539

10.10.2018

Výpočet vzpěrných délek v modulu RF-/CONCRETE Columns

V přídavném modulu RF-/CONCRETE Columns lze vzpěrné délky sloupů stanovit automaticky. V našem příspěvku popíšeme, které vstupní údaje je přitom třeba zadat a jak výpočet vzpěrných délek probíhá.

Základy

Při návrhu sloupů je třeba pro posouzení bezpečnosti při vzpěru rozhodnout, zda se mají zohlednit účinky druhého řádu. Přitom se štíhlost konstrukčního prvku porovnává s přihlédnutím k přilehlým dílcům s mezními hodnotami štíhlosti podle příslušných norem. Štíhlost tlačeného prvku se stanoví z výrazu

\begin{array}{l} \frac{1}{2} \cdot λ = \frac{l_{0}}{i} \\ kde \\ l_{0} = vzpěrnádélka \\ i = \sqrt{\frac{I}{A}} = poloměr setrvačnosti betonubez trhlin \end{array}

Vzorec 1

V běžných rámových konstrukcích lze vzpěrné délky l₀ sloupů vypočítat pomocí následujících rovnic:

Ztužené prvky

$l_{0} = 0, 5 \cdot l \cdot \sqrt{(1 \frac{k_{1}}{0, 45 k_{1}}) \cdot (1 \frac{k_{2}}{0, 45 k_{2}})}$

Vzorec 2
Neztužené prvky

$l_{0} = l \cdot \max \{\begin{cases} \sqrt{1 10 \cdot \frac{k_{1} \cdot k_{2}}{k_{1} k_{2}}} \\ (1 \frac{k_{1}}{1 k_{1}}) \cdot (1 \frac{k_{2}}{1 k_{2}}) \end{cases}$

Vzorec 3

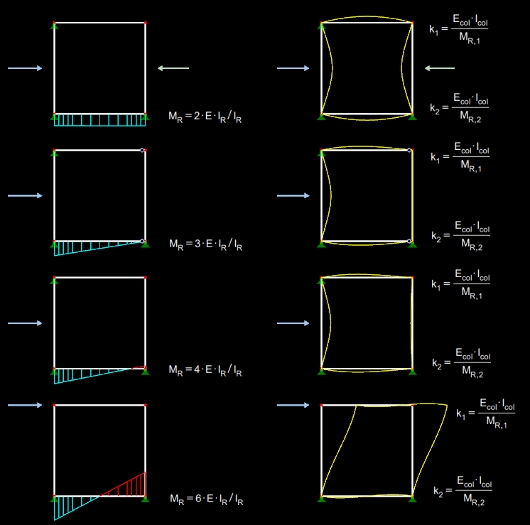
Přitom k₁ a k₂ jsou poměrné poddajnosti v natočení obou konců prutu. Stanoví se podle obr. 01.

Ermittlung der Einspanngrade der Stützenenden unter Berücksichtigung der Steifigkeit der anschließenden Riegel

Výpočet poddajnosti v natočení konců sloupu s přihlédnutím k tuhosti připojené příčle

Průřezový modul příčle v kroucení M_R se určí ze vztahu

M_{R} = α \cdot \frac{E \cdot I_{R}}{l_{R}}

Vzorec 4

Součinitel α se stanoví na základě podmínek kloubového podepření odlehlého konce příčle, respektive z průběhu momentů v příčli. Také tyto vztahy lze převzít z obr. 01.

V zásadě by měly hodnoty poměrné poddajnosti k ležet v rozmezí 0,1 a ∞. Přitom 0,1 odpovídá ohybově zcela tuhé podpoře a ∞ kloubovému podepření. Teoretická mezní hodnota pro pevné vetknutí je 0. Protože se zcela tuhé uložení v praxi vyskytuje zřídka, doporučuje se podle [2], čl. 5.8.3.2 (3) minimální hodnota 0,1.

Alternativně lze vzpěrnou délku stanovit pomocí rovnice

l_{0} = β \cdot l_{col}

Vzorec 5

. která vychází z nomogramů v [1], z nichž lze vyčíst hodnotu β. Součinitel β udává poměr vzpěrné délky l₀ a skutečné délky sloupu l_col.

Příklad

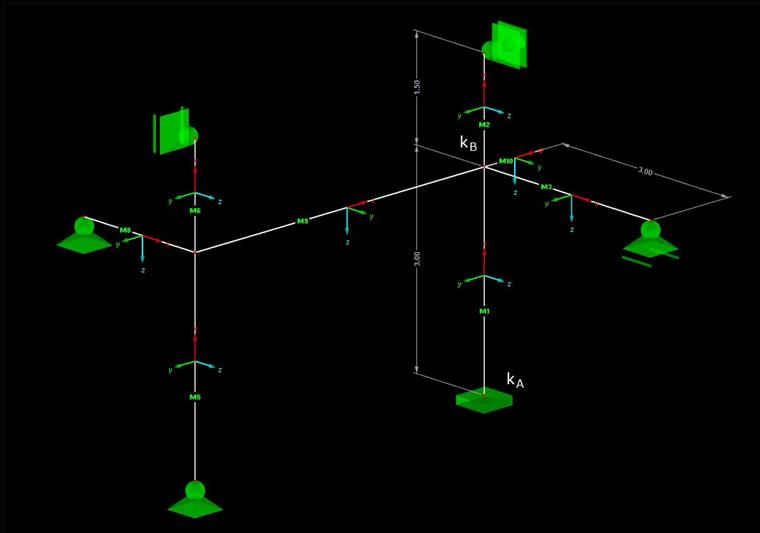
Na obr. 02 je znázorněna konstrukce pro výpočet vzpěrné délky. Výpočet se vzorově provede u sloupu S1 pro vzpěr okolo osy y.

Příklad konstrukce

\begin{array}{l} k_{A} = 0, 1 (vetknutá patkasloupu) \\ k_{B} = \frac{\sum (\frac{E \cdot I_{col}}{l_{col}})}{\sum (\frac{α \cdot E \cdot I_{R}}{l_{R}})} \\ k_{B} = \frac{\frac{3300 kN / {cm}^{2} \cdot 160000 {cm}^{4}}{3 m} \frac{3300 kN / {cm}^{2} \cdot 160000 {cm}^{4}}{1, 5 m}}{\frac{3 \cdot 3300 kN / {cm}^{2} \cdot 160000 {cm}^{4}}{3 m}} \\ k_{B} = 1, 0 \\ l_{0} = 3 m \cdot \max \{\begin{cases} \sqrt{1 10 \cdot \frac{0, 1 \cdot 1, 0}{0, 1 1, 0}} = 1, 38 \\ (1 \frac{0, 1}{1 0, 1}) \cdot (1 \frac{1, 0}{1 1, 0}) = 1, 64 \end{cases} \\ l_{0} = 4, 91 m \end{array}

Vzorec 6

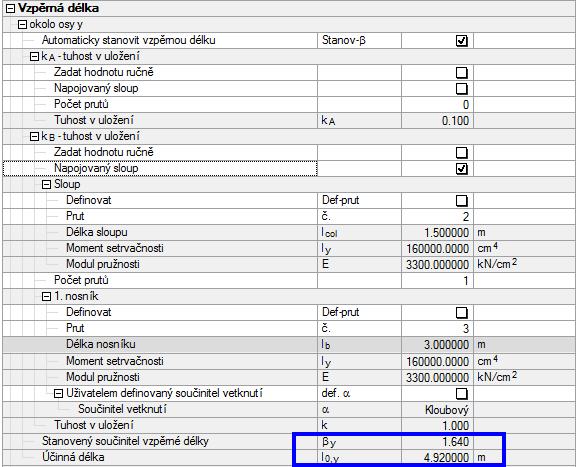
Na obr. 03 vidíme hodnoty vypočítané v modulu RF-/CONCRETE Columns.

Ergebnisse der Knicklängenberechnung in RF-BETON Stützen

Odkazy

Software pro návrh železobetonových konstrukcí

Reference

Ehrigsen, O.; Quast, U.: Knicklängen, Ersatzlängen und Modellstützen, Beton- und Stahlbetonbau 5, Seiten 249 - 257. Berlin: Ernst & Sohn, 2003
EN 1992-1-1: Navrhování betonových konstrukcí – Část 1-1: Obecná pravidla a pravidla pro pozemní stavby. Nakladatelství Beuth GmbH

Stahování

Model v programu RFEM

444 KB

;