介绍
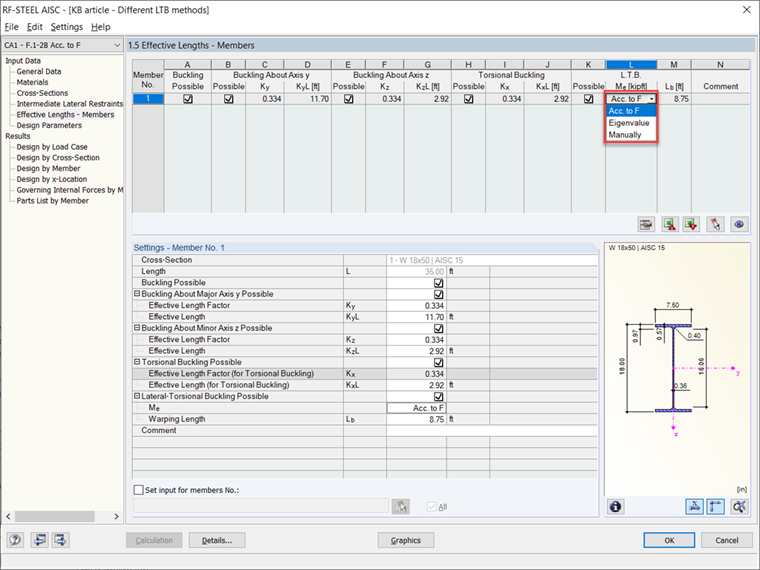
在RF-STEEL AISC附加模块中,横向扭转屈曲(LTB)在设计钢梁时默认考虑。有几种稳定性分析方法可供选择。第一种方法是根据AISC 360-16 [1]标准,使用第F章计算LTB。第二种方法是让RFEM执行特征值分析以计算主要稳定条件和弹性临界弯矩(Mcr)。这些方法都在表1.5有效长度–构件中进行,并可在下拉菜单中更改。
第F章
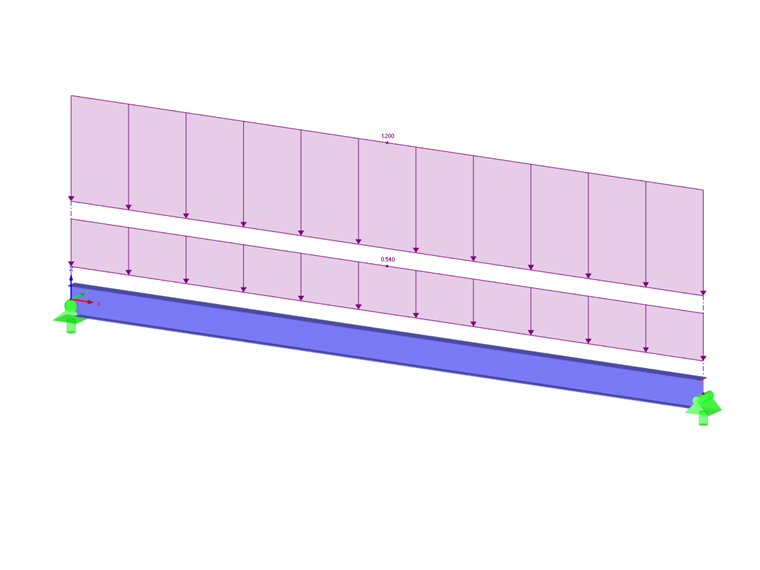
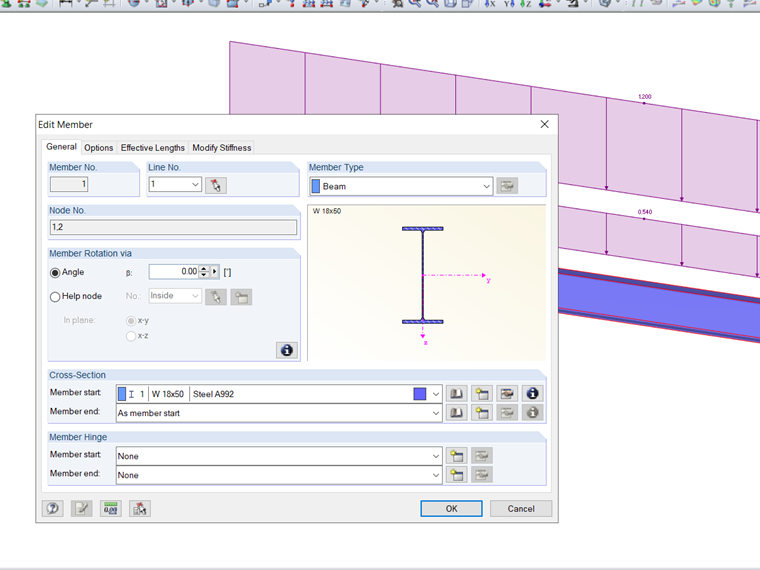
在AISC 360-16 [1]标准的第F章中,修正系数(Cb)基于跨中和四分点的最大弯矩使用公式F1-1计算。还必须计算无侧向支撑长度(Lr)和限制的无侧向支撑长度(Lp)。例如,参考取自AISC验证问题[2]的F.1-2b,一个W18X50截面包括一个施加的均匀载荷。此以及载荷条件可在图2中查看。材料为钢A992,将用于梁端部和三点的侧向约束。梁的自重将不考虑。通过下面的手算验证,RF-STEEL AISC可用于计算名义抗弯矩(Mn)。然后将此值与所需抗弯强度(Mr,y)进行比较。
首先,计算所需的抗弯强度。
Mu = (ω ⋅ L2) / 8 Mu = 266.00 kip ⋅ ft.
现在,必须为梁的中段利用公式F1-1 [1]计算横向扭转屈曲修正系数(Cb)。
|
Cb |
Lateral-torsional buckling modification factor for non-uniform moment diagrams |
|
Mmax |
Absolute value of the maximum moment in the unbraced segment |
|
MA |
Absolute value of the moment at the quarter point of the unbraced segment |
|
MB |
Absolute value of the moment at the centerline of the unbraced segment |
|
MC |
Absolute value of the moment at the three-quarter point of the unbraced segment |
Cb = 1.01
必须为端跨梁段利用公式F1-1 [1]计算横向扭转屈曲修正系数(Cb)。
Cb = 1.46
所需的较高强度和较低的Cb将起控制作用。现在,可以计算屈服极限状态的限制无侧向支撑长度(Lb)。
|
Lb |
Limiting laterally unbraced length for the limit state of yielding |
|
ry |
Radius of gyration about the y-axis |
|
E |
Modulus of elasticity |
|
Fy |
Yield strength |
Lb = 69.9 in. = 5.83 ft.
使用公式F2-6 [1]对于双对称I形构件,非弹性横向扭转屈曲极限状态的限制无支撑长度等于:
|
E |
Modulus of elasticity |
|
Fy |
Yield strength |
|
J |
Torsional constant |
|
Sx |
Elastic section modulus taken about the x-axis |
|
ho |
Distance between the flange centroids |
Lr = 203 inches
现在,必须比较弯曲屈服极限状态和非弹性横向扭转屈曲极限状态,以确定哪个起控制作用。较小的控制(Lp < Lb ≤ Lr)用于名义强度(Mn)计算。
|
Cb |
Lateral-torsional buckling modification factor for non-uniform moment diagrams |
|
Mp |
Plastic flexural strength |
|
Fy |
Yield strength |
|
Sx |
Elastic section modulus taken about the x-axis |
|
Lb |
Distance between braces |
|
Lp |
Limiting laterally unbraced length for the limit state of yielding |
|
Lr |
Limiting laterally unbraced length for the limit state of inelastic lateral-torsional buckling |
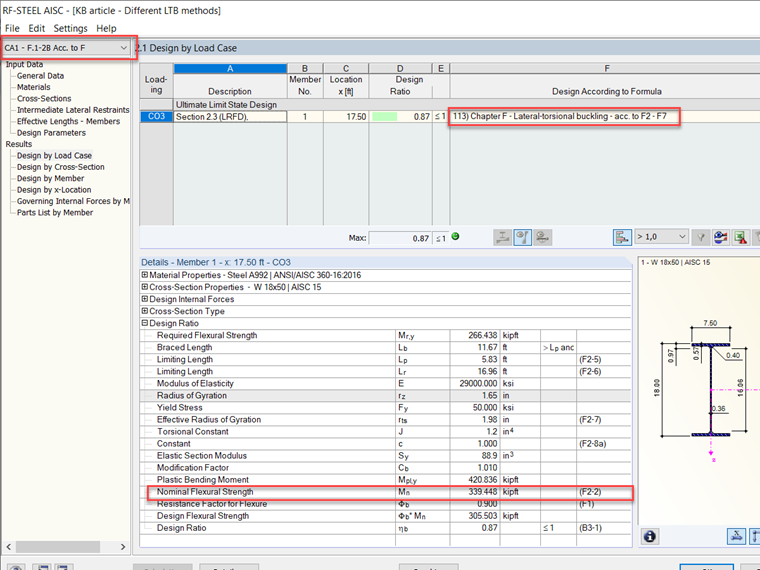
Mn = 339 kip-ft
最后,抗弯强度的阻力因子(φb)乘以Mn得出可用的抗弯强度相等于305 kip-ft。
特征值
分析LTB的第二种方法是根据特征值或Euler屈曲分析来预测弹性结构的理论屈曲强度,在这种情况下,是一个单梁构件。当发生屈曲时,使用特征值来描述载荷的值。然后使用特征向量来确定已计算特征值的形状。当结果结构刚度为零时,就会发生屈曲。在这种情况下,去除了由压缩载荷引起的应力刚度以达到弹性刚度。在大多数情况下,前几个屈曲模式最受关注。[3]
由于特征值屈曲分析是理论性的并预测弹性结构的屈曲强度,这种方法是更准确的方法,并与AISC 360-16 [1]有所不同,导致临界弯矩(Mcr)值较不保守。
比较
当比较RFEM附加模块RF-STEEL AISC与AISC 360-16 [1]的验证示例F.1-2B [2]之间的结果时,值几乎相等。结果如下比较在图4和图5中,并可以在本文下方下载模型。
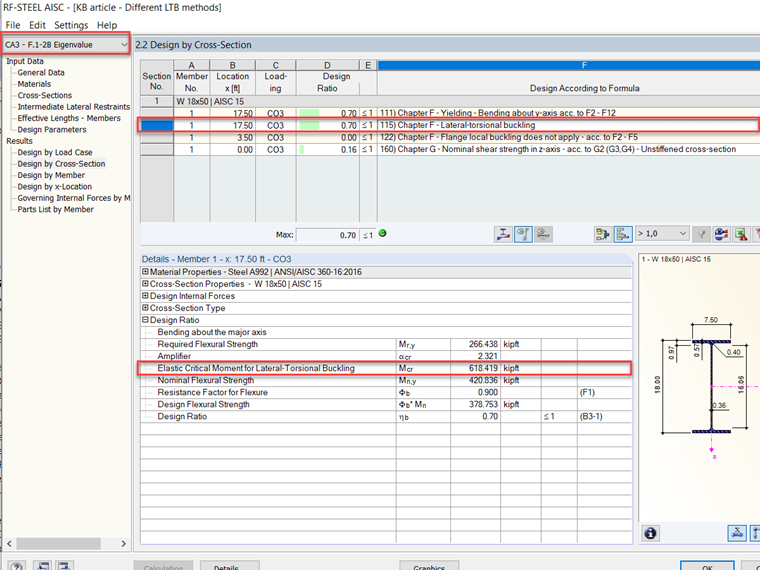
使用RF-STEEL AISC,可以运行特征值分析以计算LTB。上文提到的示例F.1-2B [2]在RFEM中建模并计算结果。您可以在图6中看到特征值分析的结果。
从AISC设计示例中计算出的相同值为: φbMn = 305 kip-ft
在RF-STEEL AISC中,根据第F章[1],计算的Mn与特征值分析中Mcr相比有所不同。从根本上说,AISC 360-16 [1]标准采用更保守的分析计算方法,而特征值分析则是一个更理论化和准确的方法。Mcr预计会是一个更大的值,而您将看到Mn不等于Mcr,因为如果LTB不起控制作用,那么Mn等于屈服或局部屈曲之间的控制值。最终,由工程师自行决定哪种方法或方法适合其构件设计。可能需要第F章的计算,但特征值分析可以从理论的角度为LTB设计提供第二种观点,以增加构件容量。
Dlubal Software网站上可以找到第F章的钢AISC验证问题,这些问题展示了手算结果与RF-STEEL AISC的结果进行对比的更多细节。这些内容可在下面链接中与模型一起获取。