Введение
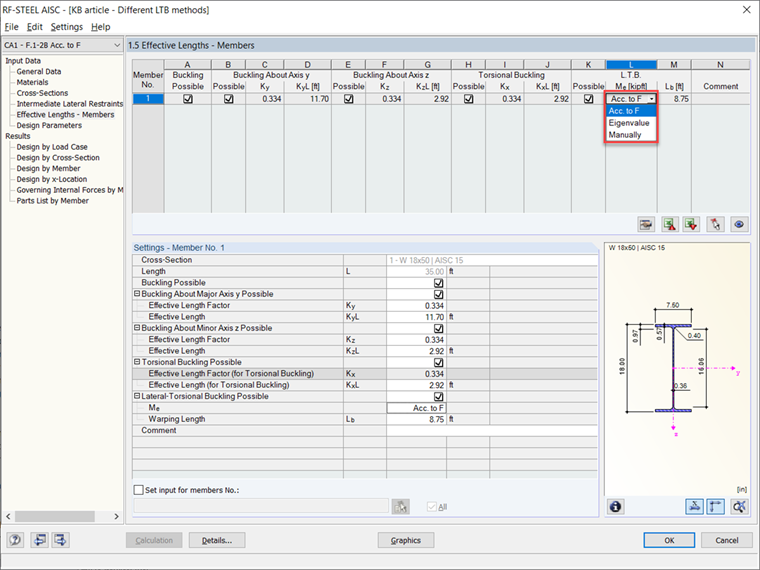
В дополнении RF-STEEL AISC, боковое кручение (LTB) учитывается по умолчанию при проектировании стальных балок. Существует несколько методов анализа устойчивости на выбор. Первый метод заключается в расчете LTB согласно стандарту AISC 360-16 [1], Глава F. Второй метод предполагает выполнение RFEM анализа собственных значений для расчета определяющих условий устойчивости и критического момента эластичности (Mcr). Эти методы осуществляются в таблице 1.5 Эффективные Длины – Элементы и могут быть изменены в выпадающем меню.
Глава F
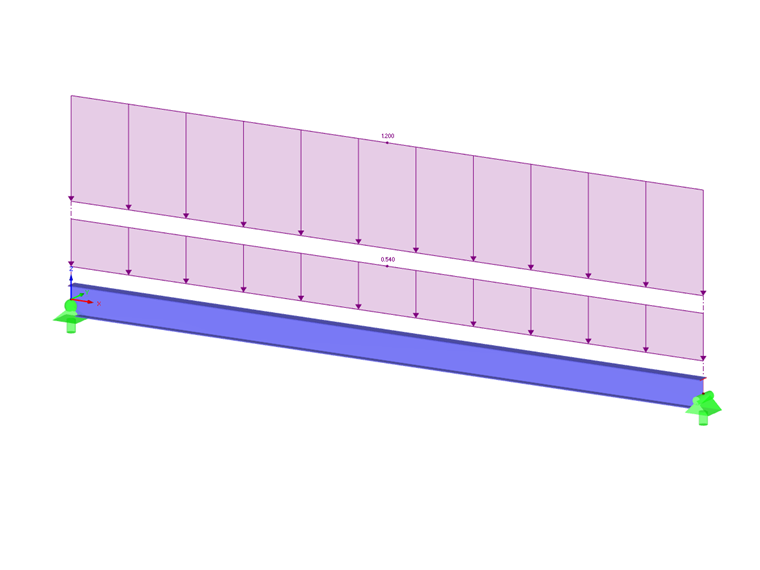
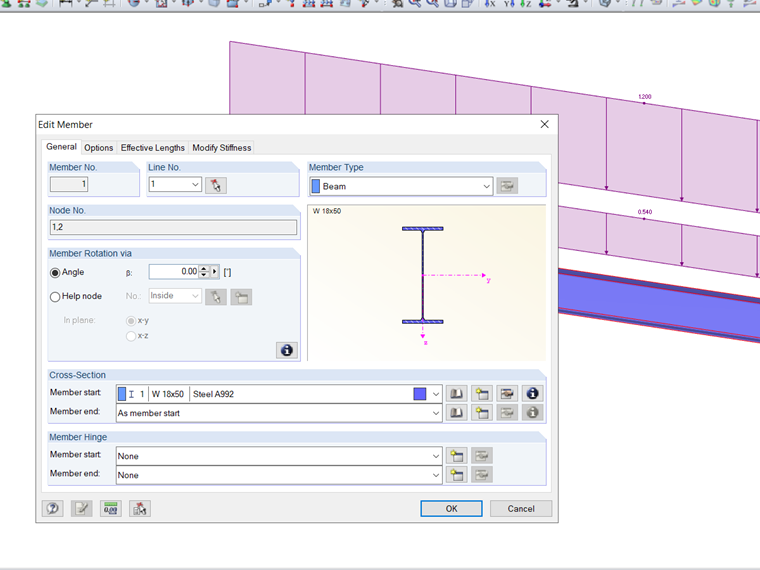
В стандарте AISC 360-16 [1], Глава F, модификационный фактор (Cb) вычисляется на основе максимального момента в середине пролета и четвертных точках вдоль балки, используя уравнение F1-1. Длина без поперечной связи (Lr) и предельная длина без поперечной связи по боковому кручению (Lp) также должны быть рассчитаны. Например, ссылаясь на F.1-2b, взятую из задач верификации AISC [2], сечение W18X50 включает приложенную равномерную нагрузку. Это, наряду с условиями нагрузки, можно увидеть на Изображении 2. Для балки будет использован материал Сталь A992, с боковыми ограничениями на концах и в третьих точках. Собственный вес балки не будет учитываться. Проверено с помощью ручных расчетов ниже, RF-STEEL AISC может быть использован для расчета номинального момента изгиба (Mn). Это значение затем сравнивается с требуемой несущей способностью изгиба (Mr,y).
Сначала рассчитывается требуемая несущая способность изгиба.
Mu = (ω ⋅ L2) / 8 Mu = 266.00 кип ⋅ фут.
Теперь необходимо рассчитать модификационный фактор по боковому кручению (Cb) для центрального сегмента балки, используя уравнение F1-1 [1].
|
Cb |
Lateral-torsional buckling modification factor for non-uniform moment diagrams |
|
Mmax |
Absolute value of the maximum moment in the unbraced segment |
|
MA |
Absolute value of the moment at the quarter point of the unbraced segment |
|
MB |
Absolute value of the moment at the centerline of the unbraced segment |
|
MC |
Absolute value of the moment at the three-quarter point of the unbraced segment |
Cb = 1.01
Модификационный фактор по боковому кручению (Cb) должен быть рассчитан для балки в конце пролета, используя уравнение F1-1 [1].
Cb = 1.46
Большее требуемое усилие и меньшее Cb будут определяющими. Теперь можно рассчитать предельную длину без поперечной связи (Lb) при предельном состоянии текучести.
|
Lb |
Limiting laterally unbraced length for the limit state of yielding |
|
ry |
Radius of gyration about the y-axis |
|
E |
Modulus of elasticity |
|
Fy |
Yield strength |
Lb = 69.9 дюймов = 5.83 фута.
Используя уравнение F2-6 [1] для симметричного I-образного элемента, предельная длина без поперечной связи при предельном состоянии неупругого бокового кручения равна:
|
E |
Modulus of elasticity |
|
Fy |
Yield strength |
|
J |
Torsional constant |
|
Sx |
Elastic section modulus taken about the x-axis |
|
ho |
Distance between the flange centroids |
Lr = 203 дюйма
Теперь необходимо сравнить предельное состояние текучести изгиба и предельное состояние неупругого бокового кручения, чтобы определить, что контролирует. Меньшее значение контролирует (Lp < Lb ≤ Lr), которое используется в расчете номинальной прочности (Mn).
|
Cb |
Lateral-torsional buckling modification factor for non-uniform moment diagrams |
|
Mp |
Plastic flexural strength |
|
Fy |
Yield strength |
|
Sx |
Elastic section modulus taken about the x-axis |
|
Lb |
Distance between braces |
|
Lp |
Limiting laterally unbraced length for the limit state of yielding |
|
Lr |
Limiting laterally unbraced length for the limit state of inelastic lateral-torsional buckling |
Mn = 339 кип-футов
Наконец, множитель сопротивления для изгибной прочности (φb) умножается на Mn, чтобы получить доступную изгибную прочность, равную 305 kip-ft.
Собственные значения
Второй метод анализа LTB основывается на анализе собственных значений или анализе Эйлера, который предсказывает теоретическую критическую прочность упругой структуры, или в данном случае отдельного элемента балки. Когда происходит потеря устойчивости, собственные значения используются для описания значений нагрузок. Затем собственные векторы используются для определения формы собственных значений, которые были рассчитаны. Когда результирующая жесткость структуры достигает нуля, происходит потеря устойчивости. Жесткость на напряжение, вызванная сжимающей нагрузкой, удаляется из упругой жесткости в этом сценарии. В большинстве обстоятельств первые несколько режимов потери устойчивости являются наиболее интересными. [3]
Поскольку анализ на собственные значения является теоретическим и предсказывает критическую прочность упругой структуры, этот метод является более точным и отличается от AISC 360-16 [1], приводя к менее консервативному значению критического момента (Mcr).
Сравнение
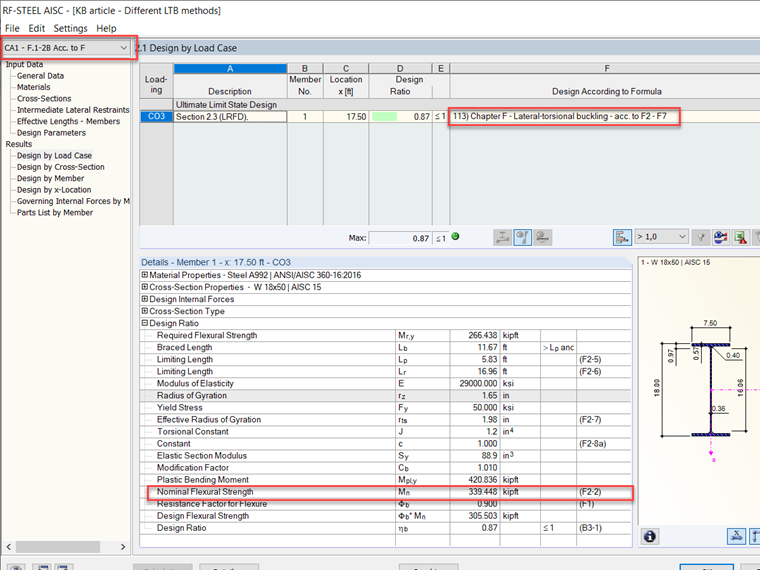
При сравнении результатов между дополнением RFEM RF-STEEL AISC и примером верификации F.1-2B [2] из AISC 360-16 [1], значения почти полностью совпадают. Результаты сравниваются ниже на изображениях 4 и 5, а модель можно скачать ниже этой статьи.
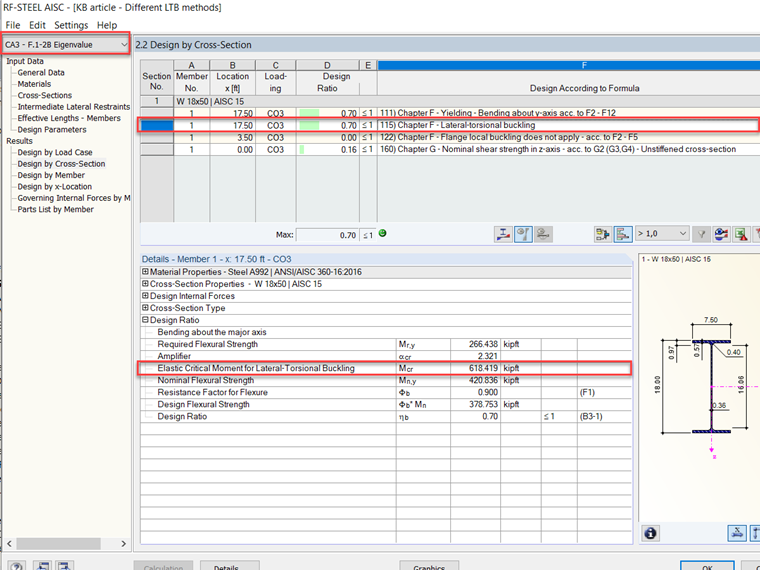
С RF-STEEL AISC возможно выполнить анализ на собственные значения для расчета LTB. Пример F.1-2B [2], упомянутый выше, был смоделирован в RFEM, и результаты были рассчитаны. Вы можете увидеть результаты анализа собственных значений на изображении 6.
То же значение, рассчитанное из примеров проектирования AISC, составило: φbMn = 305 кип-футов
Mn, согласно Главе F [1] в RF-STEEL AISC, варьируется в сравнении с Mcr из анализа собственных значений. Фундаментально, стандарт AISC 360-16 [1] занимает более консервативный подход с аналитическими расчетами по сравнению с анализом собственных значений, который является более теоретическим и точным подходом. Ожидается, что Mcr будет большим значением, и вы увидите, что Mn не равен Mcr, потому что если LTB не контролирует, то Mn равен контролирующему значению между текучестью или локальной потерей устойчивости. В конечном счете, это остается на усмотрение инженера, какой метод или подход подходит для их проектирования элемента. Вероятно, что расчеты по Главе F требуются, но анализ собственных значений может предоставить второй взгляд на проектирование LTB с точки зрения теории для дополнительной несущей способности элемента.
Задачи верификации стали AISC из Главы F можно найти на веб-сайте Dlubal Software, где показаны более подробные сравнения ручных расчетов с результатами в RF-STEEL AISC. Они доступны по ссылке ниже вместе с моделью.