Wprowadzenie
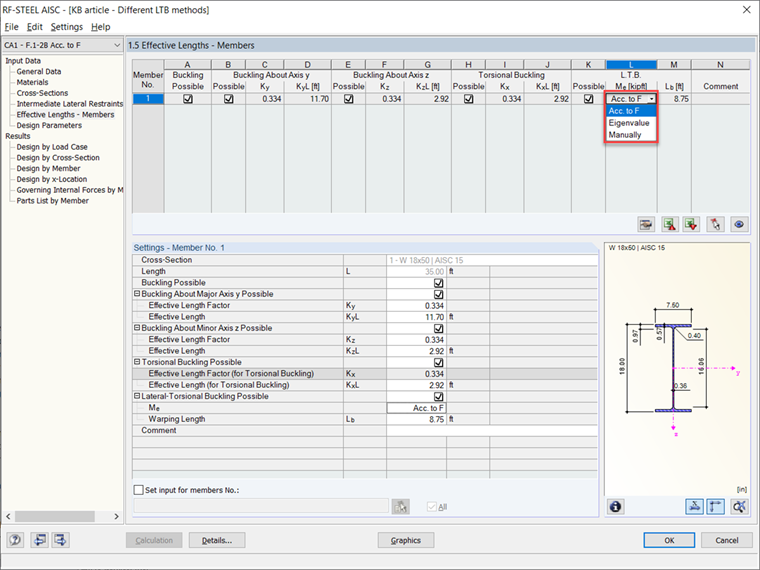
W module dodatkowym RF-STEEL AISC wyboczenie skrętne boczne (LTB) jest domyślnie uwzględniane podczas projektowania belek stalowych. Istnieje kilka metod analizy stateczności do wyboru. Pierwsza metoda polega na obliczaniu LTB zgodnie z normą AISC 360-16 [1], Rozdział F. Druga metoda polega na tym, że RFEM wykonuje analizę wartości własnych, aby obliczyć dominujące warunki stateczności i elastyczny moment krytyczny (Mcr). Wszystkie te metody odbywają się w Tabeli 1.5 Długości Efektywne – Elementy i mogą być zmieniane w menu rozwijanym.
Rozdział F
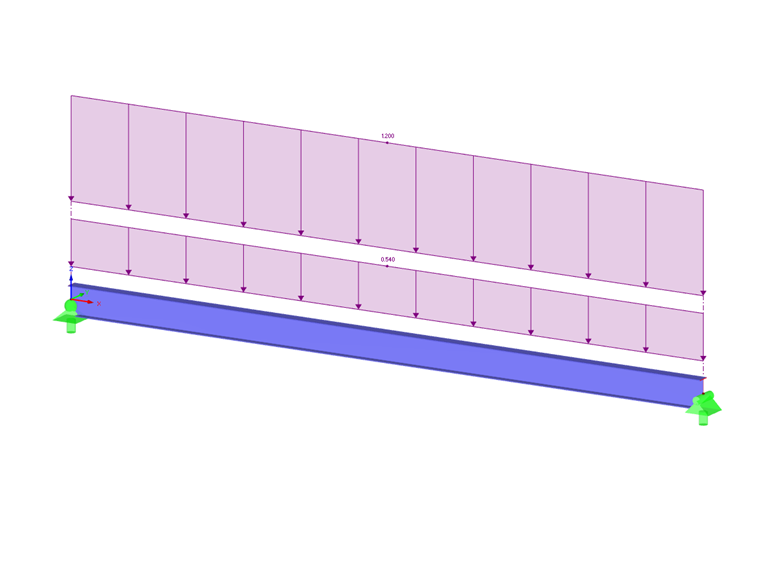
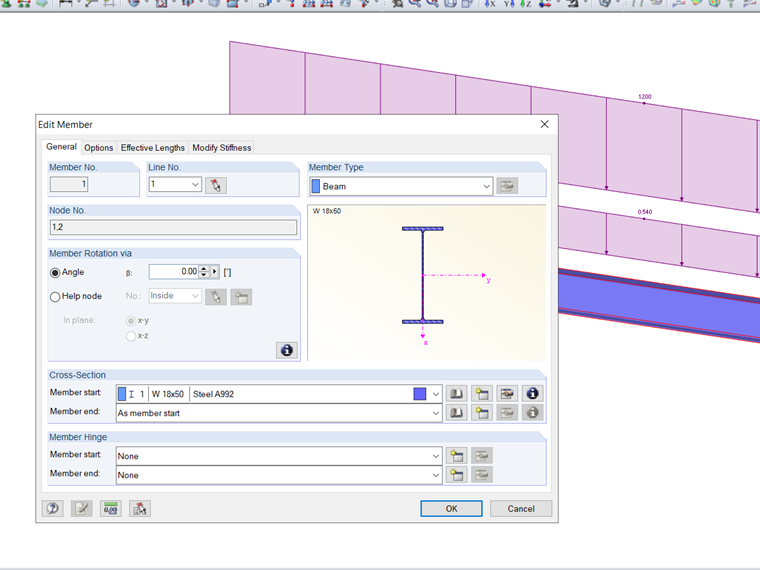
W normie AISC 360-16 [1], Rozdział F, współczynnik modyfikujący (Cb) obliczany jest na podstawie maksymalnego momentu w środkowej i ćwiartkowej części belki, wykorzystując równanie F1-1. Trzeba również obliczyć długość nieprzelotową (Lr) i ograniczającą bocznie nieprzelotową długość (Lp). Na przykład, odnosząc się do F.1-2b zaczerpniętego z problemów weryfikacyjnych AISC [2], przekrój W18X50 zawiera przyłożone równomierne obciążenie. To, wraz z kryteriami obciążenia, można zobaczyć na Obraz 2. Materiał, Stal A992, zostanie użyty dla belki wraz z bocznymi ograniczeniami na końcach i w trzecich punktach. Własna masa belki nie będzie uwzględniana. Zweryfikowane poniżej obliczenia ręczne, RF-STEEL AISC można użyć do obliczenia nominalnego momentu zginającego (Mn). Ta wartość jest następnie porównywana z wymaganym momentem zginającym (Mr,y).
Najpierw obliczany jest wymagany moment zginający.
Mu = (ω ⋅ L2) / 8 Mu = 266.00 kip ⋅ ft.
Teraz należy obliczyć współczynnik modyfikacji wyboczenia skrętnego bocznego (Cb) dla środkowego segmentu belki, wykorzystując równanie F1-1 [1].
|
Cb |
Lateral-torsional buckling modification factor for non-uniform moment diagrams |
|
Mmax |
Absolute value of the maximum moment in the unbraced segment |
|
MA |
Absolute value of the moment at the quarter point of the unbraced segment |
|
MB |
Absolute value of the moment at the centerline of the unbraced segment |
|
MC |
Absolute value of the moment at the three-quarter point of the unbraced segment |
Cb = 1.01
Należy obliczyć współczynnik modyfikacji wyboczenia skrętnego bocznego (Cb) dla belki końcowego przęsła, wykorzystując równanie F1-1 [1].
Cb = 1.46
Wyższa wymagana wytrzymałość i niższe Cb będą decydować. Teraz można obliczyć ograniczającą bocznie nieprzelotową długość (Lb) dla stanu granicznego płynięcia.
|
Lb |
Limiting laterally unbraced length for the limit state of yielding |
|
ry |
Radius of gyration about the y-axis |
|
E |
Modulus of elasticity |
|
Fy |
Yield strength |
Lb = 69.9 in. = 5.83 ft.
Korzystając z równania F2-6 [1] dla członu kształtowanego symetrycznie, ograniczającą długość boczną dla stanu granicznego nieelastycznego wyboczenia skrętnego bocznego równa się:
|
E |
Modulus of elasticity |
|
Fy |
Yield strength |
|
J |
Torsional constant |
|
Sx |
Elastic section modulus taken about the x-axis |
|
ho |
Distance between the flange centroids |
Lr = 203 inches
Teraz należy porównać stan graniczny płynięcia z momentem zginającym i stan graniczny nieelastycznego wyboczenia skrętnego bocznego, aby określić, który kontroluje. Mniejszy kontroluje (Lp < Lb ≤ Lr), co jest używane w obliczeniu nominalnej wytrzymałości (Mn).
|
Cb |
Lateral-torsional buckling modification factor for non-uniform moment diagrams |
|
Mp |
Plastic flexural strength |
|
Fy |
Yield strength |
|
Sx |
Elastic section modulus taken about the x-axis |
|
Lb |
Distance between braces |
|
Lp |
Limiting laterally unbraced length for the limit state of yielding |
|
Lr |
Limiting laterally unbraced length for the limit state of inelastic lateral-torsional buckling |
Mn = 339 kip-ft
Na koniec współczynnik odporności na wytrzymałość zginającą (φb) jest mnożony przez Mn, aby dać dostępną wytrzymałość zginającą równą 305 kip-ft.
Wartość własna
Drugą metodą analizy LTB jest analiza wg wartości własnej lub analiza wyboczeniowa Eulera, która przewiduje teoretyczną wytrzymałość wyboczeniową elastycznej struktury, lub w tym przypadku, pojedyńczego elementu belkowego. Kiedy wstępuje wyboczenie, wartości własne są używane do opisania wartości obciążeń. Następnie wektory własne są używane do określenia kształtu wartości własnych, które zostały obliczone. Gdy sztywność struktury osiąga zero, następuje wyboczenie. Sztywność naprężeniowa wywołana obciążeniem ściskającym jest odejmowana od sztywności elastycznej w tym scenariuszu. W większości przypadków największe zainteresowanie budzą pierwsze kilka modów wyboczenia. [3]
Ponieważ analiza wyboczenia wg wartości własnej jest teoretyczna i przewiduje wytrzymałość wyboczeniową struktury elastycznej, ta metoda jest bardziej dokładnym podejściem i różni się od normy AISC 360-16 [1], prowadząc do mniej konserwatywnej wartości momentu krytycznego (Mcr).
Porównanie
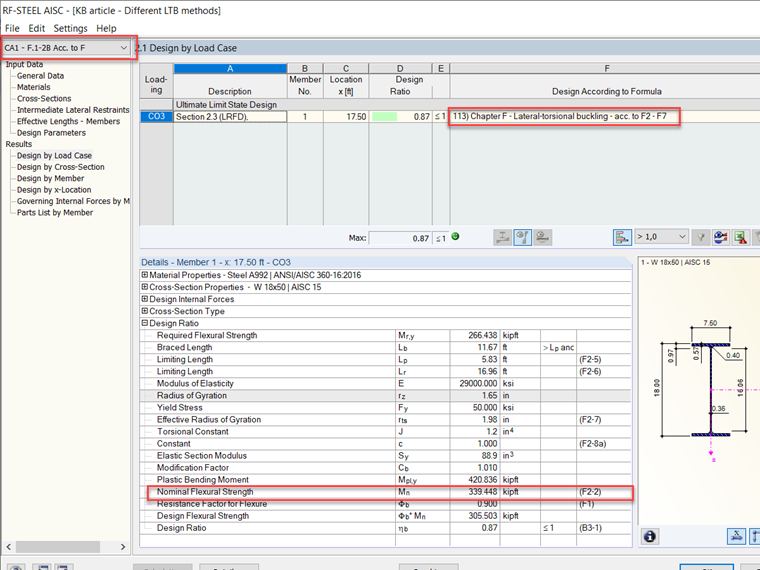
Porównując wyniki między modułem dodatkowym RF-STEEL AISC a przykładem weryfikacyjnym F.1-2B [2] z normy AISC 360-16 [1], wartości są niemal dokładne. Wyniki są porównywane poniżej na Obrazach 4 i 5, a model można pobrać poniżej tego artykułu.
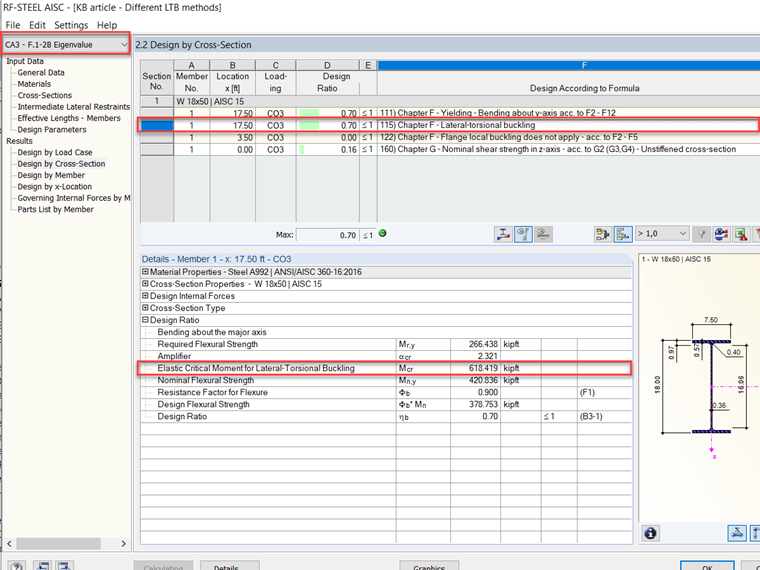
Za pomocą RF-STEEL AISC można przeprowadzić analizę wartości własnej w celu obliczenia LTB. Przykład F.1-2B [2], o którym mowa powyżej, został wymodelowany w RFEM, a wyniki zostały obliczone. Możesz zobaczyć wyniki z analizy wartości własnej na Obrazie 6.
Ta sama wartość obliczona z Przykładów Projektowych AISC wyniosła: φbMn = 305 kip-ft
Mn zgodnie z Rozdziałem F [1] w RF-STEEL AISC różni się, gdy porównać do Mcr z analizy wartości własnej. Fundamentalnie, norma AISC 360-16 [1] adoptuje bardziej konserwatywne podejście z obliczeniami analitycznymi w porównaniu do analizy wartości własnej, która jest bardziej teoretyczna i dokładna. Oczekuje się, że Mcr będzie większą wartością, a zobaczysz, że Mn nie jest równy Mcr, ponieważ jeśli LTB nie kontroluje, to Mn jest równy wartości decydującej między płynięciem a lokalnym wyboczeniem. Ostatecznie, to inżynier decyduje, która metoda lub podejście jest odpowiednie do projektowania danego elementu. Obliczenia zgodnie z Rozdziałem F są prawdopodobnie wymagane, ale analiza wartości własnej może dostarczyć drugiego spojrzenia na projektowanie LTB z teoretycznego punktu widzenia dla dodatkowej nośności elementu.
Problemy weryfikacyjne AISC ze Stali z Rozdziału F można znaleźć na stronie internetowej Dlubal Software, gdzie pokazane są bardziej szczegółowe porównania ręcznych obliczeń do wyników w RF-STEEL AISC. Są one dostępne w linku poniżej wraz z modelem.