Úvod
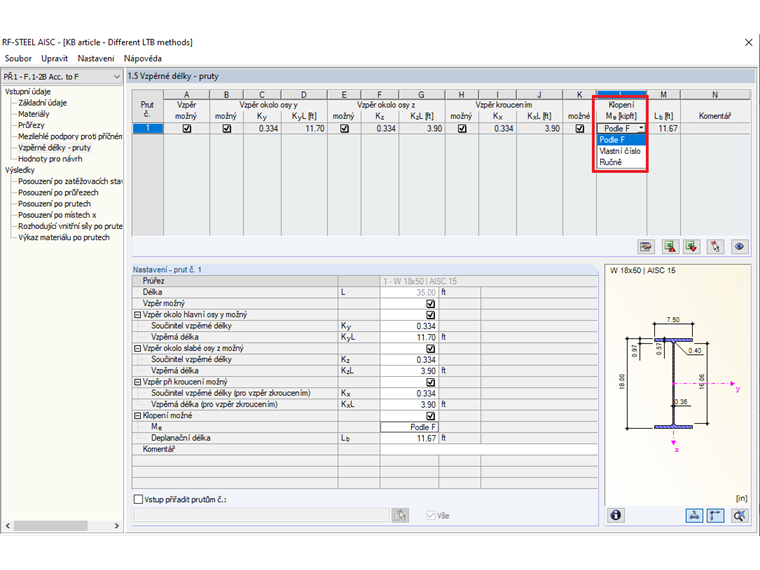
V přídavném modulu RF-STEEL AISC se klopení (LTB) při posouzení ocelových nosníků automaticky uvažuje. K dispozici je několik metod analýzy stability. První metodou je výpočet klopení podle normy AISC 360-16 [1], kapitoly F. Druhou metodou je nechat v programu RFEM provést analýzu vlastních čísel pro výpočet rozhodujících podmínek stability a pružného kritického momentu (Mcr). Všechny tyto metody nabízí tabulka 1.5 Vzpěrné délky - pruty a lze je vybrat v rozbalovací nabídce.
Kapitola F
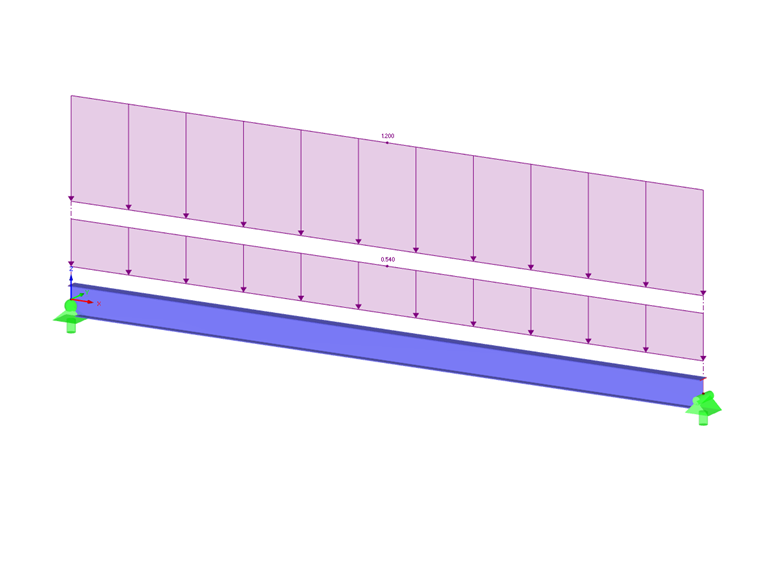
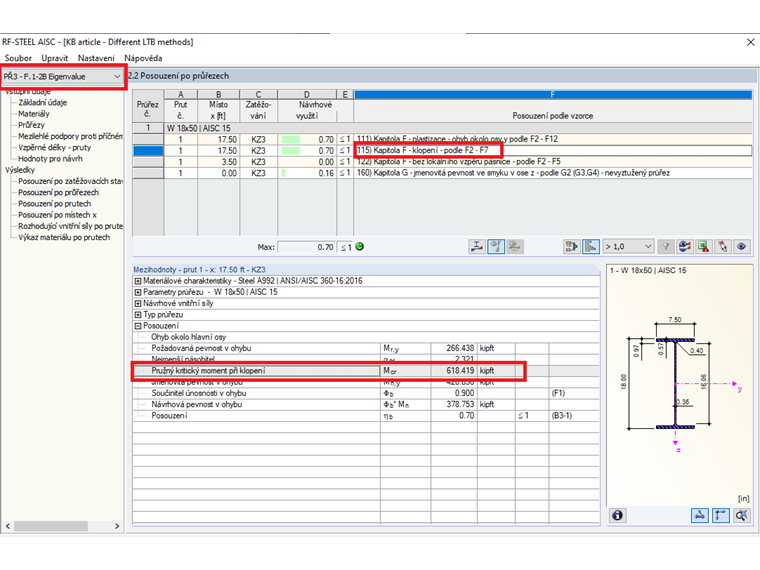
V normě AISC 360-16 [1], kapitole F, se modifikační součinitel (Cb) počítá na základě maximálního momentu ve středním a čtvrtinových bodech podél nosníku pomocí rovnice F1-1. Je třeba rovněž spočítat nevyztuženou délku (Lr) a mezní bočně nevyztuženou délku (Lp). Například, podle F.1-2b z Verifikačních příkladů AISC [2], uvažujme nosník s průřezem W18X50, na nějž působí rovnoměrné zatížení. Ten, spolu s kritérii zatížení, vidíme na Obrázku 2. Materiál nosníku bude ocel A992, podél nosníku budou příčné podpory na koncích a ve třetinách délky. Vlastní tíha nosníku nebude zohledněna. Jak je ověřeno ručním výpočtem níže, RF-STEEL AISC lze použít pro výpočet jmenovitého ohybového momentu (Mn). Tato hodnota se pak porovná s požadovanou pevností v ohybu (Mr,y).
Nejdříve se spočítá požadovaná pevnost v ohybu.
Mu = (ω ⋅ L2) / 8
Mu = 266,00 kip ⋅ ft.
Nyní je třeba vypočítat modifikační součinitel klopení (Cb) pro středový segment nosníku pomocí rovnice F1-1 [1].
| Cb | Modifikační součinitel klopení pro nerovnoměrné průběhy momentů |
| Mmax | Absolutní hodnota maximálního momentu v nevyztuženém segmentu |
| MA | Absolutní hodnota momentu ve čtvrtině nevyztuženého segmentu |
| MB | Absolutní hodnota momentu ve střednici nevyztuženého segmentu |
| MC | Absolutní hodnota momentu v bodě tří čtvrtin nevyztuženého segmentu |
Cb = 1,01
Modifikační součinitel klopení (Cb) je třeba vypočítat pro krajní segmenty nosníku pomocí rovnice F1-1 [1].
Cb = 1,46
Rozhodující je vyšší požadovaná pevnost a nižší Cb. Nyní můžeme vypočítat mezní bočně nevyztuženou délku pro mezní stav plastizace (Lb).
| Lb | Mezní bočně nevyztužená délka pro mezní stav plastizace |
| ry | Poloměr setrvačnosti okolo osy y |
| E | Modul pružnosti |
| Fy | Mez kluzu |
Lb = 69,9 in. = 5,83 ft.
Podle rovnice F2-6 [1] pro dvojitě symetrický prut s I-průřezem se mezní nevyztužená délka pro mezní stav neelastického klopení rovná:
| E | Modul pružnosti |
| Fy | Mez kluzu |
| J | Moment setrvačnosti v kroucení |
| Sx | Elastický průřezový modul okolo osy x |
| ho | Vzdálenost mezi středy pásnic |
Lr = 203 in
Nyní je třeba porovnat mezní stav plastizace v ohybu s neelastickým mezním stavem klopení, abychom určili, který je rozhodující. Menší (Lp <Lb ≤ Lr) se použije při výpočtu jmenovité pevnosti v ohybu (Mn).
| Cb | Modifikační součinitel klopení pro nerovnoměrné průběhy momentů |
| Mp | Plastická pevnost v ohybu |
| Fy | Mez kluzu |
| Sx | Elastický průřezový modul okolo osy x |
| Lb | Vzdálenost mezi ztužidly |
| Lp | Mezní bočně nevyztužená délka pro mezní stav plastizace |
| Lr |
Mezní bočně nevyztužená délka pro mezní stav nepružného klopení |
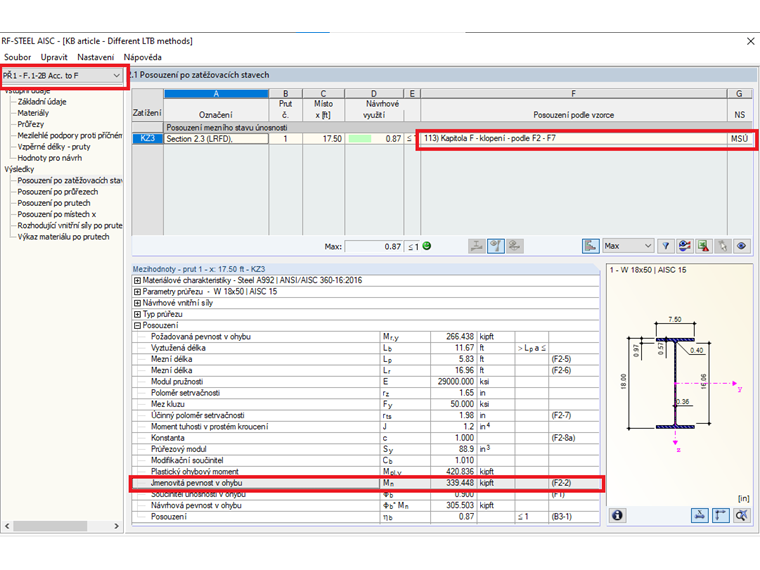
Mn = 339 kip-ft
Nakonec se součinitel únosnosti v ohybu (φb) vynásobí Mn, čímž získáme návrhovou pevnost v ohybu 305 kip-ft.
Vlastní číslo
Druhá metoda výpočtu pro posouzení klopení je pomocí vlastního čísla nebo-li Eulerovy analýzy vzpěru, která předpovídá teoretickou vzpěrnou pevnost pružné konstrukce, nebo v tomto případě jednoho prutu. V případě vzpěru se k popisu hodnot zatížení používají vlastní čísla. Poté se pomocí vlastních tvarů stanoví tvar vybočení pro vlastní čísla, která byla spočítána. Jakmile výsledná tuhost konstrukce dosáhne nuly, dojde k vybočení. Napěťová tuhost způsobená tlakovým zatížením se pro tento případ z pružné tuhosti odstraní. Ve většině případů je několik prvních tvarů boulení nejzajímavějších. [3]
Vzhledem k tomu, že analýza vzpěru pomocí vlastních čísel je teoretická a předpovídá vzpěrnou pevnost pružné konstrukce, je tato metoda přesnější a liší se od AISC 360-16 [1], což vede k méně konzervativní hodnotě kritického momentu (Mcr).
Porovnání
Při porovnání výsledků z přídavného modulu RF-STEEL AISC a verifikačním příkladem F.1-2B [2] z AISC 360-16 [1] jsou hodnoty téměř přesné. Výsledky jsou porovnány níže na obrázcích 4 a 5 a model lze stáhnout pomocí odkazu pod tímto článkem.
S přídavným modulem RF-STEEL AISC lze provést analýzu vlastních čísel pro výpočet klopení. Příklad F.1-2B [2], na který odkazujeme výše, byl namodelován v programu RFEM a byly spočítány výsledky. Na obrázku 6 vidíme výsledky analýzy vlastních čísel.
Vyšla stejná hodnota jako ta vypočítaná z návrhových příkladů AISC:
φbMn = 305 kip-ft
Mn podle kapitoly F [1] v modulu RF-STEEL AISC se liší od Mcr z analýzy vlastních čísel. Norma AISC 360-16 [1] je v zásadě konzervativnější při analytických výpočtech ve srovnání s analýzou vlastních čísel, která je teoretičtější a přesnější. Podle očekávání bude mít Mcr větší hodnotu a uvidíme, že Mn se nerovná Mcr, protože pokud klopení není rozhodující, pak se Mn rovná rozhodující hodnotě buď z plastizace, nebo lokálního boulení. Nakonec záleží na uvážení inženýra, který způsob nebo postup vybere jako vhodný pro návrh prutu. Výpočty podle kapitoly F budou pravděpodobně požadovány, ale analýza vlastních čísel může poskytnout bližší pohled na posouzení klopení z teoretického hlediska pro větší únosnost prutu.
Verifikační příklad posouzení oceli podle AISC, kapitoly F, lze najít na webových stránkách společnosti Dlubal Software, kde jsou uvedeny další podrobnosti při porovnání ručních výpočtů s výsledky v modulu RF-STEEL AISC. Ty jsou k dispozici v níže uvedeném odkazu s modelem.
.jpg?mw=350&hash=91f398b559b26a6ac36fd7ecdf5e395e7b9b856d)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
