Introducción
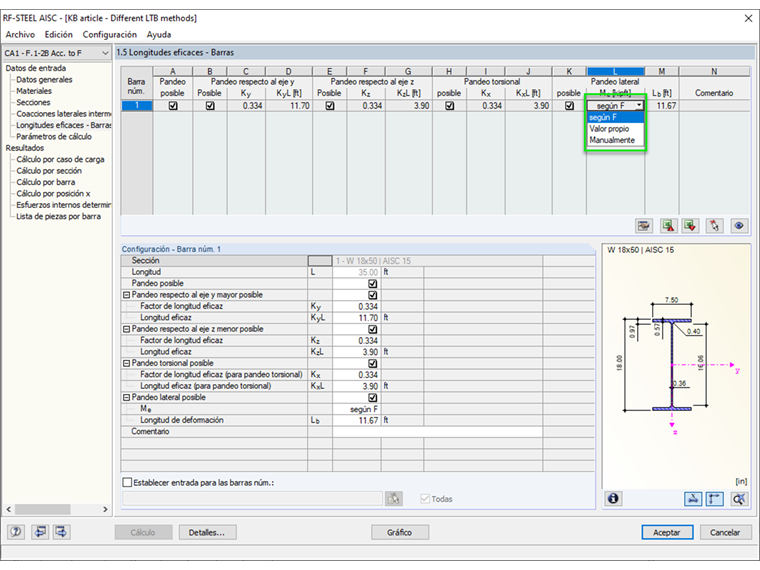
Dentro del módulo adicional RF-STEEL AISC, se considera el pandeo lateral-torsional (LTB) por defecto al calcular vigas de acero. Puede elegir entre un par de métodos de análisis de estabilidad. El primer método es calcular el pandeo lateral según la norma AISC 360-16 [1], capítulo F. El segundo método es hacer que RFEM realice un análisis de valores propios para calcular las condiciones de estabilidad determinantes y el momento crítico elástico (Mcr). Todos estos métodos tienen lugar en la Tabla 1.5 Longitudes eficaces - Barras y se pueden cambiar en el menú desplegable.
Capítulo F
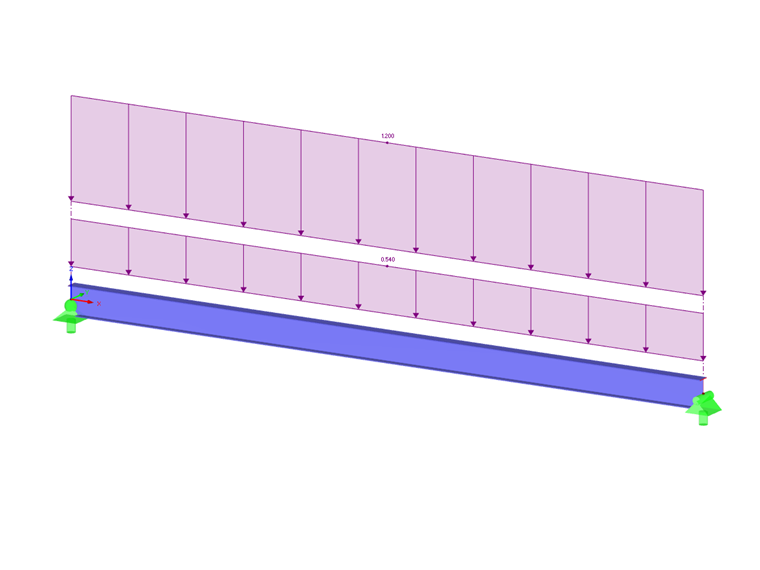
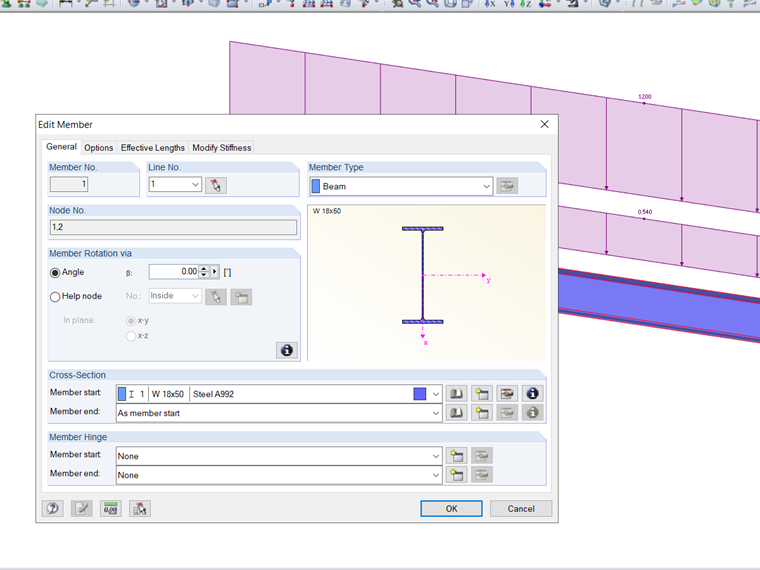
En la norma AISC 360-16 [1], capítulo F, el factor de modificación (Cb ) se calcula sobre la base del momento máximo en el punto medio del vano y en un cuarto a lo largo de la viga utilizando Ec. F1-1. También se debe calcular la longitud no arriostrada (Lr) y la longitud límite no arriostrada lateralmente (Lp). Por ejemplo, en referencia a F.1-2b tomado de los problemas de verificación de AISC [2], una sección W18X50 incluye una carga uniforme aplicada. Esto, junto con los criterios de carga, se puede ver en la Imagen 2. El material, Acero A992, se utilizará para la viga junto con las coacciones laterales en los extremos y puntos en los tercios. No se considera el peso propio de la viga. Verificado con los cálculos manuales a continuación, RF-STEEL AISC se puede usar para calcular la resistencia nominal a flexión (Mn). Este valor se compara luego con la resistencia necesaria a flexión (Mr,y).
Primero, se calcula la resistencia necesaria a flexión.
Mu = (ω ⋅ L2 ) / 8
Mu = 266,00 kip ⋅ ft
Ahora, se debe calcular el factor de modificación de pandeo lateral (Cb ) para el segmento central de la viga utilizando la ecuación F1-1 [1].
| Cb | Factor de modificación del pandeo lateral-torsional para diagramas de momento no uniformes |
| Mmáx. | Valor absoluto del momento máximo en el segmento sin arriostrar |
| MA | Valor absoluto del momento en el cuarto de punto del segmento sin arriostrar |
| MB | Valor absoluto del momento en la línea central del segmento sin arriostrar |
| MC | Valor absoluto del momento en el punto tres cuartos del segmento sin arriostrar |
Cb = 1,01
El factor de modificación de pandeo lateral (Cb ) se debe calcular para la viga de vano final utilizando la ecuación F1-1 [1].
Cb = 1,46
La mayor resistencia requerida y el menor Cb serán los determinantes. Ahora se puede calcular la longitud límite sin arriostrar lateralmente (Lb) para el estado límite de fluencia.
| Lb | Longitud límite lateral sin arriostrar para el estado límite de fluencia |
| ry | Radio de giro respecto al eje y |
| E | Módulo de elasticidad |
| Fy | Límite elástico |
Lb = 69,9 in = 5,83 ft
Usando la ecuación F2-6 [1] para una barra en I de simetría doble, la longitud límite sin arriostrar para el estado límite de pandeo lateral inelástico es igual a:
| E | Módulo de elasticidad |
| Fy | límite elástico |
| J | Módulo de torsión |
| Sx | Módulo resistente elástico de la sección respecto al eje x |
| ho | Distancia entre centros de gravedad de alas |
Lr = 203 pulgadas
Ahora, el estado límite de fluencia por flexión y el estado límite de pandeo lateral inelástico se deben comparar para determinar cuál está controlando. Los valores de control menores (Lp <Lb ≤ Lr ) se utilizan en el cálculo de la resistencia nominal (Mn).
| Cb | Factor de modificación del pandeo lateral-torsional para diagramas de momento no uniformes |
| Mp | Resistencia a flexión plástica |
| Fy | límite elástico |
| [SCHOOL.PHONE]x | Módulo resistente elástico de la sección respecto al eje x |
| Lb | Distancia entre arriostramientos |
| Lp | Longitud límite lateral sin arriostrar para el estado límite de fluencia |
| Lr |
Longitud límite sin arriostrar lateralmente para el estado límite de pandeo lateral inelástico |
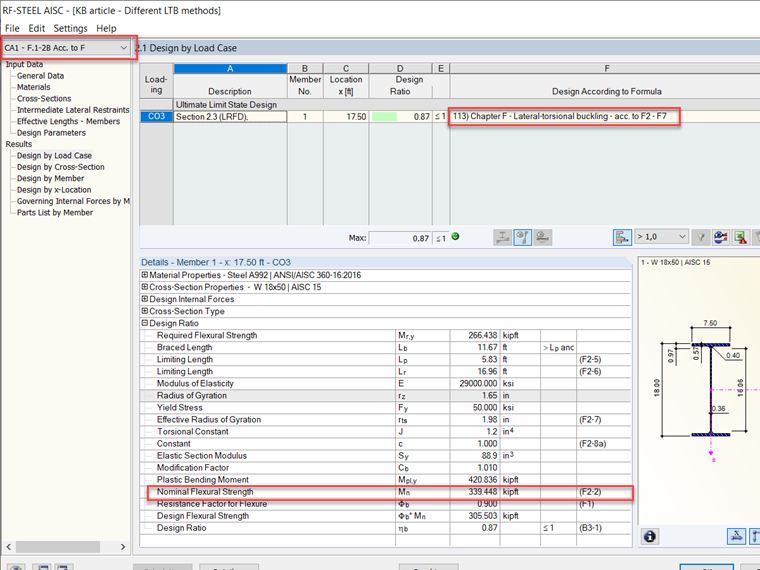
Mn = 339 kip-ft
Por último, el factor de resistencia para la resistencia a flexión (φb ) se multiplica por Mn para dar la resistencia a flexión disponible igual a 305 kip-ft.
Valores propios
El segundo método de análisis para analizar la pandeo lateral es según un valor propio o análisis de pandeo de Euler que predice la resistencia teórica al pandeo de una estructura elástica, o en este caso, una barra simple. Cuando se produce el pandeo, se utilizan los valores propios para describir los valores de las cargas. Luego, los vectores propios se utilizan para determinar la forma de los valores propios que se calcularon. Cuando la rigidez de la estructura resultante llega a cero, se produce el pandeo. La rigidez a la tensión causada por una carga de compresión se elimina de la rigidez elástica para esta situación. En la mayoría de las circunstancias, los primeros modos de pandeo son los de mayor interés. [3]
Dado que un análisis de pandeo por valores propios es teórico y predice la resistencia al pandeo de una estructura elástica, este método es un enfoque más exacto y difiere de la norma AISC 360-16 [1] que conduce a un enfoque menos conservador valor del momento crítico (Mcr ).
Comparación
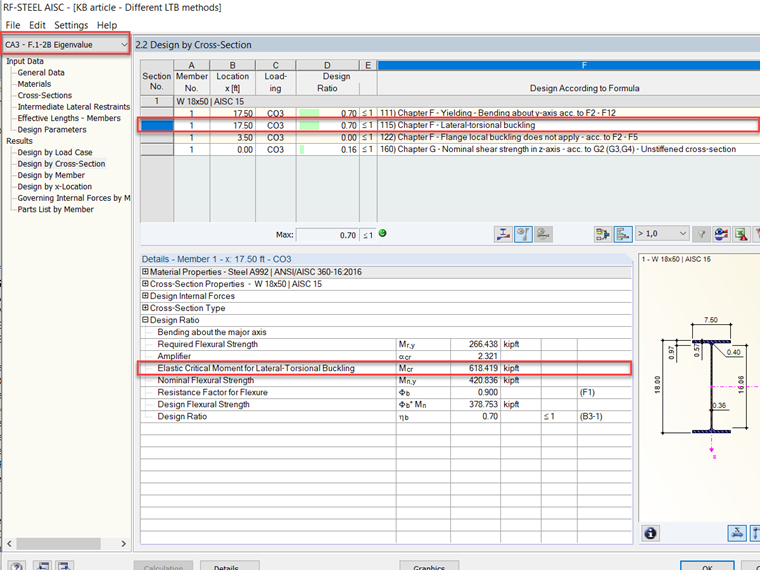
Al comparar los resultados entre el módulo adicional RF-STEEL AISC de RFEM y el ejemplo de verificación F.1-2B [2] de AISC 360-16 [ 1], los valores son casi exactos. Los resultados se comparan a continuación en las imágenes 4 y 5, y el modelo se puede descargar debajo de este artículo.
Con RF-STEEL AISC, es posible realizar un análisis de valores propios para calcular el pandeo lateral-torsional. El ejemplo F.1-2B [2], mencionado anteriormente, se modeló en RFEM y se calcularon los resultados. Puede ver en la Imagen 6 los resultados del análisis de valores propios.
El mismo valor calculado a partir de los ejemplos de diseño de AISC resultó como:
φb Mn = 305 kip-ft
Mn según el capítulo F [[#Refer [1{%\} ] en RF-STEEL AISC varía en comparación conMcr de un análisis de valores propios. Fundamentalmente, la norma AISC 360-16 [1] adopta un enfoque más conservador con cálculos analíticos en comparación con un análisis de valores propios, que es un enfoque más teórico y exacto. Se espera queMcr sea un valor mayor, y verá queMn no es igual a Mcrporque si el pandeo lateral no está controlando, entoncesMn es igual al valor de control entre la fluencia o el pandeo local. En última instancia, queda a discreción del ingeniero' qué método o enfoque es adecuado para el cálculo de su barra. Es probable que se necesiten los cálculos del capítulo F, pero un análisis de valores propios puede proporcionar una segunda mirada al cálculo de pandeo lateral desde un punto de vista teórico para la capacidad adicional de la barra.
Los problemas de verificación del acero AISC del capítulo F se pueden encontrar en el sitio web de Dlubal Software', donde se muestran más detalles comparando los cálculos manuales con los resultados en RF-STEEL AISC. Estos están disponibles en el siguiente enlace con el modelo.
