AISC Chapter F Lateral Torsional Buckling Versus Eigenvalue Calculation Methods Compared
Technical Article
Utilizing the RF-STEEL AISC add-on module, steel member design is possible according to the AISC 360-16 standard. The following article will compare the results between calculating lateral torsional buckling according to Chapter F and Eigenvalue Analysis.
Introduction
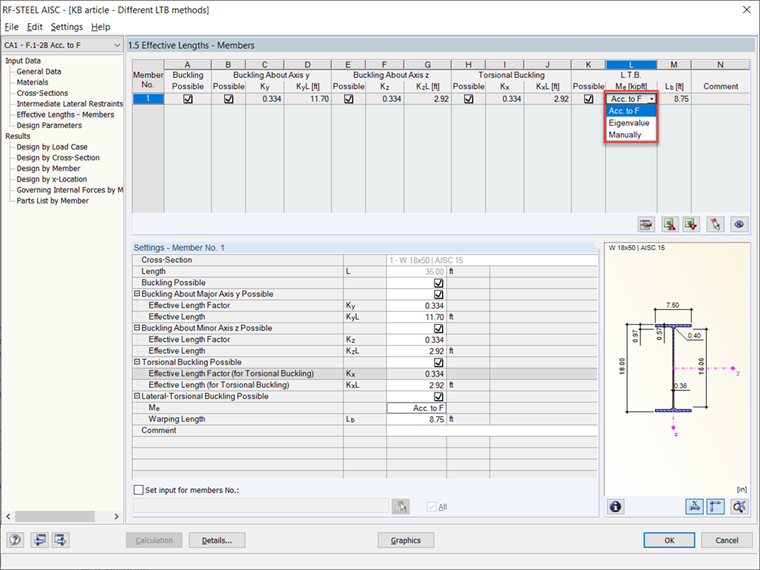
Within the RF-STEEL AISC add-on module, lateral-torsional buckling (LTB) by default is considered when designing steel beams. There are a couple of stability analysis methods to choose from. The first method is to calculate LTB according to the AISC 360-16 [1] standard, Chapter F. The second method is to have RFEM perform an eigenvalue analysis to calculate the governing stability conditions and the elastic critical moment (Mcr). These methods all take place in Table 1.5 Effective Lengths - Members and can be changed within the dropdown menu.
Chapter F
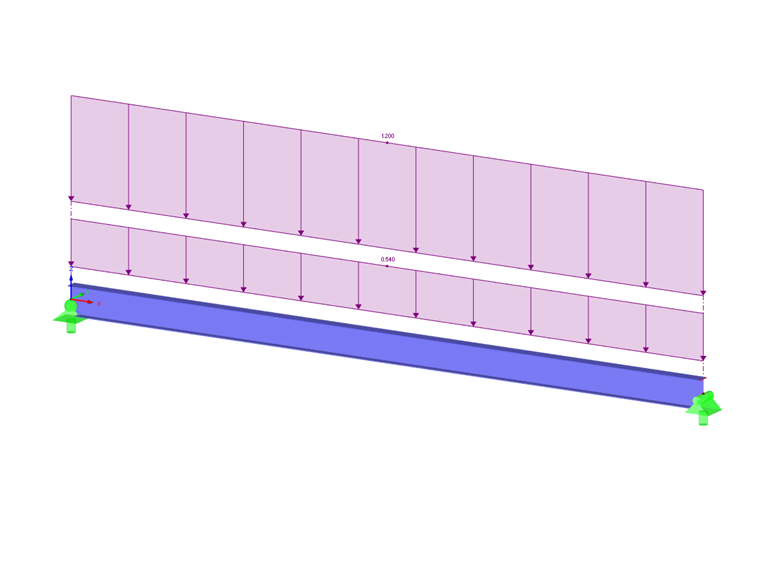
In the AISC 360-16 [1] standard, Chapter F, the modification Factor (Cb) is calculated based on the maximum moment at the midspan and quarter points along the beam using Eqn. F1-1. The unbraced length (Lr) and the limiting laterally unbraced length (Lp) must be calculated as well. For example, referring to F.1-2b taken from the AISC Verification problems [2], a W18X50 cross-section includes an applied uniform load. This, along with the loading criteria, can be viewed in Figure 2. The material, Steel A992, will be used for the beam along with lateral restraints at the ends and third points. Self-weight of the beam will not be considered. Verified with hand calculations below, RF-STEEL AISC can be used to calculate the nominal flexural moment (Mn). This value is then compared to the required flexural strength (Mr,y).
First, the required flexural strength is calculated.
Mu = (ω ⋅ L2) / 8
Mu = 266.00 kip ⋅ ft.
Now, the lateral-torsional buckling modification factor (Cb) must be calculated for the center segment of the beam utilizing Eqn. F1-1 [1].
| Cb | Lateral-torsional buckling modification factor for nonuniform moment diagrams |
| Mmax | Absolute value of maximum moment in the unbraced segment. |
| MA | Absolute value of moment at quarter point of the unbraced segment. |
| MB | Absolute value of moment at centerline of the unbraced segment. |
| MC | Absolute value of moment at three-quarter point of the unbraced segment. |
Cb = 1.01
The lateral-torsional buckling modification factor (Cb) must be calculated for the end-span beam utilizing Eqn. F1-1 [1].
Cb = 1.46
The higher required strength and lower Cb will govern. Now, the limiting laterally unbraced length (Lb) for the limit state of yielding can be calculated.
Limiting Laterally Unbraced Length
| Lb | Limiting laterally unbraced length for the limit state of yielding |
| ry | Radius of gyration about y-axis |
| E | Modulus of Elasticity |
| Fy | Yield Strength |
Lb = 69.9 in. = 5.83 ft.
Using Eqn. F2-6 [1] for doubly symmetric I-shaped member, the limiting unbraced length for the limit state of inelastic lateral-torsional buckling is equal to:
| E | Modulus of Elasticity |
| Fy | Yield Strength |
| J | Torsional constant |
| Sx | Elastic section modulus taken about the x-axis |
| ho | Distance between flange centroids |
Lr = 203 in.
Now, the flexural yielding limit state and the inelastic lateral-torsional buckling limit state must be compared to determine which is controlling. The lesser controls (Lp < Lb ≤ Lr) which is used in the nominal strength (Mn) calculation.
| Cb | Lateral-torsional buckling modification factor for nonuniform moment diagrams. |
| Mp | Plastic flexural strength. |
| Fy | Yield Strength |
| Sx | Elastic section modulus taken about the x-axis. |
| Lb | Distance between braces. |
| Lp | Limiting laterally unbraced length for the limit state of yielding. |
| Lr | Limiting laterally unbraced length for the limit state of inelastic lateral-torsional buckling. |
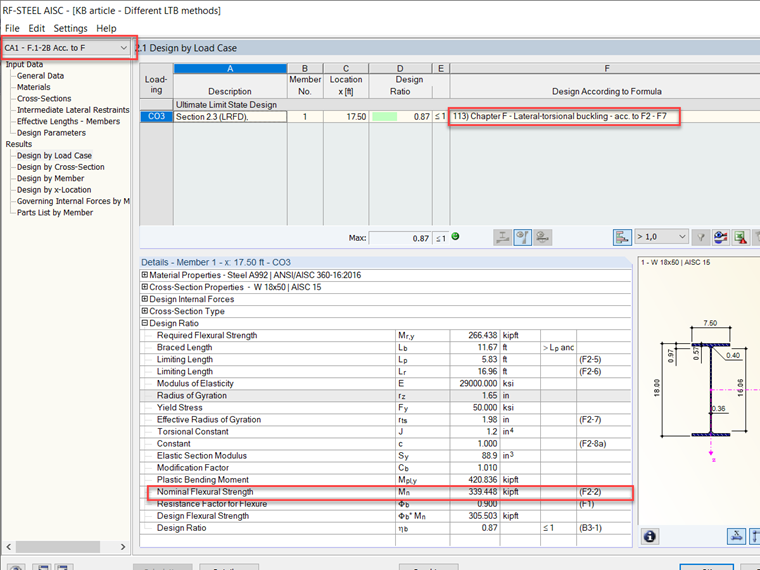
Mn = 339 kip-ft
Lastly, the resistance factor for flexural strength (φb) is multiplied by Mn to give the available flexural strength equal to 305 kip-ft.
Eigenvalue
The second analysis method to analyze LTB is according to an eigenvalue or Euler buckling analysis which predicts the theoretical buckling strength of an elastic structure, or in this case, a single beam member. When buckling takes place, eigenvalues are used to describe the values of loads. Then, eigenvectors are used to determine the shape of the eigenvalues that were calculated. When the resultant structure stiffness reaches zero, buckling takes place. The stress stiffness caused by a compressive load is removed from the elastic stiffness for this scenario. In most circumstances, the first few buckling modes are of most interest. [3]
Since an eigenvalue buckling analysis is theoretical and predicts the buckling strength of an elastic structure, this method is a more exact approach and differs from the AISC 360-16 [1] leading to a less conservative critical moment (Mcr) value.
Comparison
When comparing the results between the RFEM add-on module RF-STEEL AISC and the verification example F.1-2B [2] from the AISC 360-16 [1], the values are almost exact. The results are compared below in Figures 4 and 5 and the model can be downloaded below this article.
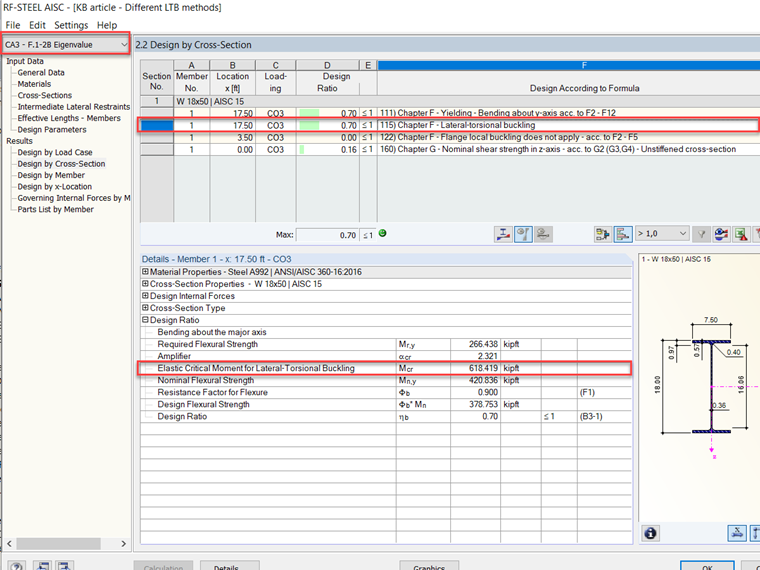
With RF-STEEL AISC, it is possible to run an eigenvalue analysis for calculating LTB. Example F.1-2B [2], referenced above, was modeled in RFEM and the results were calculated. You can see in Figure 6 the results from the eigenvalue analysis.
The same value calculated from the AISC Design Examples came out to be:
φbMn = 305 kip-ft
Mn according to Chapter F [1] in RF-STEEL AISC varies when compared to Mcr from an eigenvalue analysis. Fundamentally, the AISC 360-16 [1] standard takes a more conservative approach with analytical calculations compared to an eigenvalue analysis which is more theoretical and exact approach. It is expected for Mcr to be a larger value and you will see Mn is not equal to Mcr because if L.T.B is not controlling then Mn is equal to the controlling value between yielding or local buckling. Ultimately, it's up to the engineer's discretion which method or approach is suitable for their member design. Chapter F calculations are likely required but an eigenvalue analysis can provide a second look at LTB design from a theoretical standpoint for additional member capacity.
The steel AISC verification problems from Chapter F can be found on Dlubal Software's website where more details are shown comparing hand calculations to the results in RF-STEEL AISC. These are available in the link below with the model.
Author
Alex Bacon, EIT
Technical Support Engineer
Alex is responsible for customer training, technical support, and continued program development for the North American market.
Keywords
Steel Lateral torsional buckling AISC Eigenvalue
Reference
Links
Write Comment...
Write Comment...
Contact us
Do you have questions or need advice?
Contact our free e-mail, chat, or forum support or find various suggested solutions and useful tips on our FAQ page.
![[ZH] CP 001195 | Escalator trusses for commercial complexes in China](/-/media/Images/netgenium/thumbnails/2/9/6/9/0/2969057/2969057.png?la=en&mw=348&mlid=778F6A831FED4D2FA656FFF961A20361&hash=9EBB4DACB9DBE807C4A4A63A03C40211819DA585)
![[CS] CP 001194 | Renovation of an Existing Water Tower into an Office Building](/-/media/Images/netgenium/thumbnails/2/9/6/6/6/2966620/2966620.png?la=en&mw=348&mlid=2D4F0809D4D4457F82F841389157725E&hash=4F5308A0503F5C81B836C2A45F8DE998081E698C)
![[DE] CP 001193 | Hobro Arrest Prison Scaffolding, Denmark](/-/media/Images/netgenium/thumbnails/2/9/6/6/6/2966608/2966608.png?la=en&mw=348&mlid=009873CC759B413CAB8A477C624F3044&hash=9826E281910961C92AA70555B9AF5B125FAC9FB8)
New
Manual adjustment of the buckling curve according to EN 1993-1-1
The RF-/STEEL EC3 add-on module automatically transfers the buckling line to be used for the flexural buckling analysis for a cross-section from the cross-section properties. In particular for general cross -sections, but also for special cases, the assignment of the buckling line can be adjusted manually in the module input.
![Distribution of Forces and Moments in Column Base According to [1]](/-/media/Images/website/img/000001-010000/009601-009700/009638.png?la=en&mlid=7D34CEAAE7354583A29169095622B515&hash=D5A1CD829CEAC6F92DF0C68F3F0F37A7E0C0E89B)
![System and Loading According to [1]](/-/media/Images/website/img/000001-010000/009601-009700/009634.png?la=en&mlid=F0F0A23924B8424CA1C2905961DF676B&hash=6AC023A421BDDF6BFE2AC5D69132D2F81A0C365A)
SHAPE-THIN | Cold-Formed Sections
SHAPE-THIN determines the effective cross-sections according to EN 1993-1-3 and EN 1993-1-5 for cold-formed sections. You can optionally check the geometric conditions for the applicability of the standard specified in EN 1993‑1‑3, Section 5.2.
The effects of local plate buckling are considered according to the method of reduced widths and the possible buckling of stiffeners (instability) is considered for stiffened sections according to EN 1993-1-3, Section 5.5.
As an option, you can perform an iterative calculation to optimize the effective cross-section.
You can display the effective cross-sections graphically.
Read more about designing cold-formed sections with SHAPE-THIN and RF-/STEEL Cold-Formed Sections in this technical article: Design of a Thin-Walled, Cold-Formed C-Section According to EN 1993-1-3.
- Why do I get large differences for the design of a longitudinally stiffened buckling panel in comparison with the German and Austrian National Annex?
- How can I create a curved or arched section?
- How can I perform the stability analysis in RF‑/STEEL EC3 for a flat bar supported on edges, such as 100/5? Although the cross-section is rotated by 90° in RFEM/RSTAB, it is displayed as lying flat in RF‑/STEEL EC3.
- How are the signs for the release results of a line release and line hinges interpreted?
- How are hot-dip galvanized components considered for fire resistance in the RF‑/STEEL EC3 add-on module?
- How is the rotational stiffness of a buckling stiffener determined in PLATE‑BUCKLING?
- In RF-/STEEL EC3, is the "Elastic design (also for cross-section class 1 and 2)" option under "Details → Ultimate Limit State" considered for the stability analysis when activated?
- How can I get the member end forces to design the connections?
- I would like to calculate and design "temporary structures." What do I need for this?
- How can I create a drilled beam in RFEM?
Associated Products
Main Program
Structural engineering software for finite element analysis (FEA) of planar and spatial structural systems consisting of plates, walls, shells, members (beams), solids and contact elements
3,540.00 USD
Add-on Module
Design of steel members according to the American standard ANSI/AISC 360
1,480.00 USD
