Einführung
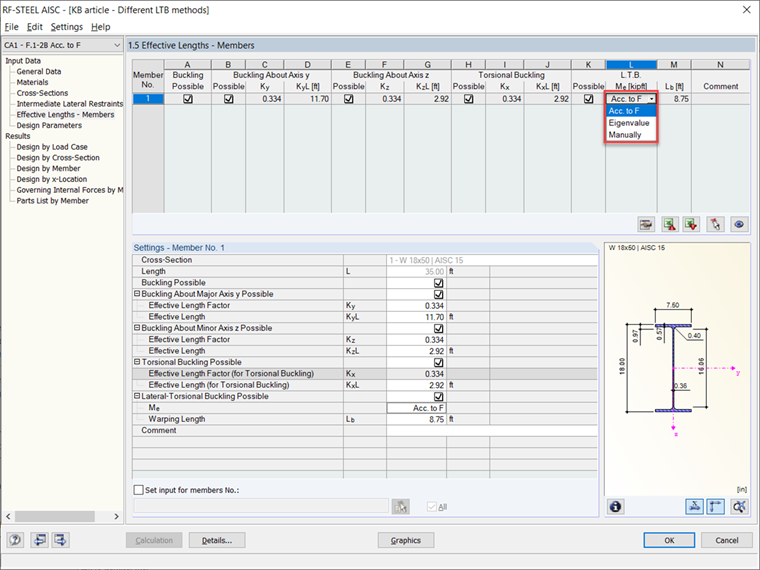
Bei der Konstruktion von Stahlträgern wird im Add-On RF-STAHL AISC standardmäßig das Biegedrillknicken (BGDK) berücksichtigt. Es stehen mehrere Methoden zur Stabilitätsanalyse zur Auswahl. Die erste Methode besteht darin, das BGDK gemäß dem Standard AISC 360-16, Kapitel F, zu berechnen. Bei der anderen Methode wird RFEM eine Eigenwertberechnung durchführen, um die maßgeblichen Stabilitätsbedingungen und das elastische kritische Moment (Mcr) zu berechnen. Diese Methoden werden alle in Tabelle 1.5 Knicklängen – Stäbe angezeigt und können im Dropdown-Menü geändert werden.
Kapitel F
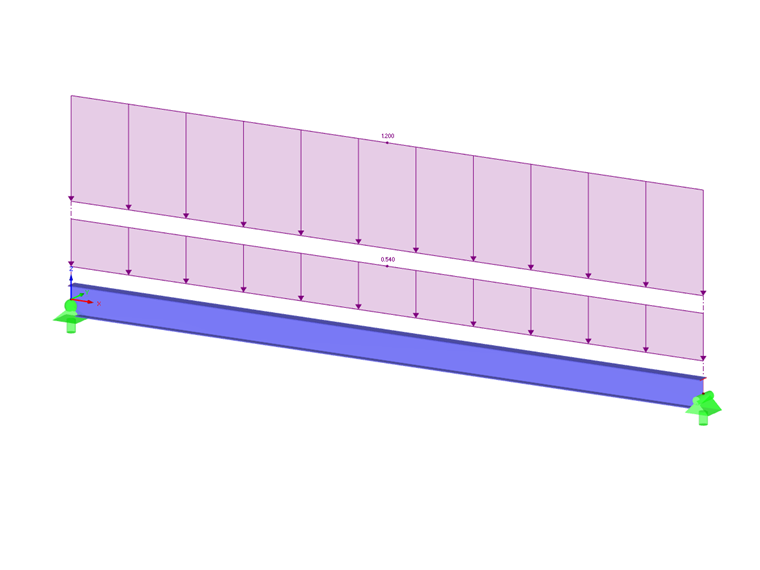
Im Standard AISC 360-16, Kapitel F, wird der Modifikationsbeiwert (C_b) auf der Grundlage des maximalen Moments an den Mittelspann- und Viertelpunkten entlang des Trägers unter Verwendung der folgenden Gleichung berechnet: Die unverspannte Länge (Lr) und die limitierende seitlich unverspannte Länge (Lp) müssen ebenfalls berechnet werden. Ein W18X50-Querschnitt beispielsweise umfasst gemäß F.1-2b aus den AISC-Verifizierungsproblemen [2] eine aufgebrachte gleichmäßige Last. Dies kann zusammen mit den Belastungskriterien in Image 2 angezeigt werden. Für den Träger wird das Material Stahl A992 zusammen mit seitlichen Stützungen an den Enden sowie dritten Punkten verwendet. Das Eigengewicht des Trägers wird dabei nicht berücksichtigt. RF-STAHL AISC wurde unten mit Handberechnungen verifiziert und kann zur Berechnung des nominalen Biegemoments (Mn) verwendet werden. Dieser Wert wird anschließend mit der erforderlichen Biegefestigkeit (Mr,y) verglichen.
Zunächst wird die erforderliche Biegefestigkeit berechnet.
Mu = (ω ⋅ L2) / 8
Mu = 266.00 kip ⋅ ft.
Nun muss der Modifikationsbeiwert des Biegedrillknickens (Cb) für das Mittelsegment des Trägers unter Verwendung der Gleichung F1-1 [1] berechnet werden.
|
Cb |
Lateral-torsional buckling modification factor for non-uniform moment diagrams |
|
Mmax |
Absolute value of the maximum moment in the unbraced segment |
|
MA |
Absolute value of the moment at the quarter point of the unbraced segment |
|
MB |
Absolute value of the moment at the centerline of the unbraced segment |
|
MC |
Absolute value of the moment at the three-quarter point of the unbraced segment |
Cb = 1,01
Der Modifikationsbeiwert für das Biegedrillknicken (Cb) muss für den Endabschnitt des Trägers mittels der Gleichung F1-1 [1] berechnet werden.
Cb = 1,46
Die höhere erforderliche Festigkeit und das niedrigere Cb werden maßgeblich sein. Anschließend kann die limitierende seitlich unverspannte Länge (Lb) für den Grenzzustand der Plastizierung berechnet werden.
|
Lb |
Limiting laterally unbraced length for the limit state of yielding |
|
ry |
Radius of gyration about the y-axis |
|
E |
Modulus of elasticity |
|
Fy |
Yield strength |
Lb = 69,9 Zoll = 5,83 ft.
Bei einem doppelsymmetrischen I-förmigen Stab ist die begrenzende nicht abgestützte Länge für den Grenzzustand des unelastischen Biegedrillknickens unter Verwendung der Gleichung F2-6 [1] gleich:
|
E |
Modulus of elasticity |
|
Fy |
Yield strength |
|
J |
Torsional constant |
|
Sx |
Elastic section modulus taken about the x-axis |
|
ho |
Distance between the flange centroids |
Lr = 203 Zoll
Nun müssen der Grenzzustand der Biegefestigkeit und der Grenzzustand des unelastischen Biegedrillknickens verglichen werden, um zu bestimmen, welcher maßgebend ist. Der kleinere Wert bestimmt (Lp < Lb ≤ Lr), der für die Berechnung der nominellen Festigkeit (Mn) verwendet wird.
|
Cb |
Lateral-torsional buckling modification factor for non-uniform moment diagrams |
|
Mp |
Plastic flexural strength |
|
Fy |
Yield strength |
|
Sx |
Elastic section modulus taken about the x-axis |
|
Lb |
Distance between braces |
|
Lp |
Limiting laterally unbraced length for the limit state of yielding |
|
Lr |
Limiting laterally unbraced length for the limit state of inelastic lateral-torsional buckling |
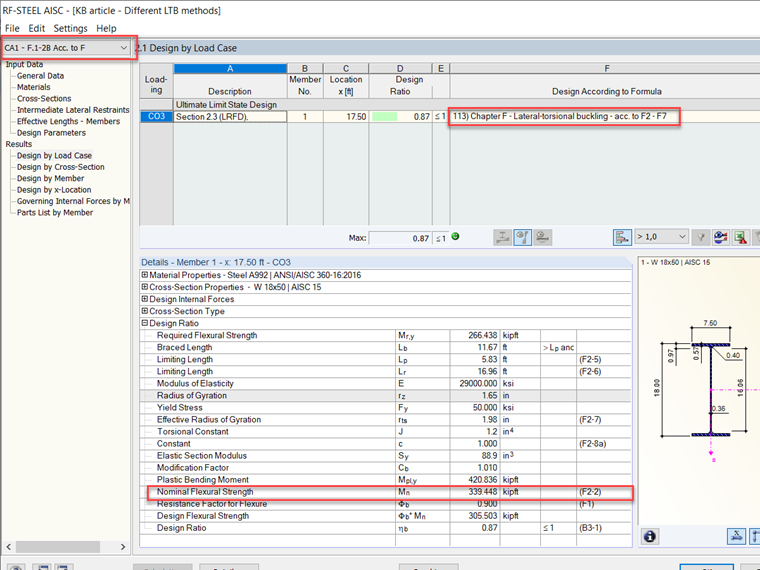
Mn = 339 kip-ft
Anschließend wird der Widerstandsbeiwert für die Biegefestigkeit (φb) mit Mn multipliziert, um die verfügbare Biegefestigkeit von 305 kip-ft zu erhalten.
Eigenwert
Die andere Methode zur Berechnung von BGDK basiert auf einer Eigenwert- oder Euler-Knickanalyse. Dabei wird die theoretische Knickfestigkeit einer elastischen Struktur – in diesem Fall eines einzelnen Balkenstabs – ermittelt. Beim Knicken werden Eigenwerte verwendet, um die Lasten zu beschreiben. Anschließend werden Eigenvektoren verwendet, um die Form der berechneten Eigenwerte zu bestimmen. Wenn die resultierende Struktursteifigkeit den Wert Null erreicht, kommt es zum Knicken. Die durch eine Druckbelastung verursachte Spannungssteifigkeit wird in diesem Szenario von der elastischen Steifigkeit getrennt. In den meisten Fällen sind die ersten Knickmodi am interessantesten. [3]
Da der Eigenwert-Knicknachweis eine theoretische Methode zur Bestimmung der Knickfestigkeit elastischer Strukturen ist, ist dieser Ansatz genauer als die AISC-360-16-Methode [1], was zu einem weniger konservativen kritischen Momentwert (Mcr) führt.
Vergleich
Beim Vergleich der Ergebnisse des Add-Ons RF-STAHL AISC in RFEM mit dem Verifizierungsbeispiel F.1-2B [2] aus dem AISC 360-16 [1] sind die Werte nahezu exakt. Die Ergebnisse werden in den unten stehenden Bildern 4 und 5 gegenübergestellt. Das Modell kann unter diesem Artikel heruntergeladen werden.
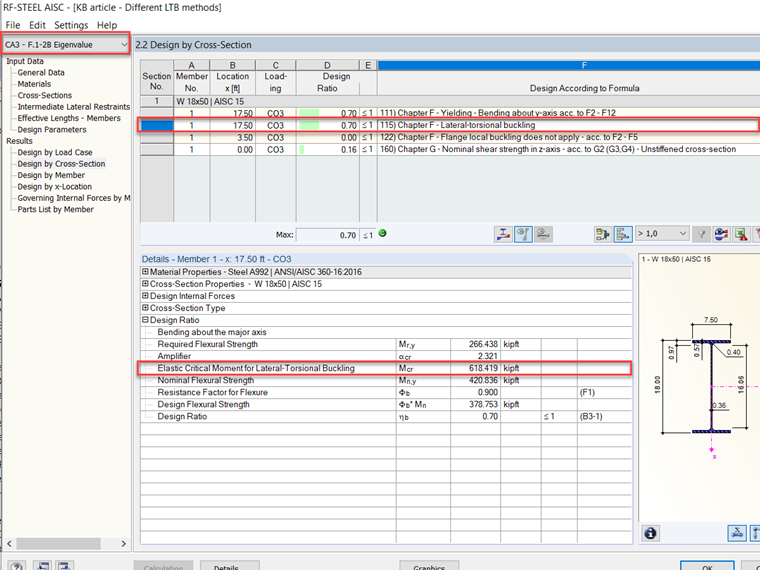
Mit dem Add-On RF-STEEL AISC ist es möglich, eine Eigenwertanalyse zur Berechnung von BGDK durchzuführen. Beispiel F.1-2B [2], auf das oben verwiesen wurde, wurde in RFEM modelliert und die Ergebnisse berechnet. Die Ergebnisse der Eigenwertanalyse sind in Bild 6 zu sehen.
Derselbe Wert, der aus den AISC-Bemessungsbeispielen berechnet wurde, ergab Folgendes:
φbMn = 305 kip-ft
Mn gemäß Kapitel F [#Refer [1]] in RF-STAHL AISC variiert im Vergleich zu Mcr aus einer Eigenwertanalyse. Grundsätzlich verfolgt der Standard AISC 360-16 einen konservativeren Ansatz mit analytischen Berechnungen als die eher theoretische und exakte Eigenwertanalyse. Es wird erwartet, dass Mcr ein größerer Wert ist. Dabei kann festgestellt werden, dass Mn nicht gleich Mcr ist, denn wenn BGDK nicht kontrolliert wird, dann ist Mn gleich dem Kontrollwert zwischen Fließen oder der lokalen Beulgefahr. Letztendlich entscheidet der Ingenieur, welche Methode oder welcher Ansatz für die Konstruktion am besten geeignet ist. Zwar sind Berechnungen gemäß Kapitel F wahrscheinlich erforderlich, doch kann eine Eigenwertberechnung aus theoretischer Sicht eine andere Perspektive auf die BGDK-Bemessung hinsichtlich zusätzlicher Stabkapazität bieten.
Die AISC-Verifikationsprobleme aus Kapitel F sind auf der Webseite von Dlubal Software zu finden. Dort werden weitere Details gezeigt und die Handberechnungen mit den Ergebnissen in RF-STAHL AISC verglichen. Diese stehen unter dem unten stehenden Link mit dem Modell zur Verfügung.