Introduzione
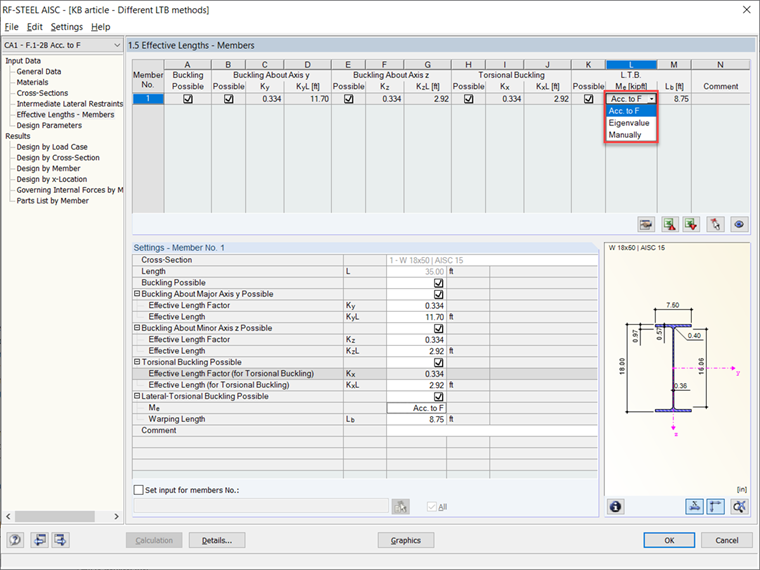
Nel modulo aggiuntivo RF-STEEL AISC, il fenomeno del carico critico per instabilità flessionale-torsionale (LTB) è considerato per impostazione predefinita quando si progettano travi in acciaio. Ci sono un paio di metodi di analisi della stabilità tra cui scegliere. Il primo metodo è quello di calcolare il LTB secondo lo standard AISC 360-16 [1] capitolo F. Il secondo metodo è far eseguire a RFEM un'analisi degli autovalori per calcolare le condizioni di stabilità governanti e il momento critico elastico (Mcr). Questi metodi si trovano tutti nella Tabella 1.5 Lunghezze Effettive - Membri e possono essere cambiati nel menu a tendina.
Capitolo F
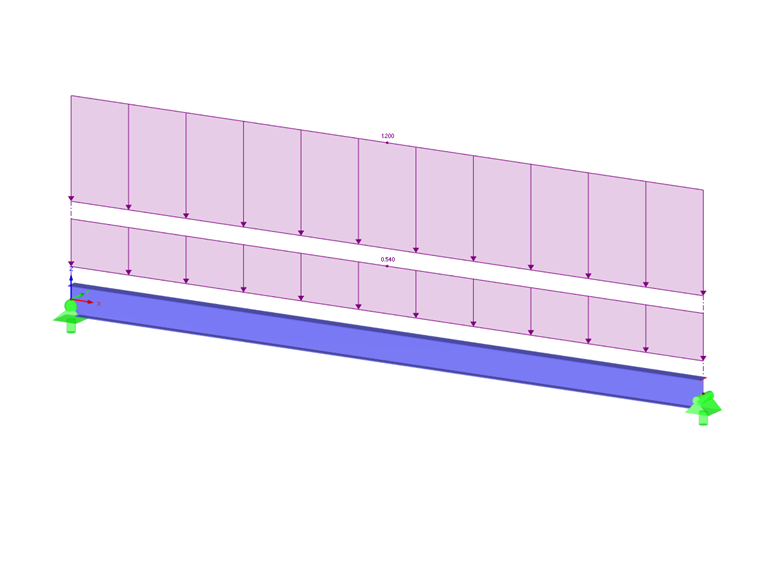
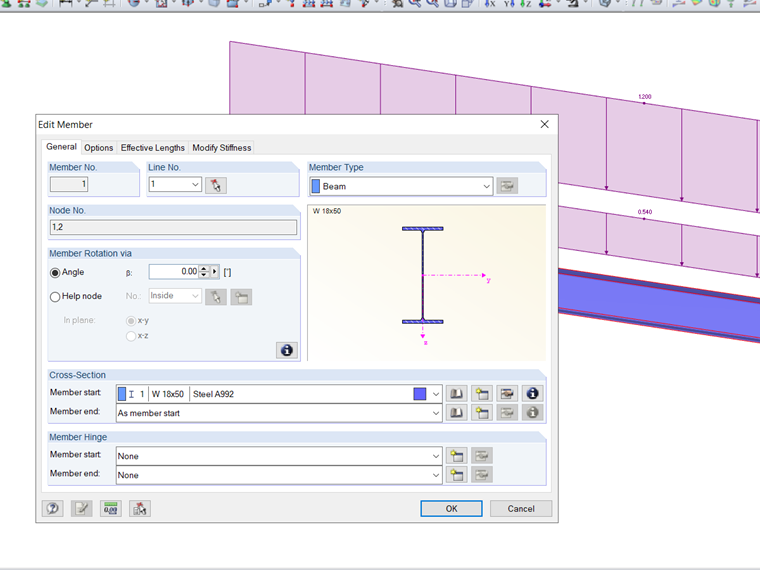
Nello standard AISC 360-16 [1] capitolo F, il fattore di modifica (Cb) viene calcolato sulla base del momento massimo nel punto medio e nei punti di quarto della trave utilizzando l'Eqn. F1-1. La lunghezza non bloccata (Lr) e la lunghezza limite non bloccata lateralmente (Lp) devono essere calcolate anch'esse. Ad esempio, riferendosi a F.1-2b tratto dai problemi di verifica AISC [2], una sezione W18X50 include un carico uniforme applicato. Questo, insieme ai criteri di carico, può essere visualizzato nell'immagine 2. Il materiale, Acciaio A992, sarà utilizzato per la trave insieme ai vincoli laterali alle estremità e ai terzi punti. Il peso proprio della trave non sarà considerato. Verificato con i calcoli manuali di seguito, RF-STEEL AISC può essere utilizzato per calcolare il momento nominale flessionale (Mn). Questo valore viene poi confrontato con la resistenza flessionale richiesta (Mr,y).
Innanzitutto, si calcola la resistenza flessionale richiesta.
Mu = (ω ⋅ L2) / 8 Mu = 266.00 kip ⋅ ft.
Ora, il fattore di modifica per instabilità flessionale-torsionale (Cb) deve essere calcolato per il segmento centrale della trave utilizzando l'Eqn. F1-1 [1].
|
Cb |
Lateral-torsional buckling modification factor for non-uniform moment diagrams |
|
Mmax |
Absolute value of the maximum moment in the unbraced segment |
|
MA |
Absolute value of the moment at the quarter point of the unbraced segment |
|
MB |
Absolute value of the moment at the centerline of the unbraced segment |
|
MC |
Absolute value of the moment at the three-quarter point of the unbraced segment |
Cb = 1,01
Il fattore di modifica per instabilità flessionale-torsionale (Cb) deve essere calcolato per la trave di fine campata utilizzando l'Eqn. F1-1 [1].
Cb = 1,46
La resistenza richiesta più alta e il Cb inferiore prevarranno. Ora, la lunghezza non bloccata lateralmente limite (Lb) per lo stato limite di snervamento può essere calcolata.
|
Lb |
Limiting laterally unbraced length for the limit state of yielding |
|
ry |
Radius of gyration about the y-axis |
|
E |
Modulus of elasticity |
|
Fy |
Yield strength |
Lb = 69,9 in. = 5,83 ft.
Utilizzando l'Eqn. F2-6 [1] per un elemento a forma di I simmetrico su entrambi gli assi, la lunghezza non bloccata limite per lo stato limite di instabilità flessionale-torsionale inelastica è pari a:
|
E |
Modulus of elasticity |
|
Fy |
Yield strength |
|
J |
Torsional constant |
|
Sx |
Elastic section modulus taken about the x-axis |
|
ho |
Distance between the flange centroids |
Lr = 203 inches
Ora, lo stato limite di snervamento flessionale e lo stato limite di instabilità flessionale-torsionale inelastica devono essere confrontati per determinare quale governa. Il minore governa (Lp < Lb ≤ Lr) che viene utilizzato nel calcolo della resistenza nominale (Mn).
|
Cb |
Lateral-torsional buckling modification factor for non-uniform moment diagrams |
|
Mp |
Plastic flexural strength |
|
Fy |
Yield strength |
|
Sx |
Elastic section modulus taken about the x-axis |
|
Lb |
Distance between braces |
|
Lp |
Limiting laterally unbraced length for the limit state of yielding |
|
Lr |
Limiting laterally unbraced length for the limit state of inelastic lateral-torsional buckling |
Mn = 339 kip-ft
Infine, il fattore di resistenza per la resistenza flessionale (φb) viene moltiplicato per Mn per ottenere la resistenza flessionale disponibile pari a 305 kip-ft.
Autovalore
Il secondo metodo di analisi per analizzare il LTB è un'analisi degli autovalori o dell'instabilità di Eulero che prevede la resistenza all'instabilità teorica di una struttura elastica, o in questo caso, di un singolo elemento trave. Quando si verifica un'instabilità, si utilizzano gli autovalori per descrivere i valori dei carichi. Poi, si utilizzano gli autovettori per determinare la forma degli autovalori calcolati. Quando la rigidità risultante della struttura raggiunge lo zero, si verifica un'instabilità. La rigidità degli stress causata da un carico di compressione viene rimossa dalla rigidità elastica per questo scenario. Nella maggior parte delle circostanze, i primi pochi modi di instabilità sono di massimo interesse. [3]
Dal momento che un'analisi di instabilità degli autovalori è teorica e prevede la resistenza all'instabilità di una struttura elastica, questo metodo è un approccio più preciso e differisce dallo standard AISC 360-16 [1], portando a un valore di momento critico (Mcr) meno conservativo.
Confronto
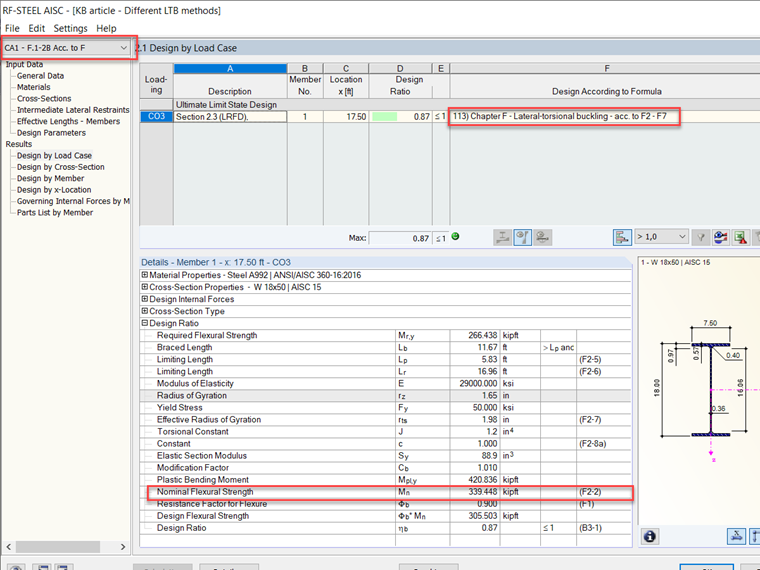
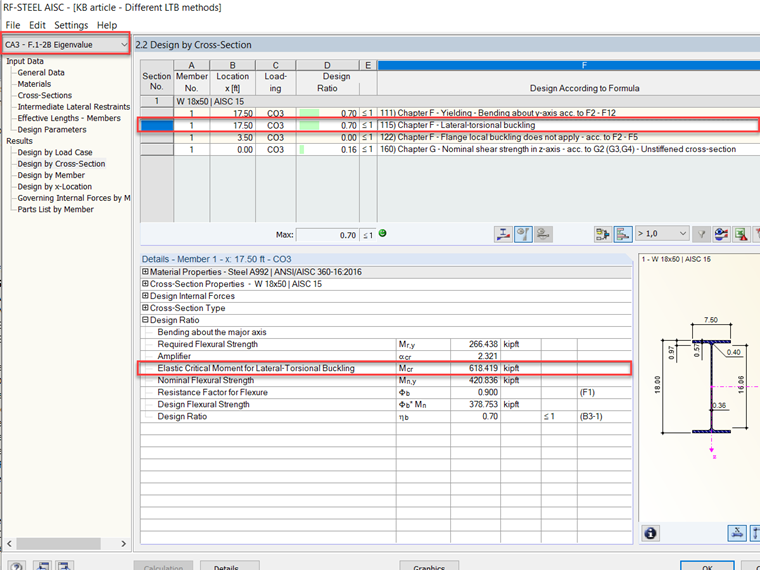
Confrontando i risultati tra il modulo aggiuntivo RFEM RF-STEEL AISC e l'esempio di verifica F.1-2B [2] dallo standard AISC 360-16 [1], i valori sono quasi esatti. I risultati sono confrontati di seguito nelle immagini 4 e 5, e il modello può essere scaricato sotto questo articolo.
Con RF-STEEL AISC, è possibile eseguire un'analisi degli autovalori per calcolare il LTB. L'esempio F.1-2B [2], citato sopra, è stato modellato in RFEM e i risultati sono stati calcolati. Puoi vedere i risultati dell'analisi degli autovalori nell'immagine 6.
Lo stesso valore calcolato dagli esempi di progettazione AISC è risultato: φbMn = 305 kip-ft
Mn secondo il capitolo F [1] in RF-STEEL AISC varia rispetto a Mcr da un'analisi degli autovalori. Fondamentalmente, lo standard AISC 360-16 [1] adotta un approccio più conservativo con i calcoli analitici rispetto a un'analisi degli autovalori, che è un approccio più teorico e preciso. Ci si aspetta che Mcr sia un valore maggiore, e vedrai che Mn non è uguale a Mcr perché se il LTB non controllo, allora Mn è uguale al valore di controllo tra snervamento o instabilità locale. In ultima analisi, è a discrezione dell'ingegnere quale metodo o approccio sia adatto per la progettazione del loro elemento. I calcoli del capitolo F sono probabilmente necessari, ma un'analisi degli autovalori può fornire una seconda occhiata alla progettazione LTB da un punto di vista teorico per una capacità dell'elemento aggiuntiva.
I problemi di verifica AISC dell'acciaio del capitolo F possono essere trovati nel sito web di Dlubal Software, dove sono mostrati più dettagli confrontando i calcoli manuali con i risultati in RF-STEEL AISC. Questi sono disponibili nel link sotto con il modello.