返回知识库

912x

001923

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

2025-06-04

使用梁柱厚度类型设计 CLT 板墙

在这篇文章中，将进行一种厚度类型为梁盘的木板墙的设计。

根据EC 5[1]，解释了在文章计算带有厚度类型梁盘的木板墙中介绍的木板墙的设计规则。材料和几何参数基于这篇文章；这里不再进行计算。

KB | 具有“厚度类型梁结构墙”厚度类型的木墙板的计算

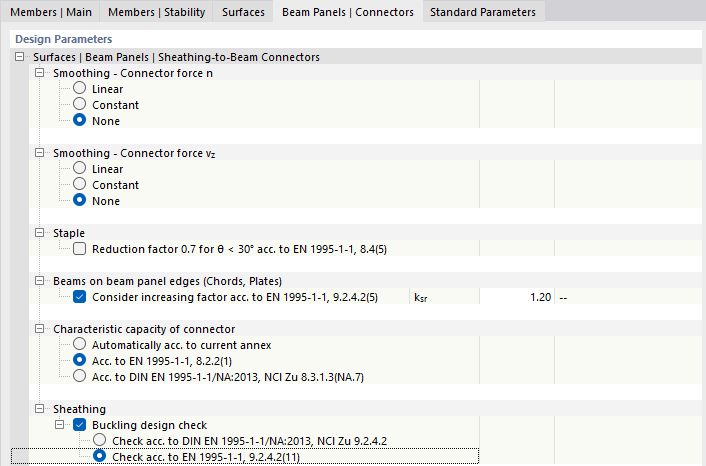
在“梁盘 | 连接件”选项卡中，为连接件（钉书钉1.5 x 50）的设计进行以下设置：

力不被平滑
无小于30°的减少（[1] 8.4(5)）
提高系数k_sr=1.2（[1] 9.2.4.2(5)）
根据Johansen的钉合同载能力（[1] 8.2.2(1)）
根据[1] 9.2.4.2(11)的简化屈曲校核

木框架墙的梁板的设计参数

木板墙单面覆板。

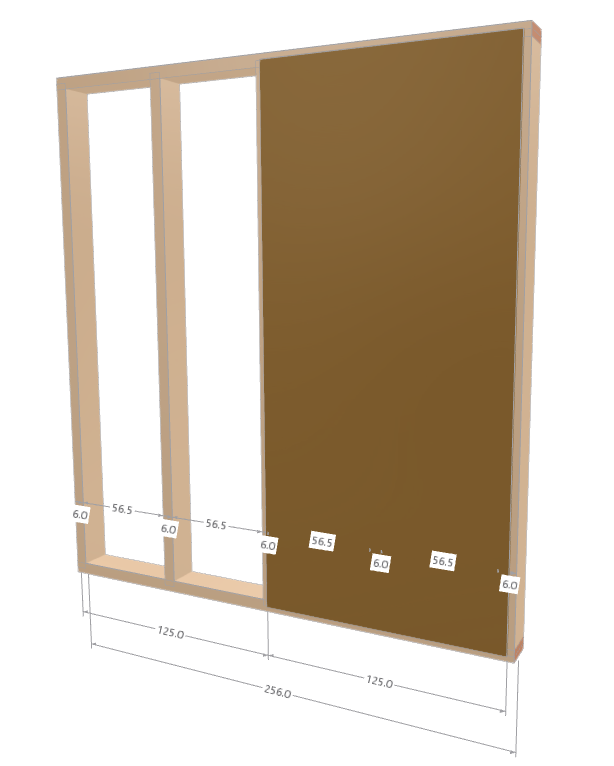
板材宽度设定为1.25 m，以考虑覆板的垂直接缝。这与前一篇文章中连续覆板有所不同。

RFEM 6 | 梁板上的覆层板缝

覆板的接缝适应边缘条的中线。长度为2.56 m时，会产生两个宽度为1.25 m的OSB板。板材左右两侧各有3 cm的自由边缘。以下图片显示了几何关系。

RFEM6 木墙板几何

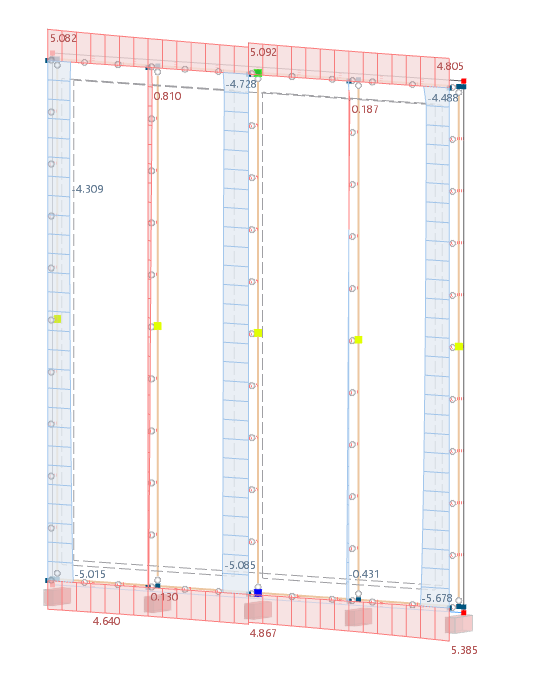
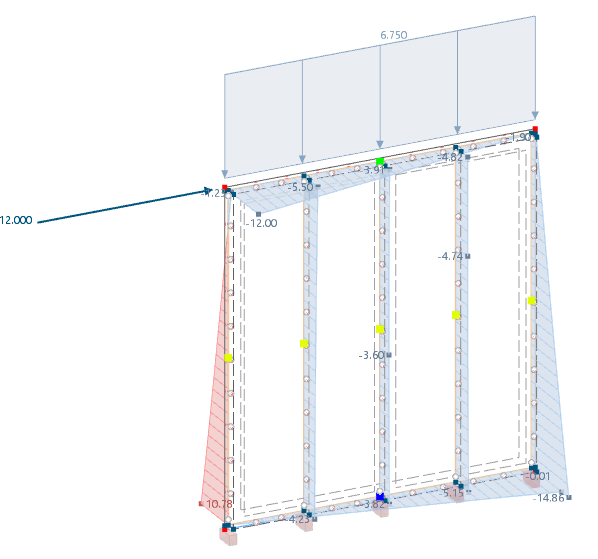
垂直荷载通过3D模型施加在上梁上。由于连续性效应，导致手工计算得出的法向力6.75 kN/m x 0.625 m = 4.22 kN不成立。

木墙板：RFEM 6 中的荷载分布

为说明这一点，将连续梁系统与上梁的单跨梁系统进行比较。对于荷载组合2 (1.35*LF1)，最大法向力为-4.7 kN，仅来自垂直荷载6.75 kN/m。图片中显示了考虑和未考虑连续效应的力。左侧显示了法向力和弯曲力，右侧则未考虑。图片左边显示了支撑力矩。

与之前的专业文章相比，这里定义了一个额外的线性支持，它表现出拉力。这样的建模更接近实际情况。

结合水平力，在载荷组合1 (1.35*LF1+1.5*LF2)中，后面立杆的轴力为-14 kN。

RFEM 6 木板墙中肋的轴向力

肋条被认为是侧向支撑以防扭曲和屈曲。需要进行绕强轴的屈曲校核 [1] 6.3.2。

立柱校核

木墙板梁板的稳定性分析

倾斜（不完善性）和风荷载将在空间计算的另一篇文章中讨论。

在覆板的校核中，需要研究三种失效模式。

连接件校核（剪切连接）
OSB/3板的剪切承载能力
覆板的屈曲

为了清晰呈现，以下两个方程的提供来自于DIN 1052 [2]。这些方程在编号123和124下。

f_{v, 0, d} = m i n \{\begin{cases} k_{v, 1} \cdot R_{d} / a_{v} \\ \overset{k_{v, 1} \cdot k_{v, 2} \cdot f_{v, d} \cdot t}{k_{v, 1} \cdot k_{v, 2} \cdot f_{v, d} \cdot 35 \cdot t^{2} / a_{r}} \end{cases}

DIN1052 长度相关抗剪强度

f_{v, 90, d} = m i n \{\begin{cases} R_{d} / a_{v} \\ \overset{k_{v, 2} \cdot f_{c, d} \cdot t}{k_{v, 2} \cdot f_{c, d} \cdot 20 \cdot t^{2} / a_{r}} \end{cases}

横向基于长度的强度 σύμφωνα με DIN1052

❶ 连接件校核

特征屈服力矩（[1] 8.29）

M_{y, Rk} = 150 \cdot d^{3} = 150 \cdot 1 . 5^{3} = 506.3 Nmm

屈服弯矩

拉伸强度假设为f_u,k = 900 N/mm²。

OSB板的孔压强度（[1] 8.22）

f_{h, k} = 65 d^{- 0, 7} t^{0, 1} = 65 \cdot 1, 5^{- 0, 7} \cdot 15^{0, 1} = 64, 16 N / m m^{2}

OSB 钉眼承载力

木材的孔压强度（[1] 8.15）

f_{h, k, 2} = 0, 082 \cdot ρ_{k, 2} \cdot {(d)}^{- 0, 3} = 0, 082 \cdot 350 k g / m ³ \cdot {(1, 5 m m)}^{- 0, 3} = 25, 4 N / m m^{2}

木材的承载力

孔压强度的比率（[1] 8.8）

β = \frac{f_{h, k, 2}}{f_{h, k, 1}} = \frac{25, 4}{64, 2} = 0, 4

孔壁承压强度

钉合同载能力（[1] 方程8.6 (a-f)）

根据欧洲规范 5，Johansen 的连接强度方程 8.6 a-f，范例 KB 001923

Johansen 的公式 8.6 a–f 用于计算夹具的承载力

通过程序输出显示钉书钉的承载能力。应使用最小值。在这种情况下，F_v,RK,min = 270.4 N

与之前的文章相似，一个钉书钉由两部分组成，因此该值可以翻倍。设计值为：

F_{v, R d} = \frac{2 \cdot F_{v, R k}}{γ_{M}} \cdot \sqrt{k_{m o d, 1} \cdot k_{m o d, 2}} = \frac{2 \cdot 270, 4 N}{1, 3} \cdot 1 = 416 N

设计强度

根据连接件的距离为50 mm得出的长度计算为：

f_{v, R d} = \frac{F_{v, R d}}{s} = \frac{416 N}{50 m m} = 8, 32 k N / m

连接件抗剪承载力

荷载由力n和v_z计算所得。以下图像显示了力。模型的第15号中线获得关键力。

连接件的受力

每个连接件的结果剪力为：

s_{v, d} = \sqrt{{(s_{v, o, d})}^{2} + {(s_{v, 9 o, d})}^{2}} = \sqrt{{(4, 71)}^{2} + {(3, 27)}^{2}} = 5, 73 k N / m

剪力连接器

从图像中可以清楚地看到，由于横向刚性的刚性耦合产生了局部明显的横向力峰值v_z。

为了避免这个问题，在接下来的梁盘设置中启用了“仅考虑纵向刚性的连接器刚性”选项。

仅考虑加劲件的纵向方向

因此，连接件仅产生纵向剪力，如以下图片所示。

连接件内力

立柱中的法向力变为14.86 kN。需要重新进行屈曲校核。由于负载率较低，可以忽略。

RFEM 6 木板墙肋中的正常力更大

仍然占主导地位的是两个覆板交接点15号内线。由于不存在横向力，消除了计算合力的需求。

校核1 – 连接件

η_{1} = \frac{s_{v, d}}{f_{v, R d}} = \frac{5, 09 k N / m}{8, 32 K N / m} = 0, 61

梁板设计

手工计算的剪力流结果相似。

s_{v, 0, d} = \frac{F}{L} = \frac{12 kN}{2.56 m} = 4.69 kN / m

切应力流

❷ 板的剪切承载能力文献[1] 9.21

单侧覆板k_da = 0.33 或 1 ([1] 方程NA.16)
f_v,d = 5.23 N/mm²
t = 15 mm

如果未选择校核1中选项“仅考虑连接器刚性在纵向”，则k_da = 1.0。

校核将如下所示。

η_{2} = \sqrt{{(\frac{s_{v, 0, d}}{k_{d a} \cdot f_{v, d} \cdot t})}^{2} + {(\frac{s_{v, 90, d}}{k_{d a} \cdot f_{c, d} \cdot t})}^{2}} = \sqrt{{(\frac{4, 71 k N / m}{1, 0 \cdot 5, 23 N / m m ² \cdot 15 m m})}^{2} + {(\frac{3, 27 k N / m}{1, 0 \cdot 9, 77 N / m m ² \cdot 15 m m})}^{2}} = 0, 06

面板剪切承载力

如果仅考虑纵向刚性，单侧覆板的系数为0.33，并将在下文中列出。

η_{2} = \sqrt{{(\frac{s_{v, 0, d}}{k_{d a} \cdot f_{v, d} \cdot t})}^{2} + {(\frac{s_{v, 90, d}}{k_{d a} \cdot f_{c, d} \cdot t})}^{2}} = \frac{5, 09 k N / m}{0, 33 \cdot 5, 23 N / m m ² \cdot 15 m m} = 0, 2

面板抗剪承载力（仅纵向）

由于仅考虑纵向的刚性，方程的后项为零。

❸ 板的剪切屈曲文献[1] 9.2.4.2

b_net = 565 mm (间隙肋条距离)
b_net/t = 565 mm / 15 mm = 37.7小于100

→ 简化的屈曲校核满足。

由于值大于35，进行更详细的德国NA校核。

OSB剪切强度f_v,k = 6.8 N/mm²
部分安全系数y_M = 1.3
调整系数k_mod = 1.0
根据NCI 9.2.4.2的系数k_da = 0.33或1
肋条距离a_r = 62.5 cm

如果在校核1中未选择选项“仅考虑连接器刚性在纵向”，则k_da = 1.0。

校核将如下所示。

η_{3} = \sqrt{{(\frac{s_{v, 0, d}}{k_{d a} \cdot f_{v, d} \cdot 35 \cdot \frac{t^{2}}{a_{r}}})}^{2} + {(\frac{s_{v, 90, d}}{k_{d a} \cdot f_{c, d} \cdot 20 \cdot \frac{t^{2}}{a_{r}}})}^{2}} = \sqrt{{(\frac{4, 71 k N / m}{1, 0 \cdot 5, 23 N / m m ² \cdot 35 \cdot \frac{{(15 m m)}^{2}}{625 m m}})}^{2} + {(\frac{3, 27 k N / m}{1, 0 \cdot 9, 77 \cdot 20 \cdot \frac{{(15 m m)}^{2}}{625 m m}})}^{2}} = 0, 09

蒙皮屈曲验算

如果仅考虑纵向刚性，单侧覆板的系数为0.33，并将在下文中列出。

η_{3} = \sqrt{{(\frac{s_{v, 0, d}}{k_{d a} \cdot f_{v, d} \cdot 35 \cdot \frac{t^{2}}{a_{r}}})}^{2} + {(\frac{s_{v, 90, d}}{k_{d a} \cdot f_{c, d} \cdot 20 \cdot \frac{t^{2}}{a_{r}}})}^{2}} = \frac{5, 09 k N / m}{0, 33 \cdot 5, 23 N / m m ² \cdot 35 \cdot \frac{{(15 m m)}^{2}}{625 m m}} = 0, 23

屈曲验算板件（仅限纵向）

由于仅考虑纵向刚性，也消除了该校核中的后置项。

提示

下载带有厚度类型梁盘的木板墙的模型文件。除了此处解释的示例外，文件中还包含结构，以便理解立柱的连续效应。

模型文件

174x

71x

木板墙的设计

作者

Kuhn 先生负责木结构产品的开发工作，并为客户提供技术支持。

链接

KB | 具有“厚度类型梁结构墙”厚度类型的木墙板的计算

参考

德国规范(2013)。国家附录 – 欧洲规范 5： Bemessung und Konstruktion von Holzbauten - Teil 1-1: Allgemeines - Allgemeine Regeln und Regeln für den Hochbau; DIN EN 1995-1-1/NA:2013-08
DIN 1052:2008-12： Entwurf, Berechnung und Bemessung von Holztragwerken − Allgemeine Bemessungsregeln und Regeln für den Hochbau. Beuth Verlag GmbH, Berlin, 2008

;