912x

001923

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

2025-06-04

Design of Timber Panel Wall with Beam Panel Thickness Type

In this article, the design of a timber panel wall with the beam panel thickness type is performed.

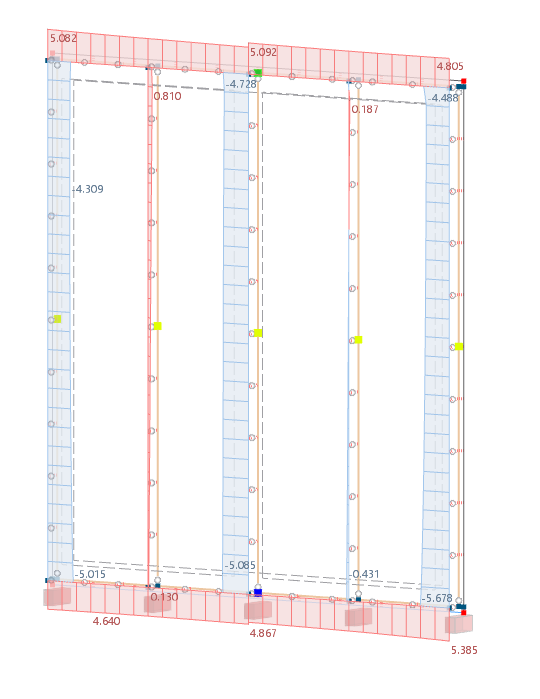
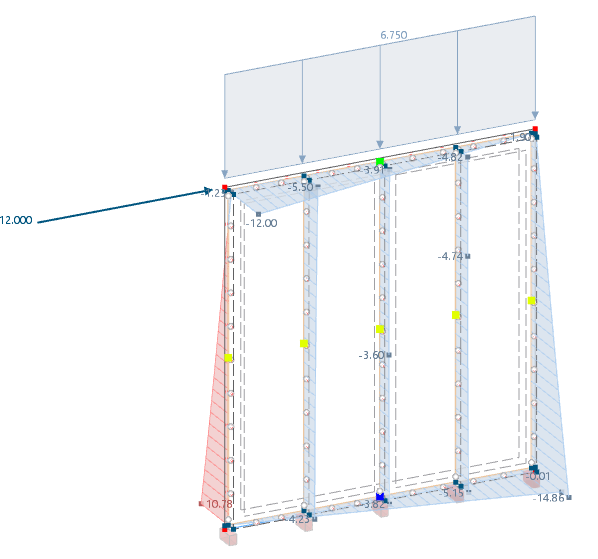
The design rules according to EC5 [1] are explained for the timber panel wall already presented in the article Design of Timber Panel Wall with Beam Panel Thickness Type. Material and geometry properties are based on this article; they are not determined here again.

KB | Design of Timber Panel Wall with Beam Panel Thickness Type

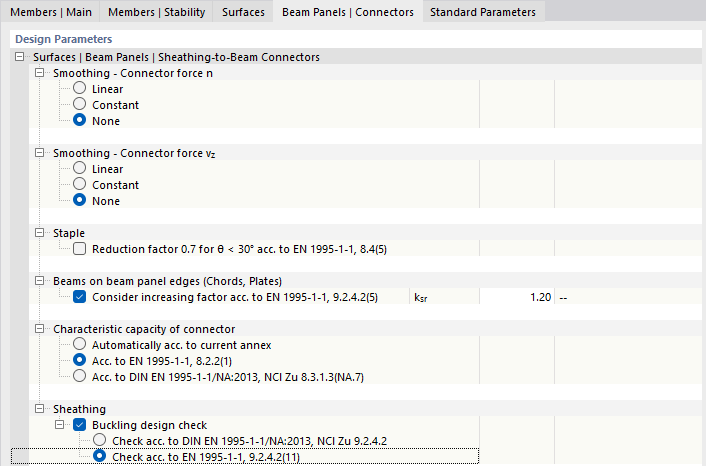
To design the fasteners (brackets 1.5 x 50), additional settings are made in the "Beam Panel | Connectors" tab:

Forces are not smoothed
No reduction smaller than 30° ([1], 8.4(5))
Increase factor k_sr=1.2 ([1] , 9.2.4.2(5))
Load-bearing capacity of the bracing according to Johansen ([1] , 8.2.2(1))
Buckling design simplified according to ([1] , 9.2.4.2(11))

Design parameters for a beam panel as a timber panel wall in accordance with Eurocode 5, Case KB 001923

Design Parameters of Beam Panel for Timber Panel Wall

The timber panel wall has sheathing on one side.
The plate width is applied with a length of 1.25 m. This takes into account the vertical joints in the sheathing. This is a difference from the continuous sheathing in the previous post.

RFEM 6 | Sheathing joints in a beam panel of a timber panel wall

RFEM 6 | Sheathing Joints in Beam Panel

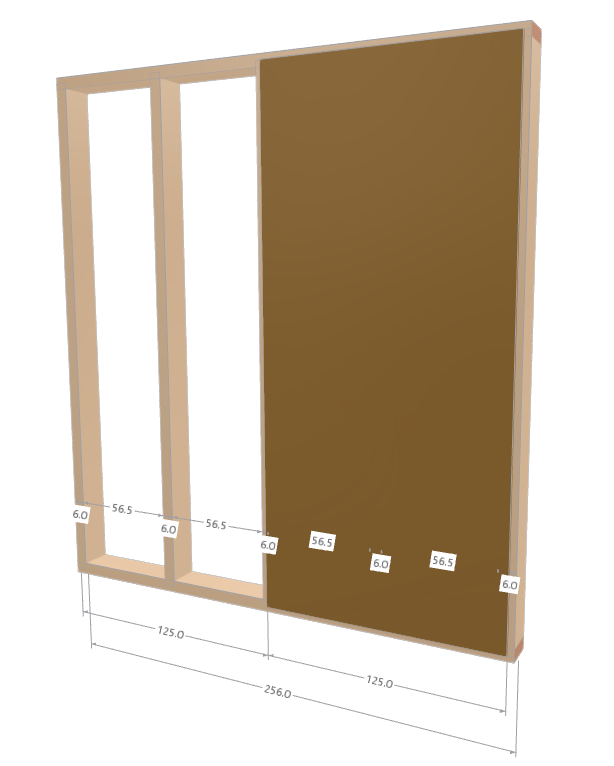
The joints in the sheeting are adjusted to the boundary member centerlines. With a length of 2.56 m, this results in two OSB boards, each with a width of 1.25 m. There is a 3 cm gap on the left and right sides of the board. The geometry is displayed in the following image.

Geometry of timber panel walls in RFEM 6

Geometry of Timber Panel Wall in RFEM 6

The vertical loads are introduced by the 3D model at the upper frame. The axial force of 6.75 kN/m × 0.625 m = 4.22 kN, which was calculated manually, does not result due to the continuous beam effect.

Timber panel wall model in RFEM 6 with axial forces without a continuous action and bending moments on ribs

Timber Panel Wall: Load Distribution in RFEM 6

For illustration purposes, the continuous beam system is compared with a single-span beam system of the upper frame. For Load Combination 2 (1.35*LC1), the maximum axial force of -4.72 kN results from a purely vertical load of 6.75 kN/m. The image shows axial forces with and without the continuity effects.

Compared to the previous technical article, an additional line support is defined here, which fails under tension. This makes the modeling more close to reality.

Together with the horizontal force, Load Combination 1 (1.35*LC1+1.5*LC2) results in a compressive force of -14 kN on the back support.

Simulation of the governing axial force distribution in the ribs of a timber panel wall in RFEM 6

Axial Force in Ribs of Timber Panel Wall in RFEM 6

Ribs are considered as laterally restrained against rotation and buckling. Buckling design is performed around the major axis according to [1], 6.3.2.

Design of Supports

Stability analysis of a beam panel as a timber panel wall according to Eurocode 5, Case KB 001923

Stability Analysis of Beam Panel for Timber Panel Wall

Inclinations (imperfections) and wind loads will be discussed in a future article on spatial calculation.

In the sheathing design, there are three failure modes to be analyzed.

Design of fasteners (shear connection)
Shear resistance of the OSB/3 board
Buckling of the sheathing

Based on the clear representation, the information from DIN 1052 [2] is listed in the following two equations. These equations can be found there under numbers 123 and 124.

f_{v, 0, d} = m i n \{\begin{cases} k_{v, 1} \cdot R_{d} / a_{v} \\ \overset{k_{v, 1} \cdot k_{v, 2} \cdot f_{v, d} \cdot t}{k_{v, 1} \cdot k_{v, 2} \cdot f_{v, d} \cdot 35 \cdot t^{2} / a_{r}} \end{cases}

Shear Strength Related to Length According to DIN 105

f_{v, 90, d} = m i n \{\begin{cases} R_{d} / a_{v} \\ \overset{k_{v, 2} \cdot f_{c, d} \cdot t}{k_{v, 2} \cdot f_{c, d} \cdot 20 \cdot t^{2} / a_{r}} \end{cases}

Design of Fasteners

Charcteristic yield moment ([1], 8.29)

M_{y, Rk} = 150 \cdot d^{3} = 150 \cdot 1 . 5^{3} = 506.3 Nmm

Characteristic Yield Moment

The tensile strength is assumed to be f_u,k = 900 N/mm².

M_{y, Rk} = 150 \cdot d^{3} = 150 \cdot 1 . 5^{3} = 506.3 Nmm

Characteristic Yield Moment

Hole bearing strength of the OSB board ([1], 8.22)

f_{h, k} = 65 d^{- 0, 7} t^{0, 1} = 65 \cdot 1, 5^{- 0, 7} \cdot 15^{0, 1} = 64, 16 N / m m^{2}

Hole Bearing Strength of OSB

Hole bearing strength of timber ([1], 8.15)

f_{h, k, 2} = 0, 082 \cdot ρ_{k, 2} \cdot {(d)}^{- 0, 3} = 0, 082 \cdot 350 k g / m ³ \cdot {(1, 5 m m)}^{- 0, 3} = 25, 4 N / m m^{2}

Hole Bearing Strength of Timber

Hole bearing strength ratio ([1], 8.8)

β = \frac{f_{h, k, 2}}{f_{h, k, 1}} = \frac{25, 4}{64, 2} = 0, 4

Hole Bearing Strength Ratio

Buckling resistance ([1], Equations 8.6 (a-f))

Load-bearing capacity of bracing Equations 8.6 a-f (Johansen) according to Eurocode 5, Case KB 001923

Resistance of Bracing – Equations 8.6 a-f (Johansen)

The load-bearing capacity of the brackets is displayed in the program printout. The minimum value has to be used. In this case, F_v,RK,min = 270.4 N

As in the previous post, a bracket consists of two pins, which is why the value can be doubled here. The resulting design value is:

F_{v, R d} = \frac{2 \cdot F_{v, R k}}{γ_{M}} \cdot \sqrt{k_{m o d, 1} \cdot k_{m o d, 2}} = \frac{2 \cdot 270, 4 N}{1, 3} \cdot 1 = 416 N

Design Resistence of Clamps

Related to the length with a fastener spacing of 50 mm.

f_{v, R d} = \frac{F_{v, R d}}{s} = \frac{416 N}{50 m m} = 8, 32 k N / m

Lengh-Related Load-Bearing Resistance of Connectors

The load is determined from the force n and v_z. The forces are displayed in the following image. Centerline 15 of the model obtains the governing forces.

Force in Fastener

Resulting shear force per connector.

s_{v, d} = \sqrt{{(s_{v, o, d})}^{2} + {(s_{v, 9 o, d})}^{2}} = \sqrt{{(4, 71)}^{2} + {(3, 27)}^{2}} = 5, 73 k N / m

Shear Force of Connector

Based on the image, it is clearly visible that, due to the stiffness in the transverse direction, very short but extreme transverse forces v_z arise.

To get around this problem, in the beam panel settings, "Connector stiffness in longitudinal direction only" is considered.

Considering the connector stiffness in the longitudinal direction only, Case B #001923

Considering Connector Stiffness in Longitudinal Direction Only

This results in only longitudinal shear forces in the connector, which are displayed in the following image.

Force in Fastener

The axial force in the support changes to 14.86 kN. It is necessary to perform the buckling design again. Based on the low load, this is not necessary.

Higher Axial Force in Ribs of Timber Panel Wall in RFEM 6

The inner line 15 at the point of contact between the two sheathing continues to be governing. The calculation of the resultant forces is not necessary, as there are no longer any transverse forces.

Design 1 – Fastener

η_{1} = \frac{s_{v, d}}{f_{v, R d}} = \frac{5, 09 k N / m}{8, 32 K N / m} = 0, 61

Design of Beam Panel Fastener

A manual comparative calculation of the shear flow results in similar values.

s_{v, 0, d} = \frac{F}{L} = \frac{12 kN}{2.56 m} = 4.69 kN / m

Shear Flow Loading

This value is calculated the same way in the result diagrams using the correct smoothing.

Display of a shear stress distribution in a timber wall panel using numerical parameters

Result Diagram of Shear Flow in Timber Panel Wall

Shear Resistance of Plate According to [1], 9.21

* Single-sided sheathing k_da = 0.33 or 1 ([1], Equation NA.16)
f_v,d = 5,23 N/mm²
t = 15 mm

If the “Consider connector stiffness in longitudinal direction only” option selected in Design 1 is not selected, the value for k_da is equal to 1.0.

The design then looks as follows.

η_{2} = \sqrt{{(\frac{s_{v, 0, d}}{k_{d a} \cdot f_{v, d} \cdot t})}^{2} + {(\frac{s_{v, 90, d}}{k_{d a} \cdot f_{c, d} \cdot t})}^{2}} = \sqrt{{(\frac{4, 71 k N / m}{1, 0 \cdot 5, 23 N / m m ² \cdot 15 m m})}^{2} + {(\frac{3, 27 k N / m}{1, 0 \cdot 9, 77 N / m m ² \cdot 15 m m})}^{2}} = 0, 06

Shear Resistance of Sheathing

If only the longitudinal stiffness is taken into account, the coefficient for single-sided sheathing is 0.33 and is listed below.

η_{2} = \sqrt{{(\frac{s_{v, 0, d}}{k_{d a} \cdot f_{v, d} \cdot t})}^{2} + {(\frac{s_{v, 90, d}}{k_{d a} \cdot f_{c, d} \cdot t})}^{2}} = \frac{5, 09 k N / m}{0, 33 \cdot 5, 23 N / m m ² \cdot 15 m m} = 0, 2

Shear Resistance of Sheathing (Longitudinal Direction Only)

The back term of the equation becomes zero, because the stiffness of the bracing is only applied in the longitudinal direction.

Shear Buckling of Plate According to [1], 9.2.4.2

b_net = 565 mm (clear distance of ribs)
b_net = 565 mm/15 mm = 37.7 less than 100

→ The simplified buckling design is fulfilled.

Since the value is greater than 35, a more precise design is carried out according to German NA.

Shear strength OSB f_v,k = 6.8 N/mm²
Partial safety factor y_M = 1.2
Modification factor k_mod = 1.0
Factor according to NCI 9.2.4.2 k_da = 0.33 or 1
Distance of ribs b_r = 62.5 cm

If the “Consider connector stiffness in longitudinal direction only” option selected in Design 1 is not selected, the value for k_da is equal to 1.0.

The design then looks as follows.

η_{3} = \sqrt{{(\frac{s_{v, 0, d}}{k_{d a} \cdot f_{v, d} \cdot 35 \cdot \frac{t^{2}}{a_{r}}})}^{2} + {(\frac{s_{v, 90, d}}{k_{d a} \cdot f_{c, d} \cdot 20 \cdot \frac{t^{2}}{a_{r}}})}^{2}} = \sqrt{{(\frac{4, 71 k N / m}{1, 0 \cdot 5, 23 N / m m ² \cdot 35 \cdot \frac{{(15 m m)}^{2}}{625 m m}})}^{2} + {(\frac{3, 27 k N / m}{1, 0 \cdot 9, 77 \cdot 20 \cdot \frac{{(15 m m)}^{2}}{625 m m}})}^{2}} = 0, 09

Buckling Analysis of Sheathing

If only the longitudinal stiffness is taken into account, the coefficient for single-sided sheathing is 0.33 and is listed below.

η_{3} = \sqrt{{(\frac{s_{v, 0, d}}{k_{d a} \cdot f_{v, d} \cdot 35 \cdot \frac{t^{2}}{a_{r}}})}^{2} + {(\frac{s_{v, 90, d}}{k_{d a} \cdot f_{c, d} \cdot 20 \cdot \frac{t^{2}}{a_{r}}})}^{2}} = \frac{5, 09 k N / m}{0, 33 \cdot 5, 23 N / m m ² \cdot 35 \cdot \frac{{(15 m m)}^{2}}{625 m m}} = 0, 23

Buckling Design of Sheathing (Longitudinal Direction Only)

Based on the fact that only the longitudinal stiffness is taken into account, the rear term is also omitted in this design.

Tip

Download the model file for the timber panel wall with the Beam Panel thickness type. In addition to the example explained here, the file also contains the structure for understanding the transfer effect on the supports.

Model File

174x

71x

Design of Timber Panel Wall

Author

Mr. Kuhn is responsible for developing products for timber structures, and provides technical support for our customers.

Links

KB | Design of Timber Panel Wall with Beam Panel Thickness Type

References

DIN. (2013). National Annex – Eurocode 5: Design of Timber Structures – Part 1-1: General – Common Rules and Rules for Buildings, DIN EN 1995-1-1/NA:2013-08. Berlin: Beuth Verlag GmbH.
DIN 1052:2008-12: Entwurf, Berechnung und Bemessung von Holztragwerken − Allgemeine Bemessungsregeln und Regeln für den Hochbau. Beuth Verlag GmbH, Berlin, 2008

;