ASCE 7-22 e Efeitos P-Delta
Norma ASCE 7-22 {%>[1], que declara que P-delta não precisa ser considerado quando o coeficiente de estabilidade (θ) determinado pela equação abaixo é igual ou inferior a 0,10.
| Px | Total vertical design load at and above level x per Sect. 12.8.6.1 (all load factors equal to or less than 1.0) |
| Vx/Δse | Rigidez de piso no nívelx, calculada como corte sísmico de cálculo, Vx , dividido pelo correspondente deslocamento elástico do piso, Δe |
| hsx | Altura do piso abaixo do piso x |
A norma continua a afirmar que θ não deve exceder o menor de θmax, dado pela equação abaixo, porque a estrutura é potencialmente insegura e deve ser redimensionada.
| Cd | Fator de amplificação da flecha na Tabela 12.2-1 |
| β | Relação entre exigências de corte e capacidade de corte de cálculo para o piso entre os pisos x e x-1 (considerado conservadoramente como 1,0, mas não inferior a 1,25/Ω0 ) |
Quando 0,10 < θ ≤ θmáx, é permitido para os deslocamentos e as forças da barra devem ser multiplicadas por um fator de 1,0/(1-θ). Em alternativa, os efeitos P-delta podem ser incluídos numa análise automatizada, onde as limitações θmáx ainda são aplicáveis.
Efeitos de NBC 2020 e de P-Delta
Enviado 4.1.8.3.8.c da NBC 2020 {%>x ) no nível x deve ser calculado com a seguinte equação abaixo.
| #formula@001475# | Parte do peso próprio mais carga variável no nível x |
| #formula@001476# | Soma das forças sísmicas laterais de cálculo atuantes ao nível x ou acima |
| Ro | Coeficiente de alteração da força relacionado com a sobrerresistência |
| Δmx | Deflexão não-elástica entre os pisos |
| hs | Altura entre os pisos |
Quando θx é menor que 0,10, então os efeitos P-delta podem ser ignorados. Quando θx é maior que 0,40, a estrutura deve ser redimensionada, pois é considerada insegura durante sismos extremos. Para 0,10 ≤ θx ≤ 0,40, as forças e momentos induzidos por sismos podem ser multiplicados por um fator de amplificação de (1 + θx ) para considerar P-delta. Este fator de amplificação não necessita de ser aplicado aos deslocamentos.
Consideração aproximada dos efeitos P-Delta com fatores de amplificação
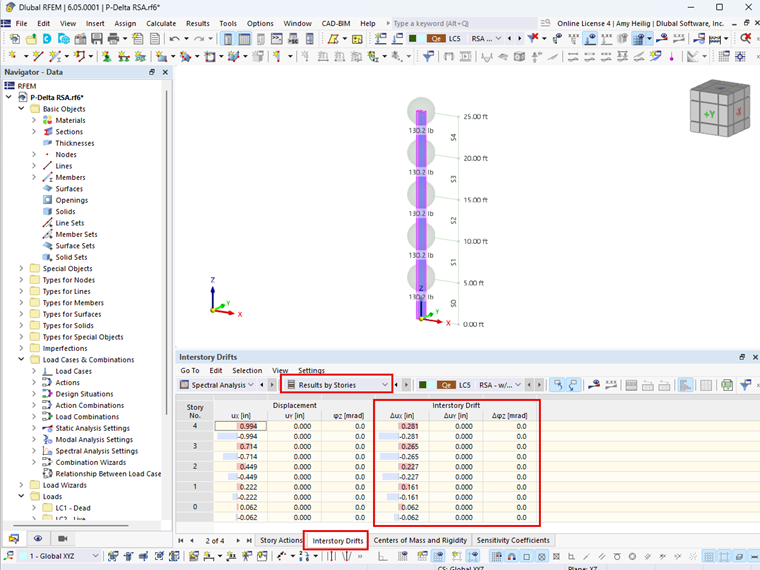
O valor do fator de estabilidade deve ser calculado nas duas direções horizontais ortogonais para determinar se P-delta é um problema. O deslocamento do piso Δ, necessário para calcular o coeficiente de estabilidade na ASCE 7-22 e na NBC 2020, é agora fornecido automaticamente no RFEM 6 com o módulo Dimensionamento da construção. Cada nível de piso incluirá o deslocamento do piso relevante na saída de resultados da tabela como apresentado na Figura 01.
Se uma ou ambas as direções requerem que os efeitos de segunda ordem sejam considerados dentro dos intervalos dados, o fator 1.0/(1-θ) da ASCE 7-22 ou (1+θx ) da NBC 2020 pode ser facilmente utilizado em RFEM 6 e módulo Análise de espectro de resposta. Todas as forças e/ou deflexões resultantes são aumentadas pelo valor definido.
Consideração mais precisa dos efeitos P-Delta com a matriz de rigidez geométrica
Embora os efeitos secundários podem ser estimados com os fatores de amplificação acima, esta é uma abordagem mais conservadora. Para cenários onde ocorrem grandes desvios de andares ou os efeitos P-delta precisam de ser calculados com uma abordagem mais exata, a influência das forças axiais pode ser ativada no módulo Análise de espectro de resposta.
Ao realizar uma análise dinâmica, os cálculos iterativos não lineares típicos para os efeitos da análise de segunda ordem não são mais aplicáveis ao considerar uma análise estática. O problema deve ser linearizado ativando a matriz de rigidez geométrica durante o cálculo. Com esta abordagem, assume-se que as cargas verticais não se alteram devido aos efeitos horizontais e que as deformações são pequenas em comparação com as dimensões globais da estrutura {%>
O conceito por trás da matriz de rigidez geométrica é o efeito de reforço de tensões. As forças axiais de tração levarão a um aumento da resistência à flexão de uma barra, enquanto que as forças axiais de compressão levarão a uma redução da resistência à flexão. Isto pode ser facilmente transmitido com o exemplo de um cabo ou um tirante delgado. Quando a barra experimenta uma força de tração, a resistência à flexão é significativamente maior do que quando a barra está sujeita a uma força de compressão. Quando sujeita a compressão, a barra tem muito pouca ou nenhuma rigidez à flexão para suportar uma carga lateral aplicada.
A matriz de rigidez geométrica Kg pode ser derivada das condições de equilíbrio estático.
Por simplificação, apenas os graus de liberdade dos deslocamentos horizontais são apresentados. A derivação apresentada é baseada na abordagem do momento de desvio devido à aplicação do deslocamento linear. Esta é uma simplificação para o elemento de flexão e uma suposição exata para o elemento de treliça. Tenha em atenção que a matriz depende apenas do comprimento do elemento e da força axial.
Pode ser obtida uma determinação mais precisa da matriz de rigidez geométrica para vigas de flexão através da abordagem do deslocamento cúbico ou da solução analítica da equação diferencial da linha de flexão. Mais informação sobre a teoria e as derivações é fornecidas por Werkle {%>
A matriz de rigidez geométrica "Kg" é adicionada à matriz de rigidez "K" e assim é obtida a matriz de rigidez modificada "Kmod":
Kmod = K + Kg
No caso de forças axiais de compressão, isso leva a uma redução na rigidez.
Exemplo de modificação da rigidez geométrica P-Delta no RFEM 6
A aplicação da redução de rigidez utilizando a matriz de rigidez geométrica para considerar os efeitos da teoria de segunda ordem (P-Delta) numa análise de espectro de resposta é realizada com uma estrutura em consola simples no RFEM 6. A barra é uma secção W 12x26 e material A992 com Iy = 204 in4 e E = 29000 ksi. Cada um dos 5 pisos tem 1,5 m, para uma altura total de 7,5 m.
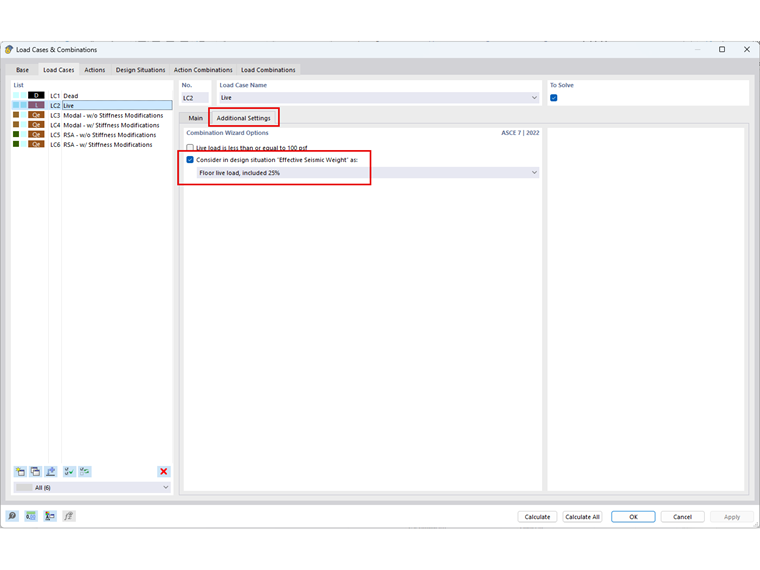
Não sendo considerado o peso próprio, é aplicada uma carga permanente de 1,5 kN a cada nível no CC 1: Carga permanente e variável de 3 kN em cada nível no CC2: Ao vivo. As configurações adicionais em CC2 são ativadas para considerar automaticamente 25% da carga variável para a combinação de massas.
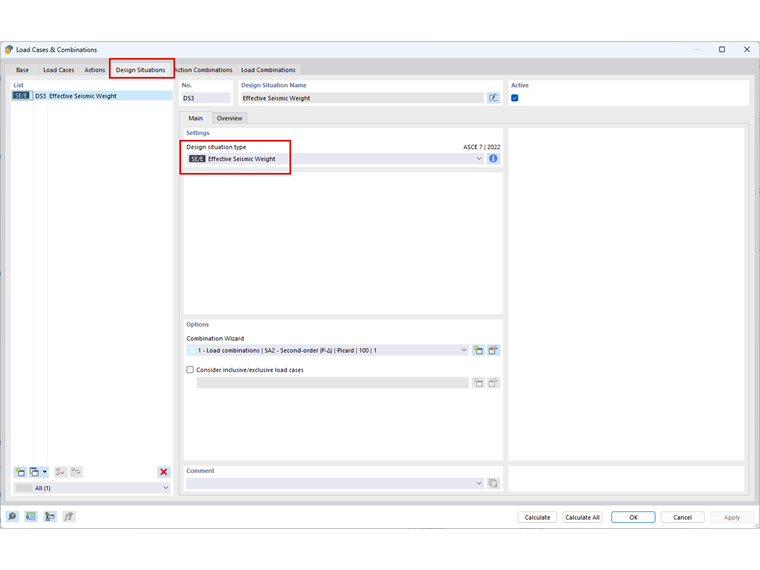
A situação de dimensionamento DS1: O peso sísmico efetivo é definido para criar automaticamente a combinação de massas CO1: D + 0,25L. Após a conversão da massa, é considerado um total de 1000 kg em cada nível na direção X para posterior análise sísmica.
O módulo Análise modal permite calcular as formas próprias e as massas modais efetivas de uma estrutura. É possível considerar um estado inicial, ao qual aplicará uma modificação de rigidez com base na definição dos casos de carga e das combinações de carga. São definidos dois casos de carga da análise modal. O primeiro é o CC3: Modal – sem modificações de rigidez para realizar a análise modal sem quaisquer alterações de rigidez.
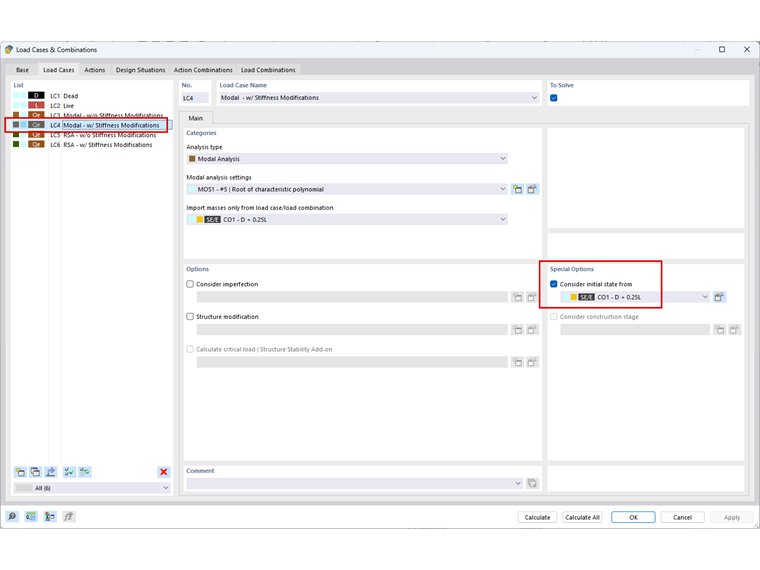
Para CC4: Modal – com modificações de rigidez, a opção considerar estado inicial está ativada. O caso de carga ou a combinação de cargas aqui importada deve considerar as cargas axiais de compressão mais elevadas da estrutura. Neste exemplo, a combinação de massas CO1 é utilizada para aproximar os efeitos de segunda ordem com as modificações de rigidez geométrica.
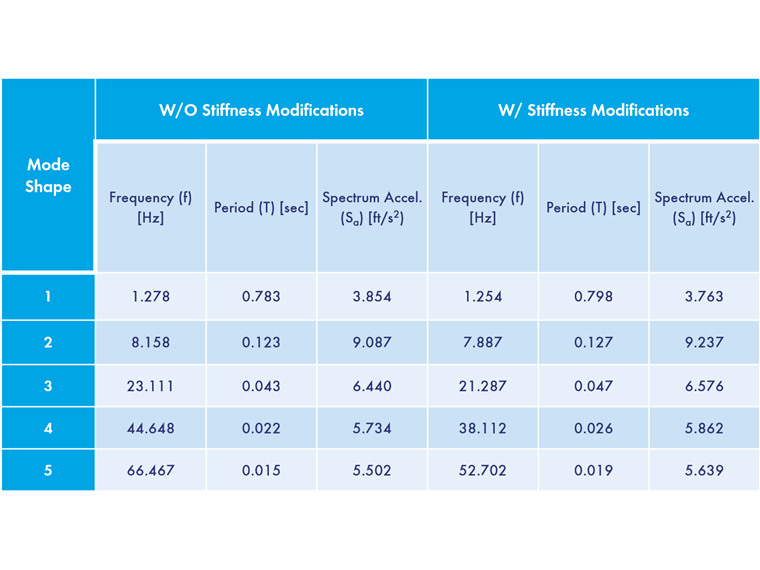
A tabela seguinte mostra as frequências naturais (f) [Hz] e os períodos naturais (T) [sec] calculados com e sem a matriz de rigidez geométrica Kg considerada.
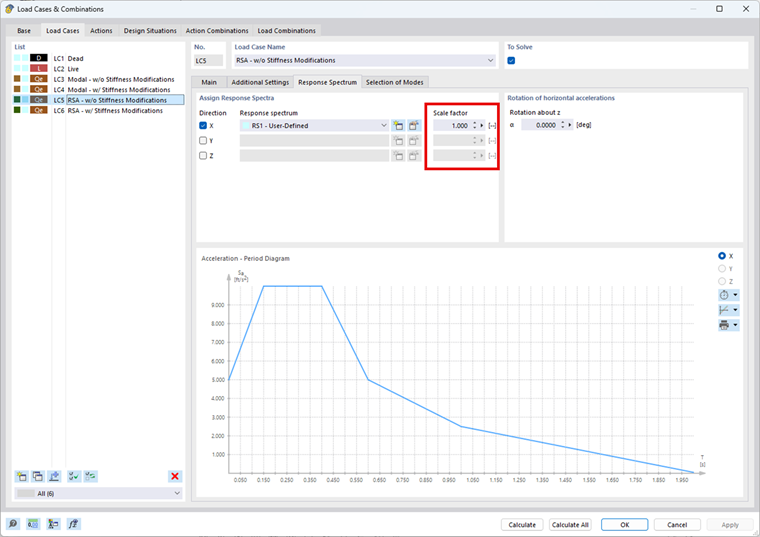
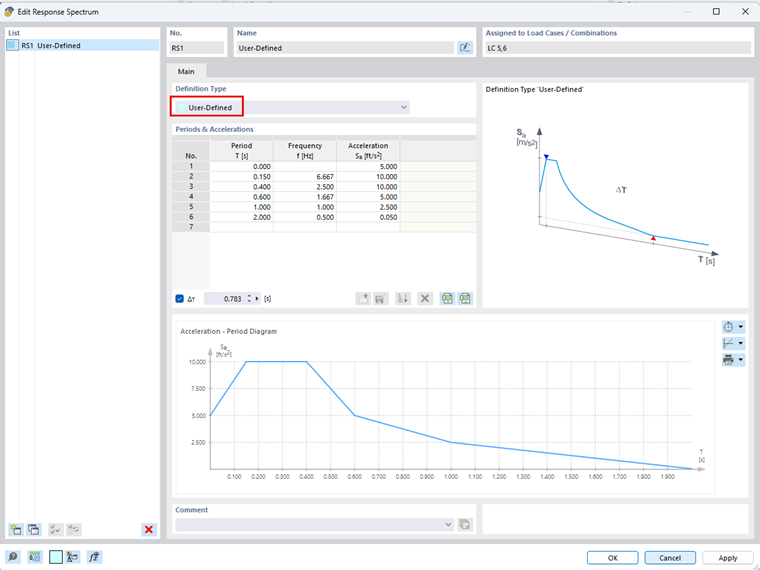
A análise do espectro de resposta multimodal utiliza as frequências naturais da estrutura para determinar os valores de aceleração a partir do espectro de resposta definido. Com base nestes valores de aceleração, o programa determina as forças internas do espectro de resposta. Para este exemplo, é apresentado um espectro de resposta definido pelo utilizador. Os valores de aceleração Sa [ft/s2 ] determinados a partir do espectro de resposta definido pelo utilizador para cada valor próprio estão listados na tabela acima.
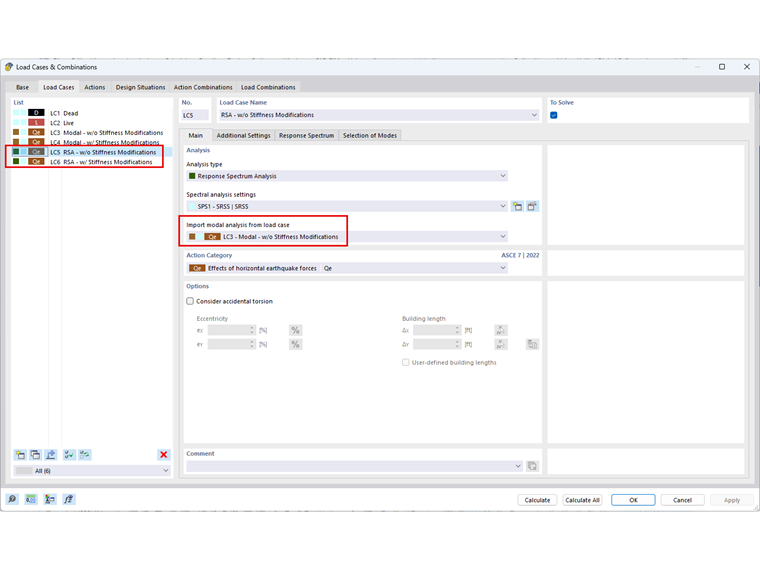
Para garantir a atribuição correta das frequências modificadas, tem de ser selecionada a análise modal desejada ao definir um caso de carga do espectro de resposta. Isto significa que, se a análise do espectro de resposta for considerar as modificações de rigidez geométrica, a análise modal relevante com as modificações de rigidez previamente definidas deve ser referenciada.
Ao aplicar forças de compressão axiais, a consideração da matriz de rigidez geométrica leva a frequências naturais mais baixas da estrutura. Isto pode causar valores de aceleração Sa mais baixos, como pode ser visto neste exemplo. Apenas uma modificação das frequências naturais não é suficiente para considerar a teoria de segunda ordem. De facto, isto pode levar a resultados inferiores, os quais podem estar incorretos. Portanto, é importante também utilizar a matriz de rigidez modificada ao calcular as forças internas e as deformações da estrutura. Na análise do espectro de resposta do RFEM, a rigidez modificada da análise modal é automaticamente utilizada para determinar os resultados da análise do espectro de resposta, quando selecionada. As deformações, os esforços internos e as reações de apoio determinados na análise de espectro de resposta com e sem a matriz de rigidez geométrica são apresentados na Figura 08.
_and_with_Stiffness_Modification_(bottom).png?mw=760&hash=a0656d7f5afcb25e57fe07073895766288787ecd)
A consideração da matriz de rigidez geométrica leva a deformações e esforços internos maiores. No entanto, as cargas de apoio resultantes são ligeiramente menores quando consideramos a matriz de rigidez geométrica.
Base de dados de conhecimento