INTRODUÇÃO
Este artigo fornece orientações sobre o dimensionamento de ligações resistentes ao momento de acordo com o Eurocódigo 3, focando-se em específico nas ligações de chapa de extremidade parafusada entre vigas e pilares em estruturas de vários andares. Ele faz referência a seções relevantes, figuras e tabelas da EN 1993-1-8 e outros padrões aplicáveis conforme necessário.
ABORDAGEM ANALÍTICA
O procedimento analítico é retirado de [1].
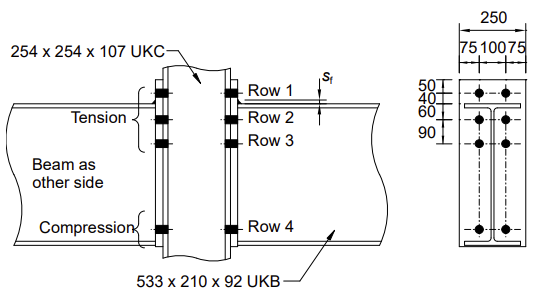
Configuração das ligações
| Coluna | 254x254x107 UKC | S275 |
| Viga | 533x210x92 UKB | S275 |
| Chapa de extremidade | 670x250x25 mm | S275 |
| Parafuso | M24 classe 8.8 | |
| Soldas | Cordões de solda: aba sf = 12 mm, alma sw = 8 mm |
Resistência T-Sub Equivalente
A resistência de T-Stub equivalente é avaliada separadamente para a chapa de extremidade e o banzo do pilar. As resistências são calculadas para três modos possíveis de rotura, e a resistência é considerada como o valor mínimo desses três modos.
A resistência de cálculo do banzo de T-Stub para cada um dos modos é fornecida abaixo.
Os modos de rotura são apresentados abaixo:
| onde | ||
| ℓeff,1 | é o comprimento efetivo de T-Stub equivalente para o Modo 1, considerado como o menor entre ℓeff,cp e ℓeff,nc | |
| ℓeff,2 | é o comprimento efetivo de T-Stub equivalente para o Modo 2, considerado como ℓeff,nc | |
| tf | espessura do banzo de T-Stub (= tp ou tfc) | |
| fy | é a tensão de cedência do banzo de T-Stub (ou seja, do pilar ou da chapa de extremidade) | |
| ∑Ft,Rd | é a resistência à tração total para os parafusos de T-Stub (= 2Ft,Rd para uma única fila) | |
| ew | = dw/4 | |
| dw | é o diâmetro do espaçador ou a largura entre os pontos da cabeça do parafuso | |
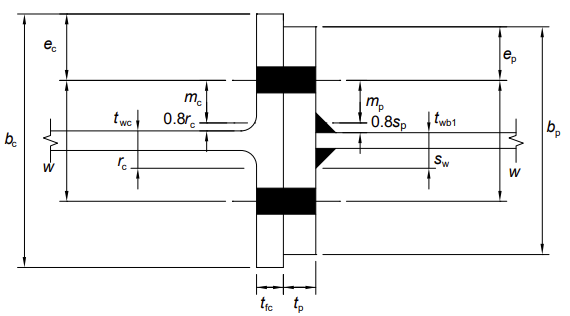
| m | é a distância conforme definido na figura acima | |
| n | é o mínimo de ec (a distância da borda do banzo do pilar), ep (a distância da borda da chapa de extremidade), 1.25 m (para a chapa de extremidade ou o banzo do pilar, conforme apropriado) |
Definição de resistência:
T-Stubs na zona de tração
PARAFUSO FILA 1
Banzo do pilar em flexão (sem chapa de reforço)
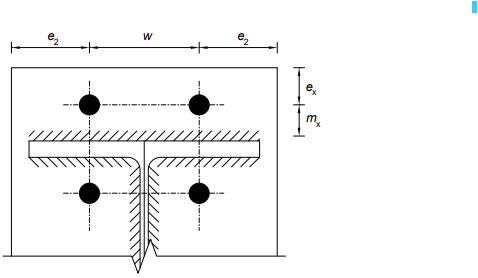
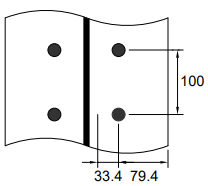
Considere a fila de parafusos 1 atuando sozinha. As dimensões principais são mostradas abaixo.
Placa de extremidade em flexão
Resumo do cálculo de resistência:
| Parâmetro | Unidade | Banzo do pilar em flexão (sem chapa de reforço) | Alma do pilar em tração transversal | Chapa de extremidade em flexão | Alma da viga em tração | |
| m | [mm] | 33.4 | - | = mx = 30.4 | - | |
| e | [mm] | = emin = 75 | - | e = 75, ex = 50 | - | |
| ℓeff,1 | [mm] | 210 | - | 125 | - | |
| ℓeff,2 | [mm] | 233 | - | 125 | - | |
| MODO 1 | ||||||
| n | [mm] | 41.8 | - | 38.0 | - | |
| tf | [mm] | 20.5 | - | 25 | - | |
| fy | [N/mm2] | 265 | - | 265 | - | |
| Mpl,1,Rd | [Nmm] | 5850x103 | - | 5180x103 | - | |
| dw | [mm] | 39.55 | - | - | - | |
| ew | [mm] | 9.9 | - | 9.9 | - | |
| FT,1,Rd | [kN] | 898 | - | 901 | - | |
| MODO 2 | ||||||
| Mpl,2,Rd | [Nmm] | 6490x103 | - | 5180x103 | - | |
| Ft,Rd | [N] | 203x103 | - | 203x103 | - | |
| Parafuso em uma fila | [pcs] | 2 | - | 2 | - | |
| ∑Ft,Rd | [N] | 406x103 | - | 406x103 | - | |
| FT,2,Rd | [kN] | 398 | - | 377 | - | |
| MODO 3 | ||||||
| FT,3,Rd | [kN] | 406 | - | 406 | - | |
| ω | [-] | - | 1.0 | - | ||
| beff,t,wc | [mm] | - | = ℓeff,2 = 233 | - | ||
| fy,wc | [N/mm2] | - | = fy,c = 265 | - | ||
| RESISTÊNCIA | Ft,fc,Rd | Ft,wc,Rd | Ft,ep,Rd | |||
| [kN] | 398 | 790 | 377 | |||
| NOTA | não é aplicável |
A resistência da fila de parafusos 1 é o menor valor das resistências mencionadas acima.
Portanto, Ft,1,Rd = min {Ft,fc,Rd = 398; Ft,wc,Rd = 790; Ft,ep,Rd = 377} = 377 kN.
PARAFUSO FILA 2
Em primeiro, considere a fila 2 isolada.
Chapa de extremidade em flexão
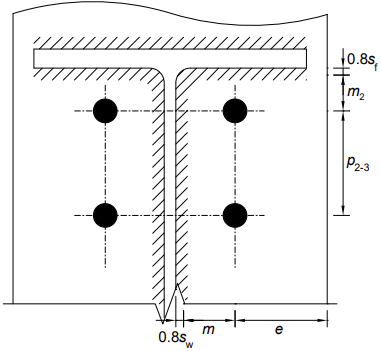
A fila de parafusos 2 é a primeira fila de parafusos abaixo do banzo da viga, considerada como a 'primeira fila de parafusos abaixo do banzo de tração da viga'. As dimensões principais para o T-Stub são apresentadas para o T-Stub do banzo do pilar na fila 1 e como mostrado abaixo (em elevação) para a fila 2.
Resumo do cálculo de resistência:
| Parâmetro | Unidade | Banzo do pilar em flexão | Alma do pilar em tração transversal | Chapa de extremidade em flexão | Alma da viga em tração | |
| m | [mm] | - | - | = mp = 38.6 | - | |
| m2 | [mm] | - | - | 34.8 | - | |
| e | [mm] | - | - | = ep = 75 | - | |
| ℓeff,1 | [mm] | - | - | 243 | - | |
| ℓeff,2 | [mm] | - | - | 290 | - | |
| MODO 1 | ||||||
| n | [mm] | - | - | 48.3 | - | |
| tf | [mm] | - | - | 25 | - | |
| fy | [N/mm2] | - | - | 265 | - | |
| Mpl,1,Rd | [Nmm] | - | - | 10.1x103 | - | |
| ew | [mm] | - | - | 9.9 | - | |
| FT,1,Rd | [kN] | - | - | 1291 | - | |
| MODO 2 | ||||||
| Mpl,2,Rd | [Nmm] | - | - | 12.0x106 | - | |
| Ft,Rd | [N] | - | - | 203x103 | - | |
| Parafuso em uma fila | [pcs] | - | - | 2 | - | |
| ∑Ft,Rd | [N] | - | - | 406x103 | - | |
| FT,2,Rd | [kN] | - | - | 502 | - | |
| MODO 3 | ||||||
| FT,3,Rd | [kN] | - | - | 406 | - | |
| ω | [-] | - | - | - | 1.0 | |
| beff,t,wc | [mm] | - | - | - | 243 | |
| twb | [mm] | - | - | - | 10.1 | |
| fy,wc | [N/mm2] | - | - | - | 675 | |
| RESISTÊNCIA | Ft,fc,Rd | Ft,wc,Rd | Ft,ep,Rd | Ft,wb,Rd | ||
| [kN] | 398 | 790 | 406 | 675 | ||
| NOTA | Como calculado para a fila de parafusos 1, Modo 2 | como calculado para a fila de parafusos 1 |
As resistências para a fila 2 acima consideram a atuação isolada da fila. No entanto, do lado do pilar, a resistência pode ser limitada pela resistência do grupo das filas 1 e 2. O grupo de resistência é considerada agora.
LINHAS 1 E 2 COMBINADAS
Banzo do pilar em flexão
Resumo do cálculo de resistência:
| Parâmetro | Unidade | Banzo do pilar em flexão | Alma do pilar em tração transversal | Chapa de extremidade em flexão | |
| m | [mm] | 33.4 | - | - | |
| ℓeff,1 | [mm] | 332 | - | - | |
| ℓeff,2 | [mm] | 332 | - | - | |
| MODO 1 | |||||
| n | [mm] | 41.8 | - | - | |
| tf | [mm] | 20.5 | - | - | |
| fy | [N/mm2] | 265 | - | - | |
| Mpl,1,Rd | [Nmm] | 9.24x103 | - | - | |
| ew | [mm] | 9.9 | - | - | |
| FT,1,Rd | [kN] | 1420 | - | - | |
| MODO 2 | |||||
| Mpl,2,Rd | [Nmm] | 9.24x106 | - | - | |
| Ft,Rd | [N] | 203 | - | - | |
| Parafusos | [pcs] | 4 | - | - | |
| ∑Ft,Rd | [N] | 812 | - | - | |
| FT,2,Rd | [kN] | 697 | - | - | |
| MODO 3 | |||||
| FT,3,Rd | [kN] | 812 | - | - | |
| ω | [-] | - | 1.0 | - | |
| beff,t,wc | [mm] | - | 332 | - | |
| twb | [mm] | - | 12.8 | - | |
| fy,wc | [N/mm2] | - | 265 | - | |
| RESISTÊNCIA | Ft,fc,Rd | Ft,wc,Rd | Ft,ep,Rd | ||
| [kN] | 697 | 1126 | - | ||
| NOTA | Não há modo de grupo para a chapa de extremidade |
A resistência das fileiras de parafusos 1 e 2 é o menor valor das resistências Banzo do pilar em flexão e Alma do pilar em tração, ou seja, Ft,1-2,Rd = min {Ft,fc,Rd = 697; Ft,wc,Rd = 1126} = 697 kN.
Portanto, a resistência da fila de parafusos 2 no lado do pilar é limitada a Ft2,c,Rd = Ft,1-2,Rd - Ft1,Rd = 697 - 377 = 320 kN.
A resistência da fila de parafusos 2 é o menor valor das resistências: Banzo do pilar em flexão Ft,fc,Rd = 398 kN, Alma do pilar em tração Ft,wc,Rd = 790 kN, Alma da viga em tração Ft,wb,Rd = 675 kN, Chapa de extremidade em flexão Ft,ep,Rd = 406 kN e Lado do pilar, como parte do grupo, Ft2,c,Rd = 320 kN. Portanto, a resistência da fila de parafusos 2 Ft,2,Rd = 320 kN.
PARAFUSO FILA 3
Primeiro, considere a fila 3 isolada.
Resumo do cálculo de resistência:
| Parâmetro | Unidade | Banzo do pilar em flexão | Alma do pilar em tração transversal | Chapa de extremidade em flexão | Alma da viga em tração | |
| e | [mm] | - | - | = ep = 75 | - | |
| m | [mm] | - | - | 38.6 | - | |
| ℓeff,1 | [mm] | - | - | 248 | - | |
| ℓeff,2 | [mm] | - | - | 248 | - | |
| MODO 1 | ||||||
| n | [mm] | - | - | 48.3 | - | |
| tf | [mm] | - | - | 25 | - | |
| fy | [N/mm2] | - | - | 265 | - | |
| Mpl,1,Rd | [Nmm] | - | - | 10.1x106 | - | |
| ew | [mm] | - | - | 9.9 | - | |
| FT,1,Rd | [kN] | - | - | 1291 | - | |
| MODO 2 | ||||||
| Mpl,2,Rd | [Nmm] | - | - | 10.3x106 | - | |
| Ft,Rd | [N] | - | - | 203 | - | |
| Parafusos | [pcs] | - | - | 2 | - | |
| ∑Ft,Rd | [N] | - | - | 406 | - | |
| FT,2,Rd | [kN] | - | - | 463 | - | |
| MODO 3 | ||||||
| FT,3,Rd | [kN] | - | - | 406 | - | |
| beff,t,wb | [mm] | - | - | - | = beff,1 = 243 | |
| twb | [mm] | - | - | - | 10.1 | |
| RESISTÊNCIA | Ft,fc,Rd | Ft,wc,Rd | Ft,ep,Rd | Ft,wb,Rd | ||
| [kN] | 790 | 790 | 406 | 675 | ||
| NOTA |
|
Como calculado para as filas de parafusos 1 e 2 |
As resistências para as filas 2 e 3 acima consideram a resistência da fila atuando sozinha. No entanto, do lado do pilar , a resistência pode ser limitada pela resistência do grupo das filas 1, 2 e 3, ou pelo grupo das filas 2 e 3. Do lado da viga, a resistência pode ser limitada pelo grupo das filas 2 e 3. Essas resistências de grupo são agora consideradas.
PARAFUSOS 1, 2 E 3 COMBINADOS
Banzo do pilar em flexão
Os padrões circulares e não circulares são os seguintes:
Resumo do cálculo de resistência:
| Parâmetro | Unidade | Banzo do pilar em flexão | Alma do pilarem tração transversal | |
| ℓeff,1 | [mm] | 422 | - | |
| ℓeff,2 | [mm] | 422 | - | |
| MODO 1 | ||||
| m | [mm] | 33.4 | - | |
| n | [mm] | 41.8 | - | |
| ew | [mm] | 9.9 | - | |
| tf | [mm] | 20.5 | - | |
| fy | [N/mm2] | 265 | - | |
| Mpl,1,Rd | [Nmm] | 11.7x106 | - | |
| FT,1,Rd | [kN] | 1797 | - | |
| MODO 2 | ||||
| Mpl,2,Rd | [Nmm] | 11.7x106 | - | |
| Ft,Rd | [kN] | 203 | - | |
| Parafusos | [pcs] | 6 | - | |
| ∑Ft,Rd | [kN] | 1218 | - | |
| FT,2,Rd | [kN] | 988 | - | |
| MODO 3 | ||||
| FT,3,Rd | [kN] | 1218 | - | |
| ω | [-] | - | 1.0 | |
| beff,t,wc | [mm] | - | 422 | |
| twc | [mm] | - | 12.8 | |
| RESISTÊNCIA | Ft,fc,Rd | Ft,wc,Rd | ||
| [kN] | 988 | 1431 |
A resistência das filas de parafusos 1, 2 e 3 combinadas, do lado do pilar, é o menor valor das resistências Banzo do pilar em flexão e Alma do pilar em tração, que é 988 kN.
Portanto, a resistência da fila de parafusos 3 no lado da coluna é limitada a: Ft3,c,Rd = Ft1-3,Rd - Ft1-2,Rd = 988 - 697 = 291 kN.
LINHAS 2 E 3 COMBINADAS
Resumo do cálculo de resistência:
| Parâmetro | Unidade | Lado da coluna - banzo em flexão | Alma do pilar em tração transversal | Lado da viga - chapa de extremidade em flexão | Viga em tração | |
| m | [mm] | 33.4 | - | 38.6 | - | |
| n | [mm] | 41.8 | - | 48.3 | - | |
| ew | - | - | 9.9 | - | ||
| ℓeff,1 | [mm] | 323 | - | 379 | - | |
| ℓeff,2 | [mm] | 323 | - | 379 | - | |
| MODO 1 | (linhas 2 + 3) | |||||
| Mpl,1,Rd | [Nmm] | 9.24x103 | 9.0x106 | 15.7x106 | - | |
| FT,1,Rd | [kN] | 1383 | - | 2007 | - | |
| MODO 2 | (linhas 2 + 3) | |||||
| Mpl,2,Rd | [Nmm] | 9.0x106 | - | 15.7x106 | - | |
| Ft,Rd | [kN] | 203 | - | 203 | - | |
| Parafusos | [pcs] | 4 | - | 4 | - | |
| ∑Ft,Rd | [kN] | 812 | - | 812 | - | |
| FT,2,Rd | [kN] | 691 | - | 813 | - | |
| MODO 3 | (linhas 2 + 3) | |||||
| FT,3,Rd | [kN] | 1218 | - | 812 | - | |
| ω | [-] | - | 1.0 | - | - | |
| beff,t,wc | [mm] | - | 323 | - | - | |
| twb | [mm] | - | 12.8 | - | - | |
| fy,wc | [N/mm2] | - | 265 | - | - | |
| RESISTÊNCIA | Ft,fc,Rd | Ft,wc,Rd | Ft,ep,Rd | |||
| [kN] | 691 | 1096 | 812 | - | ||
| NOTA | não aplicável |
A resistência das filas de parafusos 2 e 3 combinadas, do lado da viga, é Chapa de extremidade em flexão Ft,ep,Rd = 812 kN. Portanto, do lado da viga Ft2-3,Rd = 812 kN. A resistência da fila de parafusos 3 do lado da viga é limitada a Ft3,b,Rd = Ft2-3,Rd - Ft2,Rd = 812 - 320 = 492 kN.
A resistência das filas de parafusos 2 e 3 combinadas, do lado do pilar, é Banzo do pilar em flexão Ft,fc,Rd = 691 kN, Alma do pilar em tração Ft,wc,Rd = 1096 kN, portanto, do lado da coluna Ft2-3,Rd = 691 kN.
Assim, a resistência da fila de parafusos 3 do lado do pilar é limitada a Ft3,b,Rd = Ft2-3,Rd - Ft2,Rd = 691 - 320 = 371 kN.
Resumo
A resistência da fila de parafusos 3 é o menor valor entre as seguintes resistências: Banzo do pilar em flexão Ft,fc,Rd = 398 kN, Alma do pilarem tração Ft,wc,Rd = 790 kN, Alma da viga em tração Ft,wb,Rd = 675 kN, Chapa de extremidade em flexão Ft,ep,Rd = 406 kN, Lado do pilar como parte de um grupo com 2 e 1 Ft3,c,Rd = 291 kN, Lado do pilar como parte de um grupo com 2 Ft3,c,Rd = 371 kN, Lado da viga como parte de um grupo com 2 Ft3,b,Rd = 492 kN. Portanto, a resistência da fila de parafusos 3 é Ft3,Rd = 291 kN.
RESUMO DAS RESISTÊNCIAS À TRAÇÃO
A derivação das resistências efetivas das filas de tração acima pode ser resumida em forma de tabela, conforme mostrado abaixo.
Resistências das filas Ftr,Rd:
| Banzo do pilar | Alma do pilar | Chapa de extremidade | Alma da viga | Mínimo | Resistência efetiva | ||
| Fila 1, sozinha | 398 | 790 | 377 | N/A | 377 | 377 | |
| Fila 2, sozinha | 398 | 790 | 406 | 675 | 398 | ||
| Fila 2, com fila 1 | 697 | 1126 | N/A | N/A | 697 | ||
| Fila 2 | 697 - 377 | 320 | |||||
| Fila 3, sozinha | 398 | 790 | 406 | 675 | 309 | ||
| Fila 3, com fila 1 e 2 | 988 | 1431 | N/A | N/A | 988 | ||
| Fila 3 | 988 - 697 | 291 | |||||
| Fila 3, com fila 2 | 691 | 1096 | 812 | 1052 | 691 | ||
| Fila 3 | 691 - 320 |
Zona de Compressão
Alma do pilar em compressão transversal
A resistência de cálculo de uma alma do pilar não reforçada em compressão transversal é determinada como segue:
| onde | ||
| s | = rc = 12.7 mm para seções de pilar em I e H laminadas a quente | |
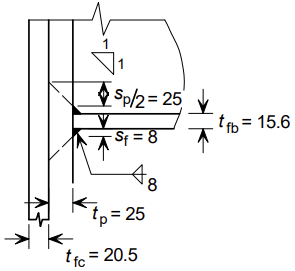
| sp | é o comprimento obtido pela dispersão a 45° através da chapa de extremidade; sp = 2 tp = 50 mm | |
| ex | é a distância de extremidade medida a partir do centro do reforço da linha 1; ex = 50 mm | |
| x | é o espaçamento acima do banzo da viga medida a partir do centro do reforço; x = 40 mm | |
| sf |
|
|
| hp | é a profundidade da chapa de extremidade; hp ≥ ex + x + hb + sf + tp = 656 mm → hp = 670 mm | |
| beff,c,wc | para uma chapa de extremidade parafusada; beff,c,wc = tfb + 2 sf + 5 (tfc + s) + sp = 248 mm | |
| ρ | é o fator de redução para a encurvadura da placa, depende da placa; ρ = 1.0 | |
| ω | = 1.0 | |
| kwc | é um fator de redução que considera a compressão na alma do pilar; kwc = 1.0 |
Portanto, Fc,wc,Rd = 841 kN.
Banzo e alma da viga em compressão
A resistência de cálculo resultante de um banzo de viga e a zona de compressão adjacente da alma é determinada utilizando:
| onde | ||
| Mc,Rd | é a resistência de cálculo da viga; supondo que a força de corte de cálculo na viga não reduza Mc,Rd, portanto, Mc,Rd = 649 kN | |
| h | = hb = 533.1 mm | |
| tfb | = 15.6 mm |
Assim, Fc,fb,Rd = 1254 kN.
Resumo: resistência da zona de compressão
Alma do pilar em compressão transversal Fc,wc,Rd = 841 kN, Banzo da viga e alma em compressão Fc,fb,Rd = 1254 kN.
Resistência ao corte da placa de alma do pilar
A resistência ao corte plástico de uma alma não reforçada é dada por:
A resistência não é avaliada aqui, pois não há força de corte na alma porque os momentos das vigas são iguais e opostos.
Resistência ao Momento
RESISTÊNCIA EFETIVA DAS FILAS DE PARAFUSOS
As resistências efetivas de cada uma das três fileiras de parafusos na zona de tração são:
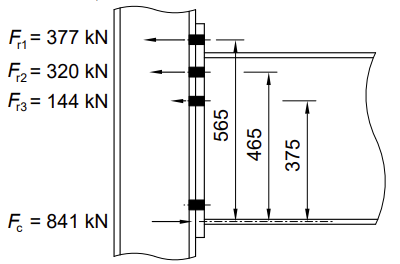
Ft1,Rd = 377 kN, Ft2,Rd = 320 kN, Ft3,Rd = 291 kN.
As resistências efetivas devem ser reduzidas se a resistência de uma das fileiras superiores exceder 1.9 Ft,Rd = 1.9 x 203 = 386 kN.
Desta forma, não é necessária nenhuma redução.
EQUILÍBRIO DE FORÇAS
A soma das forças de tração, juntamente com qualquer compressão axial na viga, não pode exceder a resistência da zona de compressão.
Da mesma forma, o a força de corte de cálculo não pode exceder a resistência ao corte do painel de alma do pilar. Isso não é relevante neste exemplo, pois os momentos nas vigas idênticas são iguais e opostos.
Para o equilíbrio horizontal ∑Ftr,Rd + NEd = Fc,Rd. Neste exemplo, não há compressão axial. Assim, ∑Ftr,Rd = Fc,Rd.
Aqui, a resistência à tração efetiva total ∑Ftr,Rd = 377 + 320 + 291 = 988 kN, que excede a resistência à compressão Fс,Rd = 841 kN.
Para alcançar o equilíbrio, as resistências efetivas são reduzidas, começando na fileira mais baixa, até que o equilíbrio seja alcançado. Redução necessária de 988 - 841 = 147 kN.
Toda essa redução pode ser conseguida reduzindo a resistência da fila inferior. Assim, Ft3,Rd = 291 - 147 = 144 kN.
RESISTÊNCIA AO MOMENTO DAS FORÇAS
A resistência ao momento da ligação viga-pilar Mj,Rd:
Considerando o centro de compressão como a espessura média do banzo de compressão da viga, hr1 = 565 mm, hr2 = 465 mm, hr3 = 375 mm. Assim, a resistência ao momento da ligação viga-pilar é:
Mj,Rd = 416 kNm.
Resistência ao corte vertical
RESISTÊNCIA DO GRUPO DE PARAFUSOS
A resistência ao corte de um parafuso M24 classe 8.8 não pré-carregado em corte simples é Fv,Rd = 136 kN, Fb,Rd = 200 kN (em 20 mm de espessura). Assim, Fv,Rd governa.
A resistência ao corte das fileiras superiores pode ser conservadoramente considerada como 28% da resistência ao corte sem tração (assumindo que esses parafusos são totalmente utilizados em tração). Assim, a resistência ao corte de todas as 4 fileiras é (2 + 6 x 0.28) 136 = 3.68 x 136 = 500 kN.
Dimensionamento de soldaduras
A abordagem simples requer que as soldas no banzo de tração e alma sejam de força total, enquanto a solda no banzo de compressão é apenas de tamanho nominal, assumindo que foi preparada com uma serra de extremidade cortada.
SOLDAS DO BANZO DE TRAÇÃO DA VIGA
É providenciada uma solda de força total através de cordões de soldadura simétricos com uma espessura total pelo menos igual à espessura do banzo. A espessura total requerida é tfb/2 = 15.6/2 = 7.8 mm. A espessura da soldadura fornecida é af = 12/√2 = 8.5 mm, o que é adequado.
SOLDAS DO BANZO DE COMPRESSÃO DA VIGA
É providenciado um cordão de soldadura nominal em cada lado do banzo da viga. Um cordão de solda com comprimento de perna de 8 mm será satisfatório.
SOLDAS DA ALMA DA VIGA
Para conveniência, uma solda de força total é providencia à alma.
Tamanho da espessura da solda necessário é tfw/2 = 10.2/2 = 5.1 mm.
A espessura da solda fornecida é ap = 8/√2 = 5.7 mm, o que é adequado.
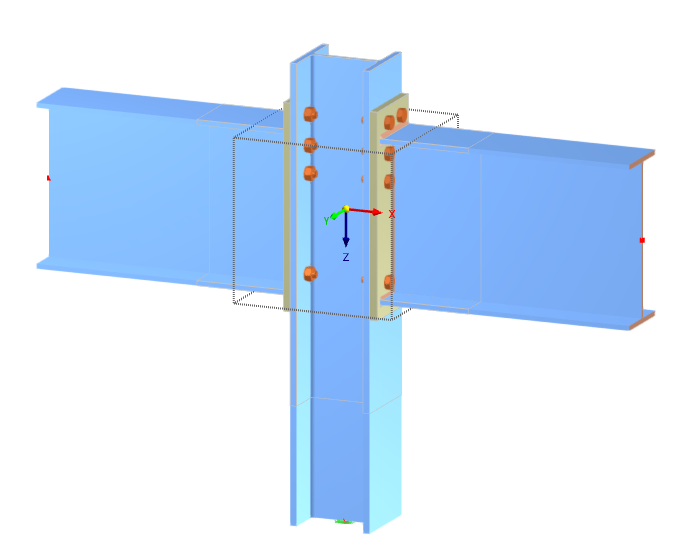
ANÁLISE EF DO COMPONENTE
O dimensionamento foi realizado utilizando o módulo de ligações de aço para o RFEM 6.
O módulo de ligações de aço permite a análise de ligações com base em um modelo EF. A entrada e a avaliação do resultados estão totalmente integradas à interface do utilizador do software de AEF estrutural RFEM, tornando o processo de dimensionamento intuitivo e rápido.
Configuração da Ligação
| Coluna | 254x254x107 UKC | S275 |
| Viga | seção definida parametricalmente | |
| hb = 533.1 mm, bb = 209.3 mm, twb = 10.1 mm, tfb = 15.6 mm | S275 | |
| Chapa de extremidade | 670x250x25 mm | S275 |
| Parafuso | M24 classe 8.8 | |
| Soldas | Cordão de soldadura do banzo superior sf1 = 8.5 mm, banzo inferior sf2 = 5.7 mm, alma sw = 5.7 mm |
Resultados do módulo de ligações de aço
O módulo de ligações de aço para RFEM 6 melhora as capacidades do software ao permitir que os engenheiros analisem ligações de aço com a precisão de um modelo de elemento finito (EF). Esta ferramenta avançada permite a visualização detalhada de todos os resultados essenciais diretamente no modelo EF, fornecendo uma visão clara e abrangente do desempenho das ligações de aço sujeitos a várias cargas e condições.
Inclui a visualização de tensões equivalentes e deformações plásticas dentro da ligação de aço. Ao mostrar tanto tensões equivalentes quanto deformações plásticas, o RFEM oferece uma compreensão mais abrangente do comportamento da ligação em condições do mundo real, garantindo que o dimensionamento seja seguro e eficiente.
TENSÕES EQUIVALENTES
As tensões equivalentes fornecem uma visão clara da distribuição de tensões gerais, ajudando os engenheiros a identificar possíveis pontos de rotura causados por concentrações excessivas de tensões. Essas tensões são essenciais para entender a capacidade resistente da ligação.
Aqui, podem ser vista a distribuição de tensões no banzo do pilar da coluna e na chapa de extremidade da viga.
DEFORMAÇÃO PLÁSTICA
As placas na ligação são dimensionadas plasticamente comparando a deformação plástica existente com a deformação plástica permitida. A configuração definida por defeito é 5%, de acordo com EN 1993‑1‑5, Anexo C. Abaixo encontra-se a deformação plástica na ligação :
ANÁLISE TENSÃO-DEFORMAÇÃO
Conclusões
O artigo apresenta dois métodos para o dimensionamento de ligações viga-pilar. O método analítico é complexo e difícil para ser realizado manualmente, especialmente quando se trata de otimização. Envolve calcular as resistências de cada componente e compará-las com as forças atuantes nesses componentes.
O segundo método é a abordagem CBFEM, implementada no módulo de ligações de aço do RFEM 6. Neste método, a ligação é montada e as forças para análise são derivadas do modelo EF principal. A junta montada é então verificada sob as forças aplicadas através da análise tensão-deformação das placas de aço. Além disso, o dimensionamento das soldaduras e reforços é realizado de acordo com as normas EN relevantes.
Embora o método analítico seja amplamente utilizado, o segundo método é muito mais rápido, fornecendo resultados precisos enquanto reduz significativamente o tempo de cálculo. Também permite fácil e rápida otimização.
Abaixo é apresentada uma comparação dos resultados.
A resistência ao momento Mj,Rd calculada utilizando a abordagem analítica é de 416 kNm, enquanto o valor do CBFEM no módulo de ligações de aço é de 415 kNm. A diferença é inferior a 1%, com Δ = -0.24%, ilustrando a confiabilidade e precisão do método CBFEM implementado no módulo de ligações de aço.
O modelo pode ser encontrado abaixo:
REFERÊNCIAS
[1] Brown, D., Iles, D., Brettle, M., Malik, A., e BCSA/SCI Connections Group. (2013). Juntas em construção de aço: Juntas resistentes a momento para Eurocódigo 3. Vol BCSA/SCI Connections Group. Londres: The British Constructional Steelwork Association Limited.