626x

001938

01.04.2025

Assemblage à par platine d’about boulonnée non raidie

Cet article examine un assemblage par platine d’about non raidie, un assemblage en acier couramment utilisée dans le bâtiment. Les calculs analytiques basés sur les directives de l’Eurocode 3 sont comparés aux résultats obtenus avec le module complémentaire Assemblages acier dans RFEM 6.
L’accent est mis sur l’évaluation de la précision et de la fiabilité de la méthode CBFEM dans la représentation du comportement structurel et des réponses de charge dans les structures en acier. Cette étude vise à approfondir la compréhension de la performance des logiciels MEF, en fournissant des connaissances pratiques très utiles pour les professionnels du génie civil.

INTRODUCTION

Cet article présente des conseils sur la vérification d’assemblages résistants aux moments selon l’Eurocode 3, ciblant spécifiquement les assemblage par platine d’about boulonnée entre poutres et poteaux dans des portiques à plusieurs étages. Il fait référence aux sections, figures et tableaux pertinents de l’EN 1993-1-8, et d’autres normes applicables si nécessaire.

APPROCHE ANALYTIQUE

La procédure analytique est issue de [1].

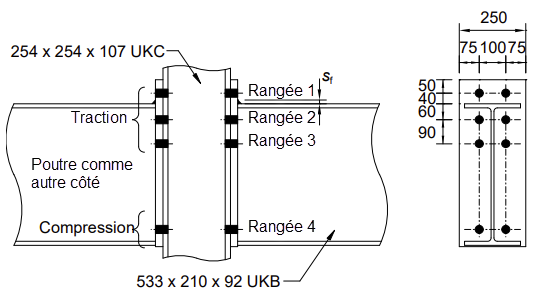
Configuration de l’assemblage

Illustration d’un assemblage boulonné en acier avec dimensions et détails de configuration précis.

Diagramme de vérification d’assemblages en acier

Poteau	254x254x107 UKC	S275
Poutre	533x210x92 UKB	S275
Platine d’about	670x250x25 mm	S275
Boulon	M24 classe 8.8
Soudures	Soudures d’angle: semelle s_f = 12 mm, âme s_w = 8 mm

Résistance du tronçon en T équivalent

La résistance des tronçons en T équivalents est évaluée séparément pour la platine d’about et la semelle du poteau. Les résistances sont calculées pour trois modes de rupture possibles, et la résistance est prise comme la plus petite des valeurs pour ces trois modes.

La résistance de calcul de la semelle de T-stub pour chacun des modes est donnée ci-dessous.

Interface technique affichant les résultats de simulation pour les modes de rupture des assemblages acier.

Modes de rupture dans les assemblages acier

Les modes de rupture sont présentés ci-dessous :

\begin{array}{l} Mode 1. Fluage complète de la semelle \\ F_{T, 1, R d} = \begin{matrix} (8 n - 2 e_{w}) M_{p l, 1, R d} \\ 2 m n - e_{w} (m + n) \end{matrix} \\ \begin{array}{l} Mode 2. Défaillance des boulons avec fluage de la semelle \\ F_{T, 2, R d} = \begin{array}{c} 2 M_{p l, 2, R d} + n (\sum F_{t, R d}) \\ m + n \end{array} \\ \begin{array}{l} Mode 3. Défaillance des boulons \\ F_{T, 3, R d} = \sum F_{t, R d} \end{array} \end{array} \end{array}

Modes de rupture

\begin{matrix} \begin{matrix} M_{p l, 1, R d} = \begin{array}{c} 0.25 \sum l_{e f f, 1} t_{f}^{2} f_{y} \\ γ_{M 0} \end{array}, \\ M_{p l, 2, R d} = \begin{array}{c} 0.25 \sum l_{e f f, 2} t_{f}^{2} f_{y} \\ γ_{M 0} \end{array} . \end{matrix} \end{matrix}

Moments de résistance plastique d’éclisse en T équivalente pour les modes 1 et 2

où
ℓ_eff,1	est la longueur efficace du tronçon en T équivalent pour le mode 1, prise comme le minimum entre ℓ_eff,cp et ℓ_eff,nc
ℓ_eff,2	est la longueur efficace du tronçon en T équivalent pour le mode 2, prise comme ℓ_eff,nc
t_f	est l’épaisseur de la semelle du tronçon en T (= t_p ou t_fc)
f_y	est la limite d’élasticité de la semelle du tronçon en T (c’est-à-dire du poteau ou de la platine d’about)
∑F_t,Rd	est la résistance totale en traction pour les boulons dans le tronçon en T (= 2F_t,Rd pour une seule rangée)
e_w	= d_w/4
d_w	est le diamètre de la rondelle ou la largeur entre les points de la tête de boulon
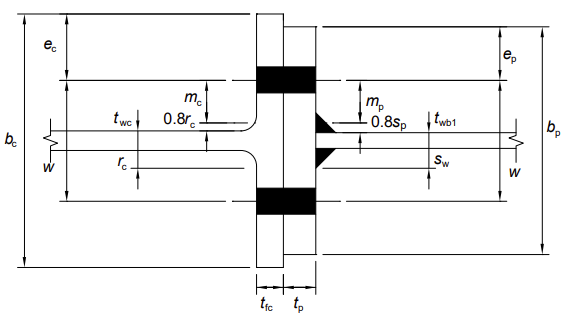
m	est la distance telle que définie dans la figure ci-dessus
n	est le minimum de e_c (la distance de rive de la semelle du poteau), e_p (la distance de rive de la platine d’about), 1,25 m (pour la platine d’about ou la semelle du poteau, selon le cas)

Définition de la résistance :

\begin{array}{l} Resistance of column flange in bending \\ F_{t, f c, R d} = \min {F_{T, 1, R d}, F_{T, 2, R d}, F_{T, 3, R d}} \\ \begin{array}{l} Resistance of an unstiffened column web to transverse tension \\ F_{t, w c, R d} = \begin{array}{c} ω b_{e f f, t, w c} t_{w c} f_{y, w c} \\ γ_{M 0} \end{array} \\ Resistance of the end plate in bending \\ F_{t, e p, R d} = \min {F_{T, 1, R d}, F_{T, 2, R d}, F_{T, 3, R d}} \\ \begin{matrix} \begin{array}{l} Resistance of the beam web \\ F_{t, w b, R d} = \begin{array}{c} b_{e f f, t, w b} t_{w b} f_{y, b} \\ γ_{M 0} \end{array} \end{array} \end{matrix} \end{array} \end{array}

Résistance des semelles de poteau en flexion

Tronçons en T de la zone en traction

RANGÉE DE BOULONS 1
Semelle du poteau en flexion (sans plaque d’appui)
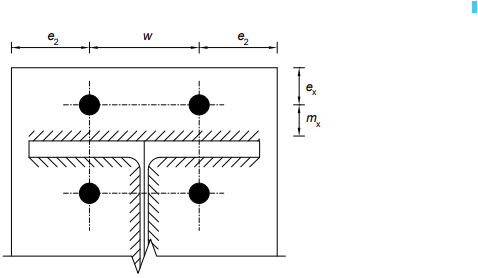
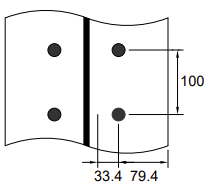
Considérez la rangée de boulons 1 seule. Les dimensions clés sont présentées ci-dessous.

Détail d’assemblage en acier illustrant un composant tronçon en T en zone de traction

Détail du tronçon en T de zone en traction

Platine d’about en flexion

Dimensions clés pour la première rangée du tronçon en T et le module complémentaire Assemblages acier dans RFEM 6

Aperçu des dimensions clés du tronçon de poutre en T

Résumé du calcul de la résistance :

Paramètre	Unité	Semelle de poteau en flexion (sans plaque d’appui)	Ame du poteau en traction transversale	Platine d’about en flexion	Ame de la poutre en traction
m	[mm]	33.4	-	= m_x = 30.4	-
e	[mm]	= e_min = 75	-	e = 75, e_x = 50	-
ℓ_eff,1	[mm]	210	-	125	-
ℓ_eff,2	[mm]	233	-	125	-

MODE 1
n	[mm]	41.8	-	38.0	-
t_f	[mm]	20.5	-	25	-
f_y	[N/mm²]	265	-	265	-
M_pl,1,Rd	[Nmm]	5850x10³	-	5180x10³	-
d_w	[mm]	39,55	-	-	-
e_w	[mm]	9,9	-	9,9	-
F_T,1,Rd	[kN]	898	-	901	-

MODE 2
M_pl,2,Rd	[Nmm]	6490x10³	-	5180x10³	-
F_t,Rd	[N]	203x10³	-	203x10³	-
Boulon en une rangée	[pcs]	2	-	2	-
∑F_t,Rd	[N]	406x10³	-	406x10³	-
F_T,2,Rd	[kN]	398	-	377	-

MODE 3
F_T,3,Rd	[kN]	406	-	406	-

ω	[-]	-	1.0	-
b_eff,t,wc	[mm]	-	= ℓ_eff,2 = 233	-
f_y,wc	[N/mm²]	-	= f_y,c = 265	-

RÉSISTANCE		F_t,fc,Rd	F_t,wc,Rd	F_t,ep,Rd
	[kN]	398	790	377
NOTE					n’est pas applicable

La résistance de la rangée de boulons 1 est la valeur minimale des résistances mentionnées ci-dessus.
Donc, F_t,1,Rd = min {F_t,fc,Rd = 398; F_t,wc,Rd = 790; F_t,ep,Rd = 377} = 377 kN.

RANGÉE DE BOULONS 2
Tout d’abord, considérez la rangée 2 seule.

Platine d’about en flexion
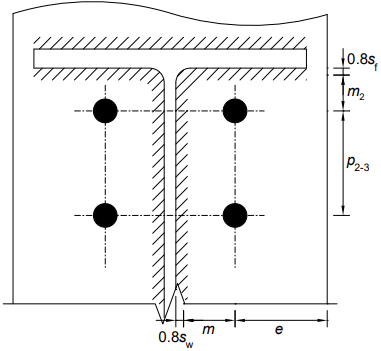
La rangée de boulons 2 est la première rangée de boulons sous la semelle de la poutre, considérée comme la « première rangée de boulons sous la semelle en traction de la poutre ». Les dimensions clés pour le tronçons en T sont montrées pour le tronçons en T de la semelle de poteau à la rangée 1 et comme illustré ci-dessous (en élévation) pour la rangée 2.

Diagramme des dimensions clés d’un T-stub en rangée 2 pour une analyse d’assemblage acier

Dimension de poutre en T ligne 2

Résumé du calcul de la résistance :

Paramètre	Unité	Semelle du poteau en flexion	Ame du poteau en traction transversale	Platine d’about en flexion	Ame de la poutre en traction
m	[mm]	-	-	= m_p = 38.6	-
m₂	[mm]	-	-	34.8	-
e	[mm]	-	-	= e_p = 75	-
ℓ_eff,1	[mm]	-	-	243	-
ℓ_eff,2	[mm]	-	-	290	-

MODE 1
n	[mm]	-	-	48.3	-
t_f	[mm]	-	-	25	-
f_y	[N/mm²]	-	-	265	-
M_pl,1,Rd	[Nmm]	-	-	10.1x10³	-
e_w	[mm]	-	-	9,9	-
F_T,1,Rd	[kN]	-	-	1291	-

MODE 2
M_pl,2,Rd	[Nmm]	-	-	12.0x10⁶	-
F_t,Rd	[N]	-	-	203x10³	-
Boulon en une rangée	[pcs]	-	-	2	-
∑F_t,Rd	[N]	-	-	406x10³	-
F_T,2,Rd	[kN]	-	-	502	-

MODE 3
F_T,3,Rd	[kN]	-	-	406	-

ω	[-]	-	-	-	1.0
b_eff,t,wc	[mm]	-	-	-	243
t_wb	[mm]	-	-	-	10.1
f_y,wc	[N/mm²]	-	-	-	675

RÉSISTANCE		F_t,fc,Rd	F_t,wc,Rd	F_t,ep,Rd	F_t,wb,Rd
	[kN]	398	790	406	675
NOTE	telle que calculée pour la rangée de boulons 1, mode 2	telle que calculée pour la rangée de boulons 1

Les résistances pour la rangée 2 ci-dessus considèrent toutes la rangée agissant seule. Cependant, du côté du poteau, la résistance peut être limitée par la résistance du groupe des rangées 1 et 2. La résistance du groupe sera maintenant prise en compte.

RANGÉES 1 ET 2 COMBINÉES
Semelle du poteau en flexion

Image illustrant l’espacement entre les rangées 1 et 2 dans un plan structurel.

Détail d’espacement des rangées 1 et 2

Résumé du calcul de la résistance :

Paramètre	Unité	Semelle du poteau en flexion	Ame du poteau en traction transversale	Platine d’about en flexion
m	[mm]	33,4	-	-
ℓ_eff,1	[mm]	332	-	-
ℓ_eff,2	[mm]	332	-	-

MODE 1
n	[mm]	41.8	-	-
t_f	[mm]	20.5	-	-
f_y	[N/mm²]	265	-	-
M_pl,1,Rd	[Nmm]	9.24x10³	-	-
e_w	[mm]	9.9	-	-
F_T,1,Rd	[kN]	1420	-	-

MODE 2
M_pl,2,Rd	[Nmm]	9.24x10⁶	-	-
F_t,Rd	[N]	203	-	-
Boulons	[pcs]	4	-	-
∑F_t,Rd	[N]	812	-	-
F_T,2,Rd	[kN]	697	-	-

MODE 3
F_T,3,Rd	[kN]	812	-	-

ω	[-]	-	1.0	-
b_eff,t,wc	[mm]	-	332	-
t_wb	[mm]	-	12.8	-
f_y,wc	[N/mm²]	-	265	-

RÉSISTANCE		F_t,fc,Rd	F_t,wc,Rd	F_t,ep,Rd
	[kN]	697	1126	-
NOTE				Il n’y a pas de mode de groupe pour la platine d’about

La résistance des rangées de boulons 1 et 2 est la valeur minimale des résistances de la Semelle du poteau en flexion et Ame du poteau en traction, soit F_t,1-2,Rd = min {F_t,fc,Rd = 697; F_t,wc,Rd = 1126} = 697 kN.
La résistance de la rangée de boulons 2 du côté du poteau est donc limitée à F_t2,c,Rd = F_t,1-2,Rd - F_t1,Rd = 697 - 377 = 320 kN.

La résistance de la rangée de boulons 2 est la valeur minimale des résistances : Semelle du poteau en flexion F_t,fc,Rd = 398 kN, Ame du poteau en traction F_t,wc,Rd = 790 kN, Ame de la poutre en traction F_t,wb,Rd = 675 kN, Platine d’about en flexion F_t,ep,Rd = 406 kN et du côté du poteau, en tant que partie du groupe, F_t2,c,Rd = 320 kN. Par conséquent, la résistance de la rangée de boulons 2 F_t,2,Rd = 320 kN.

RANGÉE DE BOULONS 3
Tout d’abord, considérez la rangée 3 seule.

Résumé du calcul de la résistance :

Paramètre	Unité	Semelle du poteau en flexion	Ame du poteau en traction transversale	Platine d’about en flexion	Ame de la poutre en traction
e	[mm]	-	-	= e_p = 75	-
m	[mm]	-	-	38.6	-
ℓ_eff,1	[mm]	-	-	248	-
ℓ_eff,2	[mm]	-	-	248	-

MODE 1
n	[mm]	-	-	48.3	-
t_f	[mm]	-	-	25	-
f_y	[N/mm²]	-	-	265	-
M_pl,1,Rd	[Nmm]	-	-	10.1x10⁶	-
e_w	[mm]	-	-	9.9	-
F_T,1,Rd	[kN]	-	-	1291	-

MODE 2
M_pl,2,Rd	[Nmm]	-	-	10.3x10⁶	-
F_t,Rd	[N]	-	-	203	-
Boulons	[pcs]	-	-	2	-
∑F_t,Rd	[N]	-	-	406	-
F_T,2,Rd	[kN]	-	-	463	-

MODE 3
F_T,3,Rd	[kN]	-	-	406	-

b_eff,t,wb	[mm]	-	-	-	= b_eff,1 = 243
t_wb	[mm]	-	-	-	10.1

RÉSISTANCE		F_t,fc,Rd	F_t,wc,Rd	F_t,ep,Rd	F_t,wb,Rd
	[kN]	790	790	406	675
NOTE	telle que calculée pour les rangées de boulons 1 et 2	telle que calculée pour les rangées de boulons 1 et 2

Les résistances pour les rangées 2 et 3 ci-dessus considèrent toutes la résistance de la rangée agissant seule. Cependant, du côté du poteau, la résistance peut être limitée par la résistance du groupe des rangées 1, 2, et 3, ou par le groupe des rangées 2 et 3. Du côté de la poutre, la résistance peut être limitée par le groupe des rangées 2 et 3. Ces résistances de groupe seront maintenant prises en compte.

BOULONS 1, 2 ET 3 COMBINÉS
Talon du poteau en flexion
Les motifs circulaires et non circulaires sont comme suit :

Lignes de rupture circulaires et non circulaires

Résumé du calcul de la résistance :

Paramètre	Unité	Semelle du poteau en flexion	Ame du poteau en traction transversale
ℓ_eff,1	[mm]	422	-
ℓ_eff,2	[mm]	422	-

MODE 1
m	[mm]	33.4	-
n	[mm]	41.8	-
e_w	[mm]	9.9	-
t_f	[mm]	20.5	-
f_y	[N/mm²]	265	-
M_pl,1,Rd	[Nmm]	11,7x10⁶	-
F_T,1,Rd	[kN]	1797	-

MODE 2
M_pl,2,Rd	[Nmm]	11.7x10⁶	-
F_t,Rd	[kN]	203	-
Boulons	[pcs]	6	-
∑F_t,Rd	[kN]	1218	-
F_T,2,Rd	[kN]	988	-

MODE 3
F_T,3,Rd	[kN]	1218	-

ω	[-]	-	1.0
b_eff,t,wc	[mm]	-	422
t_wc	[mm]	-	12.8

RÉSISTANCE		F_t,fc,Rd	F_t,wc,Rd
	[kN]	988	1431

La résistance des boulons des rangées 1, 2 et 3 combinées, du côté du poteau, est la valeur minimale entre semelle du poteau en flexion et ame de la colonne en traction, soit 988 kN.
Par conséquent, la résistance de la rangée de boulons 3 du côté du poteau est limitée à : F_t3,c,Rd = F_t1-3,Rd - F_t1-2,Rd = 988 - 697 = 291 kN.

RANGÉES 2 ET 3 COMBINÉES
Résumé du calcul de la résistance :

Paramètre	Unité	Côté poteau - semelle en flexion	Ame du poteau en traction transversale	Côté poutre - platine en flexion	Poutre en traction
m	[mm]	33.4	-	38.6	-
n	[mm]	41.8	-	48.3	-
e_w	-	-	9.9	-
ℓ_eff,1	[mm]	323	-	379	-
ℓ_eff,2	[mm]	323	-	379	-

MODE 1			(rangées 2 + 3)
M_pl,1,Rd	[Nmm]	9.24x10³	9.0x10⁶	15,7x10⁶	-
F_T,1,Rd	[kN]	1383	-	2007	-

MODE 2			(rangées 2 + 3)
M_pl,2,Rd	[Nmm]	9.0x10⁶	-	15,7x10⁶	-
F_t,Rd	[kN]	203	-	203	-
Boulons	[pcs]	4	-	4	-
∑F_t,Rd	[kN]	812	-	812	-
F_T,2,Rd	[kN]	691	-	813	-

MODE 3			(rangées 2 + 3)
F_T,3,Rd	[kN]	1218	-	812	-

ω	[-]	-	1.0	-	-
b_eff,t,wc	[mm]	-	323	-	-
t_wb	[mm]	-	12.8	-	-
f_y,wc	[N/mm²]	-	265	-	-

RÉSISTANCE		F_t,fc,Rd	F_t,wc,Rd	F_t,ep,Rd
	[kN]	691	1096	812	-
NOTE					n'est pas applicable

La résistance des boulons des rangées 2 et 3 combinées, du côté de la poutre, est Platine en flexion F_t,ep,Rd = 812 kN. Par conséquent, du côté de la poutre F_t2-3,Rd = 812 kN. La résistance de la rangée de boulons 3 du côté de la poutre est donc limitée à F_t3,b,Rd = F_t2-3,Rd - F_t2,Rd = 812 - 320 = 492 kN.

La résistance des boulons des rangées 2 et 3 combinées, du côté de la colonne, est semelle du poteau en flexion F_t,fc,Rd = 691 kN, âme du poteau en traction F_t,wc,Rd = 1096 kN, donc, du côté de la colonne F_t2-3,Rd = 691 kN.
Ainsi, la résistance de la rangée de boulons 3 du côté de la colonne est limitée à F_t3,b,Rd = F_t2-3,Rd - F_t2,Rd = 691 - 320 = 371 kN.

Résumé
La résistance de la rangée de boulons 3 est la valeur minimale parmi les résistances suivantes : semelle du poteau en flexion F_t,fc,Rd = 398 kN, âme de la colonne en traction F_t,wc,Rd = 790 kN, âme de la poutre en traction F_t,wb,Rd = 675 kN, platine en flexion F_t,ep,Rd = 406 kN, côté poteau en tant que partie d’un groupe avec 2 et 1 F_t3,c,Rd = 291 kN, côté poteau en tant que partie d’un groupe avec 2 F_t3,c,Rd = 371 kN, côté poutre en tant que partie d’un groupe avec 2 F_t3,b,Rd = 492 kN. Par conséquent, la résistance de la rangée de boulons 3 est F_t3,Rd = 291 kN.

RÉSUMÉ DES RÉSISTANCES EN TRACTION
La dérivation des résistances efficaces des rangées de traction ci-dessus peut être résumée sous forme tabulaire, comme montré ci-dessous.

Résistances des rangées F_tr,Rd :

	Semelle du poteau	Ame du poteau	Platine d’about	Ame de la poutre	Minimum	Résistance effective
Rangée 1, seule	398	790	377	N/A	377	377

Rangée 2, seule	398	790	406	675	398
Rangée 2, avec la rangée 1	697	1126	N/A	N/A	697
Rangée 2					697 - 377	320

Rangée 3, seule	398	790	406	675	309
Rangée 3, avec rangée 1 et 2	988	1431	N/A	N/A	988
Rangée 3					988 - 697	291
Rangée 3, avec la rangée 2	691	1096	812	1052	691
Rangée 3					691 - 320

Zone en compression

Ame du poteau en compression transversale
La résistance de calcul d’une âme de poteau non raidie en compression transversale est déterminée comme suit :

\begin{array}{l} Résistance à l’écrasement : \\ F_{c, w c, R d} = \begin{array}{c} ω k_{w c} b_{e f f, c, w c} t_{w c} f_{y, w c,} \\ γ_{M 0} \end{array}, \\ \begin{array}{l} mais (résistance au flambement) : \\ F_{c, w c, R d} \leq \begin{array}{c} ω k_{w c} ρ b_{e f f, c, w c} t_{w c} f_{y, w c .} \\ γ_{mod ulus of rigidity, θi Peq0)1} \end{array} . \end{array} \end{array}

Âme de poteau en compression transversale

où
s	= r_c = 12,7 mm pour les sections de poteau laminées I et H
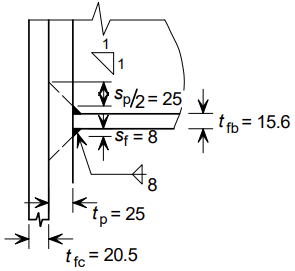
s_p	est la longueur obtenue par dispersion à 45° à travers la platine d’about; s_p = 2 t_p = 50 mm
e_x	est la distance d’about mesurée depuis le centre de fixation de la rangée 1; e_x = 50 mm
x	est l’espacement de la rangée 1 au-dessus de la semelle de la poutre mesuré depuis le centre de fixation; x = 40 mm
s_f	est la hauteur du cordon de soudure ; s_f = 8 mm
h_p	est la profondeur de la platine d’about ; h_p ≥ e_x + x + h_b + s_f + t_p = 656 mm → h_p = 670 mm
b_eff,c,wc	pour une platine d’about boulonnée; b_eff,c,wc = t_fb + 2 s_f + 5 (t_fc + s) + s_p = 248 mm
ρ	est le facteur de réduction pour le flambement des plaques, il dépend de la plaque; ρ = 1.0
ω	= 1.0
k_wc	est un facteur de réduction qui tient compte de la compression dans l’âme du poteau ; k_wc = 1.0

Dimensions précises des plats d’about boulonnés décrites dans le dessin technique | Détails d’ingénierie

Dimensions de la plaque d’about boulonnée

Par conséquent, F_c,wc,Rd = 841 kN.

Semelle et âme de la poutre en compression
La résistance de calcul résultante d’une semelle de poutre et de la zone en compression adjacente de l’âme est déterminée en utilisant :

F_{c, f b, R d} = \begin{matrix} M_{c, R d} \\ h - t_{f b} \end{matrix}

Résistance de calcul de la semelle de poutre et de l'âme en compression

où
M_c,Rd	est la résistance de calcul de la poutre ; en supposant que l’effort tranchant de calcul dans la poutre ne réduit pas M_c,Rd, donc, M_c,Rd = 649 kN
h	= h_b = 533,1 mm
t_fb	= 15,6 mm

Ainsi, F_c,fb,Rd = 1254 kN.

Résumé : résistance de la zone en compression
Ame du poteau en compression transversale F_c,wc,Rd = 841 kN, Semelle et âme de la poutre en compression F_c,fb,Rd = 1254 kN.

Résistance du panneau d’âme de la colonne en cisaillement
La résistance au cisaillement plastique d'une âme non raidie est donnée par :

V_{w p, R d} = \begin{matrix} 0.9 f_{y, w c} A_{v c} \\ \sqrt{3} γ_{M 0} \end{matrix}

Résistance au cisaillement du panneau d'âme du poteau

La résistance n’est pas évaluée ici, car il n’y a pas de cisaillement de calcul dans l'âme, les moments des poutres étant égaux et opposés.

Résistance au Moment

RÉSISTANCE EFFECTIVE DES RANGÉES DE BOULONS

Distribution de force | Analyse de résistance au moment

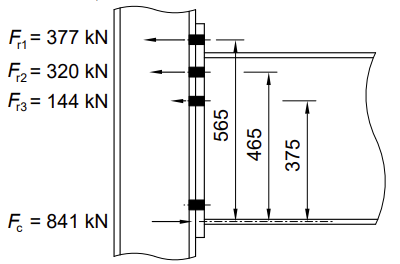
Les résistances effectives de chacune des trois rangées de boulons dans la zone de traction sont :
F_t1,Rd = 377 kN, F_t2,Rd = 320 kN, F_t3,Rd = 291 kN.

Les résistances effectives doivent être réduites si la résistance de l'une des rangées supérieures dépasse 1,9 F_t,Rd = 1,9 x 203 = 386 kN.
Ainsi, aucune réduction n’est requise.

ÉQUILIBRE DES FORCES
La somme des efforts de traction, ainsi que toute compression axiale dans la poutre, ne peut pas dépasser la résistance de la zone en compression.
De même, le cisaillement de calcul ne peut pas dépasser la résistance au cisaillement du panneau d’âme du poteau. Cela n’est pas pertinent dans cet exemple, les moments dans les poutres identiques étant égaux et opposés.

Pour l’équilibre horizontal ∑F_tr,Rd + N_Ed = F_c,Rd. Dans cet exemple, il n’y a pas de compression axiale. Ainsi, ∑F_tr,Rd = F_c,Rd.

Ici, la résistance totale en traction effective ∑F_tr,Rd = 377 + 320 + 291 = 988 kN qui dépasse la résistance en compression F_с,Rd = 841 kN.
Pour atteindre l’équilibre, les résistances effectives sont réduites, en commençant par la rangée la plus basse et en remontant, jusqu’à atteindre l’équilibre. La réduction requise est de 988 - 841 = 147 kN.
Toute cette réduction peut être réalisée en réduisant la résistance de la rangée inférieure. Ainsi, F_t3,Rd = 291 - 147 = 144 kN.

Diagram d’équilibre des forces montrant les vecteurs de charge équilibrés | analyse en génie civil

Analyse du diagramme d’équilibre des forces

RÉSISTANCE AU MOMENT DES FORCES
La résistance au moment de l’assemblage poutre-poteau M_j,Rd :

M_{j, R d} = \sum h_{r} F_{t r, R d}

Résistance à la flexion de l’assemblage poutre-poteau

En prenant le centre de la compression comme le milieu de l’épaisseur de la semelle en compression de la poutre, h_r1 = 565 mm, h_r2 = 465 mm, h_r3 = 375 mm. Ainsi, la résistance au moment de l’assemblage poutre-poteau est de :

M_j,Rd = 416 kNm.

Résistance au cisaillement vertical

RÉSISTANCE DU GROUPE DE BOULONS
La résistance au cisaillement d’un boulon M24 de classe 8.8 non précontraint en cisaillement simple est F_v,Rd = 136 kN, F_b,Rd = 200 kN (pour une tôle de 20 mm). Ainsi, F_v,Rd prédomine.

La résistance au cisaillement des rangées supérieures peut être prise de manière conservatrice comme étant 28% de la résistance au cisaillement sans traction (en supposant que ces boulons sont pleinement utilisés en traction). Ainsi, la résistance au cisaillement de toutes les 4 rangées est (2 + 6 x 0.28) 136 = 3.68 x 136 = 500 kN.

Vérification de soudure

L’approche simple exige que les soudures à la semelle en traction et à l’âme soient de pleine résistance, tandis que la soudure à la semelle en compression soit de taille nominale uniquement, en supposant qu’elle a été préparée avec une extrémité coupée à la scie.

SOUDURES DE LA SEMELLE EN TRACTION DE LA POUTRE
Une soudure de pleine résistance est fournie par des soudures d’angle symétriques avec une épaisseur totale de gorge au moins égale à l’épaisseur de la semelle. La taille de gorge requise est t_fb/2 = 15.6/2 = 7.8 mm. La gorge de soudure prévue est a_f = 12/√2 = 8.5 mm, ce qui est adéquat.

SOUDURES DE LA SEMELLE EN COMPRESSION DE LA POUTRE
Fournir une soudure d'angle nominale de chaque côté de la semelle de la poutre. Une soudure d'angle de 8 mm de hauteur de cordon sera satisfaisante.

SOUDURES DE L’AME DE LA POUTRE
Pour plus de commodité, une soudure de pleine résistance est fournie à l'âme.
La taille de gorge requise est t_fw/2 = 10.2/2 = 5.1 mm.
La gorge de soudure fournie est a_p = 8/√2 = 5.7 mm, ce qui est adéquat.

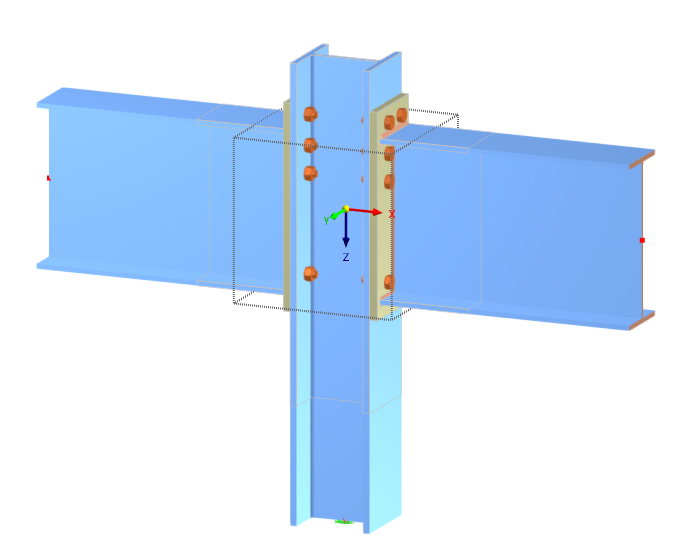
ANALYSE PAR ÉLÉMENTS FINIS BASÉE SUR LES COMPOSANTS

La vérification a été réalisée à l’aide du module complémentaire Assemblages acier pour RFEM 6.
Le module complémentaire Assemblages acier permet l'analyse d’assemblages sur la base d’un modèle EF. L'entrée et l'évaluation des résultats sont entièrement intégrées à l'interface utilisateur du logiciel RFEM, rendant le processus de vérification intuitif et rapide.

Configuration de l’assemblage

L'assemblage en acier est illustré avec des détails clairs de connexion entre les barres en acier.

Aperçu de l’assemblage acier | Détail de connexion

Colonne	254x254x107 UKC	S275
Poutre	section paramétriquement définie
	h_b = 533.1 mm, b_b = 209.3 mm, t_wb = 10.1 mm, t_fb = 15.6 mm	S275
Platine d’about	670x250x25 mm	S275
Boulon	M24 classe 8.8
Soudures	Soudures d'angle de la semelle supérieure s_f1 = 8.5 mm, semelle inférieure s_f2 = 5.7 mm, âme s_w = 5.7 mm

Résultats du module complémentaire Assemblages acier

Le module complémentaire Assemblages acier pour RFEM 6 améliore les capacités du logiciel en permettant aux ingénieurs d'analyser des assemblages en acier avec la précision d'un modèle par éléments finis (EF). Cet outil avancé permet une visualisation détaillée de tous les résultats essentiels directement sur le modèle EF, fournissant un aperçu clair et complet de la performance des assemblages en acier sous diverses charges et conditions.

Il inclut l'affichage des contraintes équivalentes et des déformations plastiques au sein de l’assemblage en acier. En montrant à la fois les contraintes équivalentes et les déformations plastiques, RFEM offre une compréhension plus complète du comportement de l’assemblage dans des conditions réelles, ce qui assure un calcul à la fois sûr et efficace.

CONTRAINTES ÉQUIVALENTES
Les contraintes équivalentes fournissent une vue claire de la distribution globale des contraintes, aidant les ingénieurs à identifier les points de défaillance potentiels causés par des concentrations de contrainte excessives. Ces contraintes sont essentielles pour comprendre la capacité de charge de l’assemblage.

Représentation visuelle des contraintes équivalentes sur une assemblage, illustrant la répartition des contraintes et les zones potentielles de concentration des contraintes.

Contraintes équivalentes affichées sur la géométrie de l’assemblage

Ici, la distribution des contraintes sur le talon de la colonne et la platine d’about de la poutre peut être vue.

Représentation visuelle de la répartition des contraintes équivalentes sur un platine d’about, montrant des variations de contraintes en code couleur.

Contraintes équivalentes affichées sur le faux-plateau

Représentation visuelle de la distribution des contraintes équivalentes sur un fer de colonne illustrant les variations de contraintes.

Contraintes équivalentes affichées sur le voile du poteau

DÉFORMATION PLASTIQUE
Les plaques dans l’assemblage sont vérifiées plastiquement en comparant la déformation plastique existante à la déformation plastique admissible. Le réglage par défaut est de 5 %, selon EN 1993‑1‑5, Annexe C. Ci-dessous, la déformation plastique dans l’assemblage :

L'image affiche la distribution de la déformation plastique sur une structure d'assemblage avec des dégradés de couleur indiquant l'intensité de la déformation.

Déformation plastique indiquée sur la géométrie de l’assemblage

ANALYSE CONTRAINTE-DÉFORMATION

Analyse de la distribution des contraintes et des déformations sur les plaques structurelles, montrant les résultats de vérification de la conception pour garantir la conformité aux normes.

Analyse contrainte-déformation, Vérification de plaques

Illustration des résultats de l’analyse contrainte-déformation et des vérifications de conception de soudure, montrant les capacités portantes des assemblages structurels.

Analyse contrainte-déformation, Vérification de soudure

Analyse technique de la conception de fixations et de connecteurs dans un élément structurel à l’aide d’un logiciel spécialisé.

Vérification pour fixations

Conclusions

L'article présente deux méthodes pour vérifier des assemblage poutre-poteau. La méthode analytique est complexe et difficile à gérer manuellement, en particulier en ce qui concerne l’optimisation. Elle implique le calcul des résistances de chaque composant et leur comparaison avec les forces agissant sur ces composants.

La deuxième méthode est l'approche CBFEM, mise en œuvre dans le module complémentaire Assemblages acier pour RFEM 6. Avec cette méthode, l’assemblage est assemblé et les forces pour l'analyse sont dérivées du modèle EF principal. L’assemblage est ensuite vérifié sous les forces appliquées grâce à l'analyse contrainte-déformation des plaques en acier. De plus, la vérification des soudures et des organes d’assemblage est réalisée selon les normes EN pertinentes.

Bien que la méthode analytique soit largement utilisée, la deuxième méthode est beaucoup plus rapide, fournissant des résultats précis tout en réduisant considérablement le temps de calcul. Elle permet également une optimisation facile et rapide.

Ci-dessous, une comparaison des résultats.
La résistance au moment M_j,Rd calculée à l'aide de l'approche analytique est de 416 kNm, tandis que la valeur de la méthode CBFEM dans le module complémentaire Assemblages acier est de 415 kNm. La différence est inférieure à 1 %, avec Δ = -0,24 %, illustrant la fiabilité et la précision de la méthode CBFEM mise en œuvre dans le module complémentaire Assemblages acier.

Le modèle est disponible ci-dessous :

Modèle 005595 | L’image montre une connexion par platine d’about boulonnée non raidie utilisée dans des assemblages en acier structurel.

310x

86x

Assemblage par boulons avec plaque d'about sans raidisseur

RÉFÉRENCES

[1] Brown, D., Iles, D., Brettle, M., Malik, A., et BCSA/SCI Connections Group. (2013). Assemblages dans les constructions en acier : Assemblages résistants au moment selon l’Eurocode 3. Vol BCSA/SCI Connections Group. Londres : The British Constructional Steelwork Association Limited.

;