624x

001938

2025-04-01

Unstiffened Bolted End Plate Connection

This article examines the unstiffened bolted end plate connection, a common structural steel connection used in construction. Analytical calculations based on Eurocode 3 guidelines are compared with results obtained from the Steel Joints add-on in RFEM 6. The focus is on assessing the accuracy and reliability of the CBFEM method in capturing structural behavior and load responses in steel structures. This study aims to deepen the understanding of how well FEM software performs, providing practical insights for professionals in structural engineering.

INTRODUCTION

This article provides guidance on designing moment-resisting joints in accordance with Eurocode 3, specifically targeting bolted end plate connections between beams and columns in multi-story frames. It references relevant sections, figures, and tables from EN 1993-1-8 and other applicable standards as needed.

ANALYTICAL APPROACH

The analytical procedure is taken from [1].

Joint Configuration

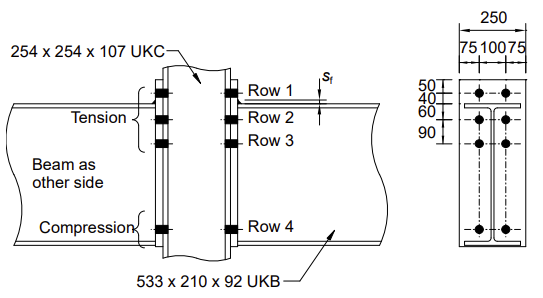
Illustration of a steel bolted joint with precise dimensions and configuration details.

Steel Connection Design Diagram

Column	254x254x107 UKC	S275
Beam	533x210x92 UKB	S275
End plate	670x250x25 mm	S275
Bolt	M24 class 8.8
Welds	Fillet welds: flange s_f = 12 mm, web s_w = 8 mm

Equivalent T-Stub Resistance

The resistance of the equivalent T-stubs is evaluated separately for the end plate and the column flange. The resistances are calculated for three possible modes of failure, and the resistance is taken as the minimum of the values for these three modes.

The design resistance of the T-stub flange for each of the modes is given below.

A technical interface displaying simulation results for steel joint failure modes with color-coded stress zones.

Failure Modes in Steel Joints: An Add-on Assessment

The modes of failure are shown below:

\begin{array}{l} Mode 1. Complete Flange Yielding \\ F_{T, 1, R d} = \begin{matrix} (8 n - 2 e_{w}) M_{p l, 1, R d} \\ 2 m n - e_{w} (m + n) \end{matrix} \\ \begin{array}{l} Mode 2. Bolt Failure with Flange Yielding \\ F_{T, 2, R d} = \begin{array}{c} 2 M_{p l, 2, R d} + n (\sum F_{t, R d}) \\ m + n \end{array} \\ \begin{array}{l} Mode 3. Bolt Failure \\ F_{T, 3, R d} = \sum F_{t, R d} \end{array} \end{array} \end{array}

Modes of Failure

\begin{matrix} \begin{matrix} M_{p l, 1, R d} = \begin{array}{c} 0.25 \sum l_{e f f, 1} t_{f}^{2} f_{y} \\ γ_{M 0} \end{array}, \\ M_{p l, 2, R d} = \begin{array}{c} 0.25 \sum l_{e f f, 2} t_{f}^{2} f_{y} \\ γ_{M 0} \end{array} . \end{matrix} \end{matrix}

Plastic Resistance Moments of Equivalent T-Stub for Modes 1 and 2

where
ℓ_eff,1	is the effective length of the equivalent T-stub for Mode 1, taken as the lesser of ℓ_eff,cp and ℓ_eff,nc
ℓ_eff,2	is the effective length of the equivalent T-stub for Mode 2, taken as ℓ_eff,nc
t_f	in the thickness of T-stub flange (= t_p or t_fc)
f_y	is the yield strength of the T-stub flange (i.e. of the column or end plate)
∑F_t,Rd	is the total tension resistance for the bolts in the T-stub (= 2F_t,Rd for a single row)
e_w	= d_w/4
d_w	is the diameter of the washer or the width across the points of the bolt head
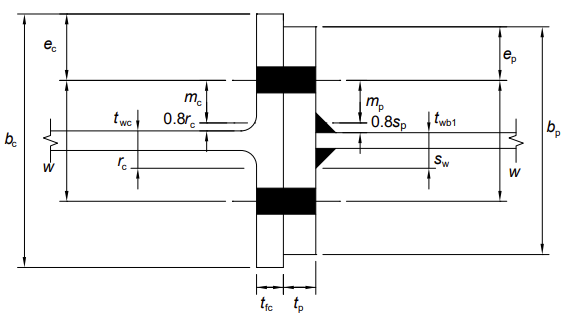
m	is the distance as defined in the figure above
n	is the minimum of e_c (the edge distance of the column flange), e_p (the edge distance of the end plate), 1.25 m (for the end plate or the column flange, as appropriate)

Resistance definition:

\begin{array}{l} Resistance of column flange in bending \\ F_{t, f c, R d} = \min {F_{T, 1, R d}, F_{T, 2, R d}, F_{T, 3, R d}} \\ \begin{array}{l} Resistance of an unstiffened column web to transverse tension \\ F_{t, w c, R d} = \begin{array}{c} ω b_{e f f, t, w c} t_{w c} f_{y, w c} \\ γ_{M 0} \end{array} \\ Resistance of the end plate in bending \\ F_{t, e p, R d} = \min {F_{T, 1, R d}, F_{T, 2, R d}, F_{T, 3, R d}} \\ \begin{matrix} \begin{array}{l} Resistance of the beam web \\ F_{t, w b, R d} = \begin{array}{c} b_{e f f, t, w b} t_{w b} f_{y, b} \\ γ_{M 0} \end{array} \end{array} \end{matrix} \end{array} \end{array}

Resistance of Column Flange in Bending

Tension Zone T-Stubs

BOLT ROW 1
Column flange in bending (no backing plate)
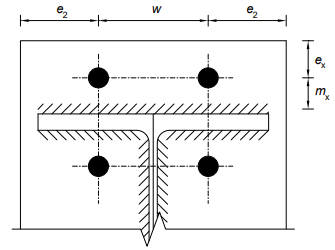
Consider bolt row 1 acting alone. The key dimensions are shown below.

Steel connection detail illustrating a tension zone T-stub component in a precise steel joint

Tension Zone T-stub Joint Detail

End plate in bending

Key dimensions for the T-stub row1 and steel joints add-on in RFEM 6

T-stub Key Dimensions Overview

Summary of resistance computation:

Parameter	Unit	Column flange in bending (no backing plate)	Column web in transverse tension	End plate in bending	Beam web in tension
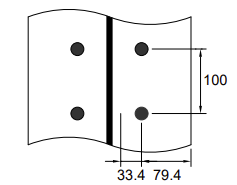
m	[mm]	33.4	-	= m_x = 30.4	-
e	[mm]	= e_min = 75	-	e = 75, e_x = 50	-
ℓ_eff,1	[mm]	210	-	125	-
ℓ_eff,2	[mm]	233	-	125	-

MODE 1
n	[mm]	41.8	-	38.0	-
t_f	[mm]	20.5	-	25	-
f_y	[N/mm²]	265	-	265	-
M_pl,1,Rd	[Nmm]	5850x10³	-	5180x10³	-
d_w	[mm]	39.55	-	-	-
e_w	[mm]	9.9	-	9.9	-
F_T,1,Rd	[kN]	898	-	901	-

MODE 2
M_pl,2,Rd	[Nmm]	6490x10³	-	5180x10³	-
F_t,Rd	[N]	203x10³	-	203x10³	-
Bolt in a row	[pcs]	2	-	2	-
∑F_t,Rd	[N]	406x10³	-	406x10³	-
F_T,2,Rd	[kN]	398	-	377	-

MODE 3
F_T,3,Rd	[kN]	406	-	406	-

ω	[-]	-	1.0	-
b_eff,t,wc	[mm]	-	= ℓ_eff,2 = 233	-
f_y,wc	[N/mm²]	-	= f_y,c = 265	-

RESISTANCE		F_t,fc,Rd	F_t,wc,Rd	F_t,ep,Rd
	[kN]	398	790	377
NOTE					is not applicable

The resistance of bolt row 1 is the smallest value of the resistances mentioned above.
Therefore, F_t,1,Rd = min {F_t,fc,Rd = 398; F_t,wc,Rd = 790; F_t,ep,Rd = 377} = 377 kN.

BOLT ROW 2
Firstly, consider row 2 alone.

End plate in bending
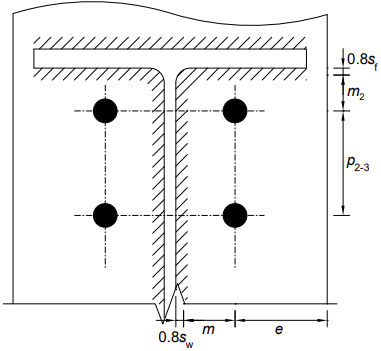
Bolt row 2 is the first bolt row below the beam flange, considered as the 'first bolt row below the tension flange of the beam'. The key dimensions for the T-stub are shown for the column flange T-stub in row 1 and as shown below (in elevation) for row 2.

Diagram showing key T-stub dimensions in row 2 for steel joint analysis.

T-Stub Dimensions Row 2

Summary of resistance computation:

Parameter	Unit	Column flange in bending	Column web in transverse tension	End plate in bending	Beam web in tension
m	[mm]	-	-	= m_p = 38.6	-
m₂	[mm]	-	-	34.8	-
e	[mm]	-	-	= e_p = 75	-
ℓ_eff,1	[mm]	-	-	243	-
ℓ_eff,2	[mm]	-	-	290	-

MODE 1
n	[mm]	-	-	48.3	-
t_f	[mm]	-	-	25	-
f_y	[N/mm²]	-	-	265	-
M_pl,1,Rd	[Nmm]	-	-	10.1x10³	-
e_w	[mm]	-	-	9.9	-
F_T,1,Rd	[kN]	-	-	1291	-

MODE 2
M_pl,2,Rd	[Nmm]	-	-	12.0x10⁶	-
F_t,Rd	[N]	-	-	203x10³	-
Bolt in a row	[pcs]	-	-	2	-
∑F_t,Rd	[N]	-	-	406x10³	-
F_T,2,Rd	[kN]	-	-	502	-

MODE 3
F_T,3,Rd	[kN]	-	-	406	-

ω	[-]	-	-	-	1.0
b_eff,t,wc	[mm]	-	-	-	243
t_wb	[mm]	-	-	-	10.1
f_y,wc	[N/mm²]	-	-	-	675

RESISTANCE		F_t,fc,Rd	F_t,wc,Rd	F_t,ep,Rd	F_t,wb,Rd
	[kN]	398	790	406	675
NOTE		as calculated for bolt row 1, Mode 2	as calculated for bolt row 1

The resistances for row 2 above all consider the row acting alone. However, on the column side, the resistance may be limited by the resistance of the group of rows 1 and 2. The group resistance is now considered.

ROWS 1 AND 2 COMBINED
Column flange in bending

Image depicting the spacing relationship between row 1 and row 2 in a structural layout.

Row 1 and 2 Spacing Detail

Summary of resistance computation:

Parameter	Unit	Column flange in bending	Column web in transverse tension	End plate in bending
m	[mm]	33.4	-	-
ℓ_eff,1	[mm]	332	-	-
ℓ_eff,2	[mm]	332	-	-

MODE 1
n	[mm]	41.8	-	-
t_f	[mm]	20.5	-	-
f_y	[N/mm²]	265	-	-
M_pl,1,Rd	[Nmm]	9.24x10³	-	-
e_w	[mm]	9.9	-	-
F_T,1,Rd	[kN]	1420	-	-

MODE 2
M_pl,2,Rd	[Nmm]	9.24x10⁶	-	-
F_t,Rd	[N]	203	-	-
Bolts	[pcs]	4	-	-
∑F_t,Rd	[N]	812	-	-
F_T,2,Rd	[kN]	697	-	-

MODE 3
F_T,3,Rd	[kN]	812	-	-

ω	[-]	-	1.0	-
b_eff,t,wc	[mm]	-	332	-
t_wb	[mm]	-	12.8	-
f_y,wc	[N/mm²]	-	265	-

RESISTANCE		F_t,fc,Rd	F_t,wc,Rd	F_t,ep,Rd
	[kN]	697	1126	-
NOTE				There is no group mode for the end plate

Resistance of bolt rows 1 and 2 is the smallest value of resistances Column flange in bending and Column web in tension, that is F_t,1-2,Rd = min {F_t,fc,Rd = 697; F_t,wc,Rd = 1126} = 697 kN.
The resistance of bolt row 2 on the Column side is therefore limited to F_t2,c,Rd = F_t,1-2,Rd - F_t1,Rd = 697 - 377 = 320 kN.

Resistance of bolt row 2 is the smallest value of resistances: Column flange in bending F_t,fc,Rd = 398 kN, Column web in tension F_t,wc,Rd = 790 kN, Beam web in tension F_t,wb,Rd = 675 kN, End plate in bending F_t,ep,Rd = 406 kN and Column side, as a part of the group, F_t2,c,Rd = 320 kN. Therefore, the resistance of the bolt row 2 F_t,2,Rd = 320 kN.

BOLT ROW 3
Firstly, consider row 3 alone.

Summary of resistance computation:

Parameter	Unit	Column flange in bending	Column web in transverse tension	End plate in bending	Beam web in tension
e	[mm]	-	-	= e_p = 75	-
m	[mm]	-	-	38.6	-
ℓ_eff,1	[mm]	-	-	248	-
ℓ_eff,2	[mm]	-	-	248	-

MODE 1
n	[mm]	-	-	48.3	-
t_f	[mm]	-	-	25	-
f_y	[N/mm²]	-	-	265	-
M_pl,1,Rd	[Nmm]	-	-	10.1x10⁶	-
e_w	[mm]	-	-	9.9	-
F_T,1,Rd	[kN]	-	-	1291	-

MODE 2
M_pl,2,Rd	[Nmm]	-	-	10.3x10⁶	-
F_t,Rd	[N]	-	-	203	-
Bolts	[pcs]	-	-	2	-
∑F_t,Rd	[N]	-	-	406	-
F_T,2,Rd	[kN]	-	-	463	-

MODE 3
F_T,3,Rd	[kN]	-	-	406	-

b_eff,t,wb	[mm]	-	-	-	= b_eff,1 = 243
t_wb	[mm]	-	-	-	10.1

RESISTANCE		F_t,fc,Rd	F_t,wc,Rd	F_t,ep,Rd	F_t,wb,Rd
	[kN]	790	790	406	675
NOTE	as calculated for bolt rows 1 and 2	as calculated for bolt rows 1 and 2

The resistances for rows 2 and 3 above all consider the resistance of the row acting alone. However, on the column side, the resistance may be limited by the resistance of the group of rows 1, 2, and 3, or by the group of rows 2 and 3. On the beam side, the resistance may be limited by the group of rows 2 and 3. These group resistances are now considered.

BOLTS 1, 2 AND 3 COMBINED
Column flange in bending
The circular and non-circular patterns are as follows:

Circular and Non-Circular Yield Line Patterns

Summary of resistance computation:

Parameter	Unit	Column flange in bending	Column web in transverse tension
ℓ_eff,1	[mm]	422	-
ℓ_eff,2	[mm]	422	-

MODE 1
m	[mm]	33.4	-
n	[mm]	41.8	-
e_w	[mm]	9.9	-
t_f	[mm]	20.5	-
f_y	[N/mm²]	265	-
M_pl,1,Rd	[Nmm]	11.7x10⁶	-
F_T,1,Rd	[kN]	1797	-

MODE 2
M_pl,2,Rd	[Nmm]	11.7x10⁶	-
F_t,Rd	[kN]	203	-
Bolts	[pcs]	6	-
∑F_t,Rd	[kN]	1218	-
F_T,2,Rd	[kN]	988	-

MODE 3
F_T,3,Rd	[kN]	1218	-

ω	[-]	-	1.0
b_eff,t,wc	[mm]	-	422
t_wc	[mm]	-	12.8

RESISTANCE		F_t,fc,Rd	F_t,wc,Rd
	[kN]	988	1431

Resistance of bolt rows 1, 2 and 3 combined, on the column side, is the smallest value of Column flange in bending and Column web in tension, that is 988 kN.
Therefore, the resistance of bolt row 3 on the column side is limited to: F_t3,c,Rd = F_t1-3,Rd - F_t1-2,Rd = 988 - 697 = 291 kN.

ROWS 2 AND 3 COMBINED
Summary of resistance computation:

Parameter	Unit	Column side - flange in bending	Column web in transverse tension	Beam side - end plate in bending	Beam in tension
m	[mm]	33.4	-	38.6	-
n	[mm]	41.8	-	48.3	-
e_w	-	-	9.9	-
ℓ_eff,1	[mm]	323	-	379	-
ℓ_eff,2	[mm]	323	-	379	-

MODE 1			(rows 2 + 3)
M_pl,1,Rd	[Nmm]	9.24x10³	9.0x10⁶	15.7x10⁶	-
F_T,1,Rd	[kN]	1383	-	2007	-

MODE 2			(rows 2 + 3)
M_pl,2,Rd	[Nmm]	9.0x10⁶	-	15.7x10⁶	-
F_t,Rd	[kN]	203	-	203	-
Bolts	[pcs]	4	-	4	-
∑F_t,Rd	[kN]	812	-	812	-
F_T,2,Rd	[kN]	691	-	813	-

MODE 3			(rows 2 + 3)
F_T,3,Rd	[kN]	1218	-	812	-

ω	[-]	-	1.0	-	-
b_eff,t,wc	[mm]	-	323	-	-
t_wb	[mm]	-	12.8	-	-
f_y,wc	[N/mm²]	-	265	-	-

RESISTANCE		F_t,fc,Rd	F_t,wc,Rd	F_t,ep,Rd
	[kN]	691	1096	812	-
NOTE					is not applicable

Resistance of bolt rows 2 and 3 combined, on the beam side, is End plate in bending F_t,ep,Rd = 812 kN. Therefore, on the beam side F_t2-3,Rd = 812 kN. The resistance of bolt row 3 on the beam side is therefore limited to F_t3,b,Rd = F_t2-3,Rd - F_t2,Rd = 812 - 320 = 492 kN.

Resistance of the bolt rows 2 and 3 combined, on the column side, is Column flange in bending F_t,fc,Rd = 691 kN, Column web in tension F_t,wc,Rd = 1096 kN, therefore, on the column side F_t2-3,Rd = 691 kN.
Hence, the resistance of bolt row 3 on the column side is limited to F_t3,b,Rd = F_t2-3,Rd - F_t2,Rd = 691 - 320 = 371 kN.

Summary
The resistance of bolt row 3 is the smallest value among the following resistances: Column flange in bending F_t,fc,Rd = 398 kN, Column web in tension F_t,wc,Rd = 790 kN, Beam web in tension F_t,wb,Rd = 675 kN, End plate in bending F_t,ep,Rd = 406 kN, Column side as part of a group with 2 and 1 F_t3,c,Rd = 291 kN, Column side as part of a group with 2 F_t3,c,Rd = 371 kN, Beam side as part of a group with 2 F_t3,b,Rd = 492 kN. Therefore, the resistance of the bolt row 3 is F_t3,Rd = 291 kN.

SUMMARY OF TENSION RESISTANCES
The derivation of the effective resistances of the tension rows above can be summarized in tabular form, as shown below.

Resistances of rows F_tr,Rd:

	Column flange	Column web	End plate	Beam web	Minimum	Effective resistance
Row 1, alone	398	790	377	N/A	377	377

Row 2, alone	398	790	406	675	398
Row 2, with row 1	697	1126	N/A	N/A	697
Row 2					697 - 377	320

Row 3, alone	398	790	406	675	309
Row 3, with row 1 and 2	988	1431	N/A	N/A	988
Row 3					988 - 697	291
Row 3, with row 2	691	1096	812	1052	691
Row 3					691 - 320

Compression Zone

Column web in transverse compression
The design resistance of an unstiffened column web in transverse compression is determined as follows:

\begin{array}{l} Crushing resistance: \\ F_{c, w c, R d} = \begin{array}{c} ω k_{w c} b_{e f f, c, w c} t_{w c} f_{y, w c} \\ γ_{M 0} \end{array}, \\ \begin{array}{l} but (buckling resistance): \\ F_{c, w c, R d} \leq \begin{array}{c} ω k_{w c} ρ b_{e f f, c, w c} t_{w c} f_{y, w c} \\ γ_{M 1} \end{array} . \end{array} \end{array}

Column Web in Transverse Compression

where
s	= r_c = 12.7 mm for hot rolled I and H column sections
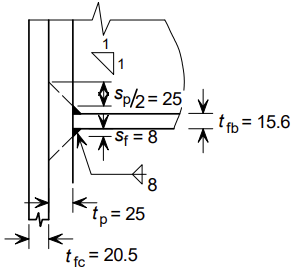
s_p	is the length obtained by dispersion at 45° through the end plate; s_p = 2 t_p = 50 mm
e_x	is the end distance measured from the row 1 fastener centre; e_x = 50 mm
x	is the spacing row 1 above the the beam flange measured from the fastener centre; x = 40 mm
s_f	is the weld leg size; s_f = 8 mm
h_p	is the depth of the end plate; h_p ≥ e_x + x + h_b + s_f + t_p = 656 mm → h_p = 670 mm
b_eff,c,wc	for a bolted end plate; b_eff,c,wc = t_fb + 2 s_f + 5 (t_fc + s) + s_p = 248 mm
ρ	is the reduction factor for plate buckling, it depends on the plate; ρ = 1.0
ω	= 1.0
k_wc	is a reduction factor that accounts for compression in the column web; k_wc = 1.0

Precise bolted end plate dimensions outlined in technical drawing | Engineering details

Bolted End Plate Dimensions | Engineering Detail Documentation

Therefore, F_c,wc,Rd = 841 kN.

Beam flange and web in compression
The resultant design resistance of a beam flange and the adjacent compression zone of the web is determined using:

F_{c, f b, R d} = \begin{matrix} M_{c, R d} \\ h - t_{f b} \end{matrix}

Design Resistance of Beam Flange and Web in Compression

where
M_c,Rd	is the design resistance of the beam; assuming that the design shear force in the beam does not reduce M_c,Rd, therefore, M_c,Rd = 649 kN
h	= h_b = 533.1 mm
t_fb	= 15.6 mm

Thus, F_c,fb,Rd = 1254 kN.

Summary: resistance of compression zone
Column web in transverse compression F_c,wc,Rd = 841 kN, Beam flange and web in compression F_c,fb,Rd = 1254 kN.

Resistance of column web panel in shear
The plastic shear resistance of an unstiffened web is given by:

V_{w p, R d} = \begin{matrix} 0.9 f_{y, w c} A_{v c} \\ \sqrt{3} γ_{M 0} \end{matrix}

Resistance of Column Web Panel in Shear

The resistance is not evaluated here, as there is no design shear in the web because the moments from the beams are equal and opposite.

Moment Resistance

EFFECTIVE RESISTANCE OF BOLT ROWS

Force Distribution | Moment Resistance Analysis

The effective resistances of each of the three bolt rows in the tension zone are:
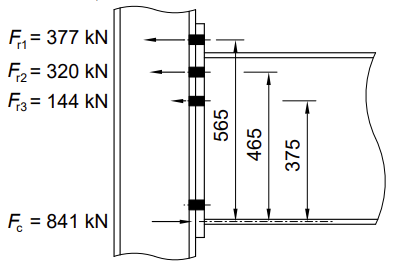
F_t1,Rd = 377 kN, F_t2,Rd = 320 kN, F_t3,Rd = 291 kN.

The effective resistances should be reduced if the resistance of one of the higher rows exceeds 1.9 F_t,Rd = 1.9 x 203 = 386 kN.
Thus, no reduction is necessary.

EQUILIBRIUM OF FORCES
The sum of the tensile forces, along with any axial compression in the beam, cannot exceed the resistance of the compression zone.
Similarly, the design shear cannot exceed the shear resistance of the column web panel. This is not relevant in this example, as the moments in the identical beams are equal and opposite.

For horizontal equilibrium ∑F_tr,Rd + N_Ed = F_c,Rd. In this example, there is no axial compression. Thus, ∑F_tr,Rd = F_c,Rd.

Here, the total effective tension resistance ∑F_tr,Rd = 377 + 320 + 291 = 988 kN which exceeds the compression resistance F_с,Rd = 841 kN.
To achieve equilibrium, the effective resistances are reduced, starting at the lowest row and working upward, until equilibrium is reached. Required reduction 988 - 841 = 147 kN.
All of this reduction can be achieved by reducing the resistance of the bottom row. Hence, F_t3,Rd = 291 - 147 = 144 kN.

Force equilibrium diagram showing balanced load vectors | engineering analysis

Force Equilibrium Diagram Analysis

MOMENT RESISTANCE OF FORCES
The moment resistance of the beam-to-column joint M_j,Rd:

M_{j, R d} = \sum h_{r} F_{t r, R d}

Moment Resistance of Beam-to-Column Joint

Taking the center of compression as the mid-thickness of the compression flange of the beam, h_r1 = 565 mm, h_r2 = 465 mm, h_r3 = 375 mm. Thus, the moment resistance of the beam-to-column joint is:

M_j,Rd = 416 kNm.

Vertical Shear Resistance

RESISTACNE OF THE BOLT GROUP
The shear resistance of a non-preloaded M24 class 8.8 bolt in single shear is F_v,Rd = 136 kN, F_b,Rd = 200 kN (in 20 mm ply). Thus, F_v,Rd governs.

The shear resistance of the upper rows may be taken conservatively as 28% of the shear resistance without tension (assuming that these bolts are fully utilized in tension). Thus, the shear resistance of all 4 rows is (2 + 6 x 0.28) 136 = 3.68 x 136 = 500 kN.

Weld Design

The simple approach requires that the welds to the tension flange and the web be of full strength, while the weld to the compression flange is of nominal size only, assuming it has been prepared with a sawn cut end.

BEAM TENSION FLANGE WELDS
A full-strength weld is provided by symmetrical fillet welds with a total throat thickness at least equal to the flange thickness. The required throat size is t_fb/2 = 15.6/2 = 7.8 mm. Weld throat provided is a_f = 12/√2 = 8.5 mm, which is adequate.

BEAM COMPRESSION FLANGE WELDS
Provide a nominal fillet weld on either side of the beam flange. An 8 mm leg length fillet weld will be satisfactory.

BEAM WEB WELDS
For convenience, a full-strength weld is provided to the web.
Required throat size is t_fw/2 = 10.2/2 = 5.1 mm.
Weld throat provided is a_p = 8/√2 = 5.7 mm, which is adequate.

COMPONENT BASED FE ANALYSIS

The design has been carried out using the Steel Joints Add-on for RFEM 6.
The Steel Joints add-on allows for the analysis of connections based on an FE model. The input and result evaluation are fully integrated into the user interface of the structural FEA software RFEM, making the design process intuitive and fast.

Joint Configuration

A steel joint is shown with clear connection details between steel members.

Steel Joint Overview | Connection Detail

Column	254x254x107 UKC	S275
Beam	parametrically defined section
	h_b = 533.1 mm, b_b = 209.3 mm, t_wb = 10.1 mm, t_fb = 15.6 mm	S275
End plate	670x250x25 mm	S275
Bolt	M24 class 8.8
Welds	Fillet welds top flange s_f1 = 8.5 mm, bottom flange s_f2 = 5.7 mm, web s_w = 5.7 mm

Steel Joints Add-on Outcomes

The Steel Joints Add-on for RFEM 6 enhances the software's capabilities by enabling engineers to analyze steel connections with the precision of a finite element (FE) model. This advanced tool allows for the detailed visualization of all essential results directly on the FE model, providing a clear and comprehensive overview of the performance of steel connections under various loads and conditions.

It includes the display of equivalent stresses and plastic strains within the steel connection. By showing both equivalent stresses and plastic strains, RFEM offers a more comprehensive understanding of the connection's behavior under real-world conditions, ensuring that the design is both safe and efficient.

EQUIVALENT STRESSES
Equivalent stresses provide a clear view of the overall stress distribution, helping engineers identify potential failure points caused by excessive stress concentrations. These stresses are essential for understanding the load-carrying capacity of the connection.

Visual representation of equivalent stresses on a joint, illustrating stress distribution and potential stress concentration areas.

Equivalent Stresses Shown on the Joint Geometry

Here, the stress distribution on the column flange and the beam end plate can be seen.

Visual representation of equivalent stress distribution on an end plate, showing color-coded stress variations.

Equivalent Stresses Shown on the End Plate

Visual representation of equivalent stress distribution on a column flange illustrating stress variations.

Equivalent Stresses Shown on the Column Flange

PLASTIC STRAIN
The plates in the connection are designed plastically by comparing the existing plastic strain to the allowable plastic strain. The default setting is 5%, according to EN 1993‑1‑5, Annex C. Below is the plastic strain in the joint:

The image displays plastic strain distribution on a joint structure with color gradients indicating deformation intensity.

Plastic Strain Shown on the Joint Geometry

STRESS-STRAIN ANALYSIS

Analysis of stress and strain distribution on structural plates, showcasing design check results to ensure compliance with standards.

Stress-Strain Analysis, Design Check for Plates

Illustration of stress-strain analysis results and weld design checks showcasing load-carrying capabilities in structural connections.

Stress-Strain Analysis, Design Check for Welds

Engineering analysis of fastener and connector design in a structural element using specialized software.

Design Check for Fasteners

Conclusions

The article presents two methods for designing beam-to-column joints. The analytical method is complex and challenging to handle manually, especially when it comes to optimization. It involves calculating the resistances of each component and comparing them to the forces acting on those components.

The second method is the CBFEM approach, implemented in the Steel Joints Add-on of RFEM 6. In this method, the joint is assembled, and the forces for analysis are derived from the main FE model. The assembled joint is then verified under the applied forces through stress-strain analysis of the steel plates. Additionally, the design of welds and fasteners is carried out according to the relevant EN standards.

While the analytical method is widely used, the second method is much faster, providing accurate results while significantly reducing computational time. It also enables easy and quick optimization.

A comparison of the results is shown below.
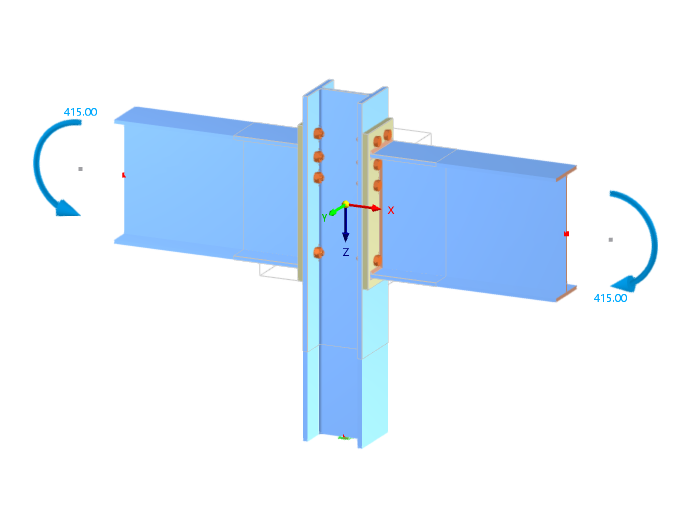
The moment resistance M_j,Rd calculated using the analytical approach is 416 kNm, while the value from CBFEM in the Steel Joints Add-on is 415 kNm. The difference is less than 1%, with Δ = -0.24%, illustrating the reliability and accuracy of the CBFEM method implemented in the Steel Joints Add-on.

The model can be found below:

Model 005595 | Unstiffened Bolted End Plate Connection

309x

86x

Unstiffened Bolted End Plate Connection

REFERENCES

[1] Brown, D., Iles, D., Brettle, M., Malik, A., and BCSA/SCI Connections Group. (2013). Joints in steel construction: Moment-resisting joints to Eurocode 3. Vol BCSA/SCI Connections Group. London: The British Constructional Steelwork Association Limited.

;