624x

001938

2025-04-01

未加劲螺栓端板连接

本文研究了在建筑中常用的无加劲螺栓端板连接这种常见的结构钢连接。基于欧码3指南的分析计算与从RFEM 6钢接头附加模块获得的结果进行了比较。重点是评估CBFEM方法在捕捉钢结构中的结构行为和载荷响应方面的准确性和可靠性。这项研究旨在加深对FEM软件表现的理解，为结构工程专业人员提供实用见解。

介绍

本文提供了根据Eurocode 3设计抗弯接头的指南，特别是针对多层框架中梁柱之间的螺栓端板连接。它引用了EN 1993-1-8和其他适用标准中的相关章节、图表和表格。

分析方法

分析程序取自[1]。

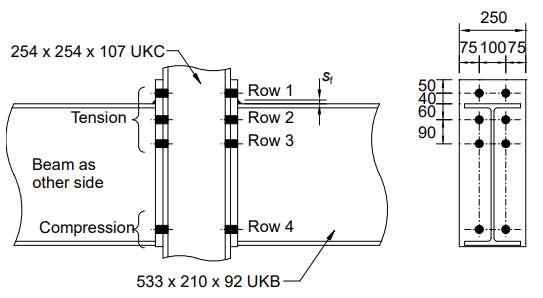
接头配置

钢节点设计图

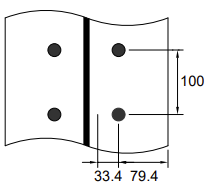
柱	254x254x107 UKC	S275
梁	533x210x92 UKB	S275
端板	670x250x25 mm	S275
螺栓	M24级 8.8
焊缝	角焊缝：法兰s_f = 12 mm，腹板s_w = 8 mm

等效T型接头的承载能力

评估等效T型接头的承载能力时，分别考虑端板和柱法兰。承载能力根据可能的三种失效模式进行计算，并取这些模式中最小的值。

每种模式下T型接头法兰的设计承载能力如下面所示。

钢节点破坏模式

以下展示了失效模式：

\begin{array}{l} 第一屈曲模态：完整的翼缘屈服 \\ F_{T, 1, R d} = \begin{matrix} (8 n - 2 e_{w}) M_{p l, 1, R d} \\ 2 m n - e_{w} (m + n) \end{matrix} \\ \begin{array}{l} 第二屈曲模态：螺栓失效，翼缘屈服 \\ F_{T, 2, R d} = \begin{array}{c} 2 M_{p l, 2, R d} + n (\sum F_{t, R d}) \\ m + n \end{array} \\ \begin{array}{l} 第三屈曲模态：螺栓失效 \\ F_{T, 3, R d} = \sum F_{t, R d} \end{array} \end{array} \end{array}

破坏形态

\begin{matrix} \begin{matrix} M_{p l, 1, R d} = \begin{array}{c} 0.25 \sum l_{e f f, 1} t_{f}^{2} f_{y} \\ γ_{M 0} \end{array}, \\ M_{p l, 2, R d} = \begin{array}{c} 0.25 \sum l_{e f f, 2} t_{f}^{2} f_{y} \\ γ_{M 0} \end{array} . \end{matrix} \end{matrix}

工字节点等效塑性抗弯矩（模态1和2）

其中
ℓ_eff,1	为模式1的等效T型接头的有效长度，取ℓ_eff,cp和ℓ_eff,nc中的较小值
ℓ_eff,2	为模式2的等效T型接头的有效长度，取ℓ_eff,nc
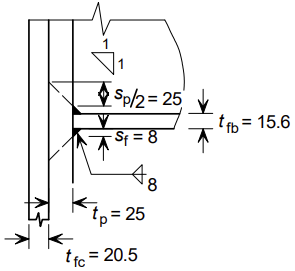
t_f	为T型接头法兰厚度（= t_p或t_fc）
f_y	为T型接头法兰的屈服强度（例如柱或端板）
∑F_t,Rd	为T型接头中螺栓的总拉力承载能力（= 2F_t,Rd对于单排）
e_w	= d_w/4
d_w	为垫圈直径或螺栓头宽度
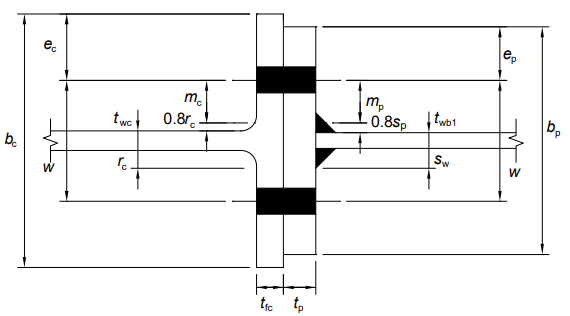
m	为图中定义的距离
n	为e_c（柱法兰边距）、e_p（端板边距）、1.25 m（对于端板或柱法兰，适用于适当的情况）中最小的值

承载能力定义：

\begin{array}{l} Resistance of column flange in bending \\ F_{t, f c, R d} = \min {F_{T, 1, R d}, F_{T, 2, R d}, F_{T, 3, R d}} \\ \begin{array}{l} Resistance of an unstiffened column web to transverse tension \\ F_{t, w c, R d} = \begin{array}{c} ω b_{e f f, t, w c} t_{w c} f_{y, w c} \\ γ_{M 0} \end{array} \\ Resistance of the end plate in bending \\ F_{t, e p, R d} = \min {F_{T, 1, R d}, F_{T, 2, R d}, F_{T, 3, R d}} \\ \begin{matrix} \begin{array}{l} Resistance of the beam web \\ F_{t, w b, R d} = \begin{array}{c} b_{e f f, t, w b} t_{w b} f_{y, b} \\ γ_{M 0} \end{array} \end{array} \end{matrix} \end{array} \end{array}

柱翼缘抗弯设计

拉伸区T型接头

螺栓排1
柱法兰在弯曲中（无背板）
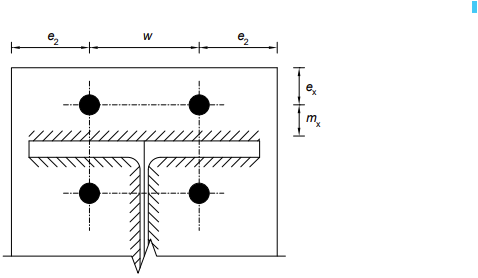
仅考虑螺栓排1的作用。关键尺寸如下所示。

T 形受拉连接节点详图

端板在弯曲中

T 形板关键尺寸概览

承载能力计算摘要：

参数	单位	柱法兰在弯曲中（无背板）	柱腹板横向拉伸中	端板在弯曲中	梁腹板在拉伸中
m	[mm]	33.4	-	= m_x = 30.4	-
e	[mm]	= e_min = 75	-	e = 75, e_x = 50	-
ℓ_eff,1	[mm]	210	-	125	-
ℓ_eff,2	[mm]	233	-	125	-

模式1
n	[mm]	41.8	-	38.0	-
t_f	[mm]	20.5	-	25	-
f_y	[N/mm²]	265	-	265	-
M_pl,1,Rd	[Nmm]	5850x10³	-	5180x10³	-
d_w	[mm]	39.55	-	-	-
e_w	[mm]	9.9	-	9.9	-
F_T,1,Rd	[kN]	898	-	901	-

模式2
M_pl,2,Rd	[Nmm]	6490x10³	-	5180x10³	-
F_t,Rd	[N]	203x10³	-	203x10³	-
螺栓排列	[pcs]	2	-	2	-
∑F_t,Rd	[N]	406x10³	-	406x10³	-
F_T,2,Rd	[kN]	398	-	377	-

模式3
F_T,3,Rd	[kN]	406	-	406	-

ω	[-]	-	1.0	-
b_eff,t,wc	[mm]	-	= ℓ_eff,2 = 233	-
f_y,wc	[N/mm²]	-	= f_y,c = 265	-

承载能力		F_t,fc,Rd	F_t,wc,Rd	F_t,ep,Rd
	[kN]	398	790	377
注意					不适用

螺栓排1的承载能力是上述承载能力中的最小值。因此，F_t,1,Rd = min {F_t,fc,Rd = 398; F_t,wc,Rd = 790; F_t,ep,Rd = 377} = 377 kN。

螺栓排2
首先，仅考虑第2排。

端板在弯曲中
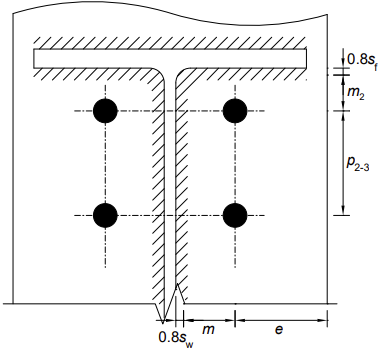
螺栓排2是梁法兰下的第一排螺栓，视为“梁的张力法兰下的第一排螺栓”。柱法兰T型接头的关键尺寸在第1排和第2排的图示中显示。

T-Stub 尺寸表第 2 行

承载能力计算摘要：

参数	单位	柱法兰在弯曲中	柱腹板在横向拉伸中	端板在弯曲中	梁腹板在拉伸中
m	[mm]	-	-	= m_p = 38.6	-
m₂	[mm]	-	-	34.8	-
e	[mm]	-	-	= e_p = 75	-
ℓ_eff,1	[mm]	-	-	243	-
ℓ_eff,2	[mm]	-	-	290	-

模式1
n	[mm]	-	-	48.3	-
t_f	[mm]	-	-	25	-
f_y	[N/mm²]	-	-	265	-
M_pl,1,Rd	[Nmm]	-	-	10.1x10³	-
e_w	[mm]	-	-	9.9	-
F_T,1,Rd	[kN]	-	-	1291	-

模式2
M_pl,2,Rd	[Nmm]	-	-	12.0x10⁶	-
F_t,Rd	[N]	-	-	203x10³	-
螺栓排列	[pcs]	-	-	2	-
∑F_t,Rd	[N]	-	-	406x10³	-
F_T,2,Rd	[kN]	-	-	502	-

模式3
F_T,3,Rd	[kN]	-	-	406	-

ω	[-]	-	-	-	1.0
b_eff,t,wc	[mm]	-	-	-	243
t_wb	[mm]	-	-	-	10.1
f_y,wc	[N/mm²]	-	-	-	675

承载能力		F_t,fc,Rd	F_t,wc,Rd	F_t,ep,Rd	F_t,wb,Rd
	[kN]	398	790	406	675
注意	如第1排螺栓时计算	如第1排螺栓时计算

以上第2排的承载能力都考虑了排独自作用。然而，在柱侧，承载能力可能会受到第1排和第2排组合承载能力的限制。现在考虑组合承载能力。

第1排和第2排组合
柱法兰在弯曲中

第 1 行和第 2 行间距细节

承载能力计算摘要：

参数	单位	柱法兰在弯曲中	柱腹板在横向拉伸中	端板在弯曲中
m	[mm]	33.4	-	-
ℓ_eff,1	[mm]	332	-	-
ℓ_eff,2	[mm]	332	-	-

模式1
n	[mm]	41.8	-	-
t_f	[mm]	20.5	-	-
f_y	[N/mm²]	265	-	-
M_pl,1,Rd	[Nmm]	9.24x10³	-	-
e_w	[mm]	9.9	-	-
F_T,1,Rd	[kN]	1420	-	-

模式2
M_pl,2,Rd	[Nmm]	9.24x10⁶	-	-
F_t,Rd	[N]	203	-	-
螺栓	[pcs]	4	-	-
∑F_t,Rd	[N]	812	-	-
F_T,2,Rd	[kN]	697	-	-

模式3
F_T,3,Rd	[kN]	812	-	-

ω	[-]	-	1.0	-
b_eff,t,wc	[mm]	-	332	-
t_wb	[mm]	-	12.8	-
f_y,wc	[N/mm²]	-	265	-

承载能力		F_t,fc,Rd	F_t,wc,Rd	F_t,ep,Rd
	[kN]	697	1126	-
注意				端板没有组合模式

螺栓排1和排2的承载能力是“柱法兰在弯曲”和“柱腹板在拉伸”的最小值，即F_t,1-2,Rd = min {F_t,fc,Rd = 697; F_t,wc,Rd = 1126} = 697 kN。
因此，第2排螺栓在柱侧的承载能力限制为F_t2,c,Rd = F_t,1-2,Rd - F_t1,Rd = 697 - 377 = 320 kN。

第2排螺栓的承载能力是下列承载能力的最小值：“柱法兰在弯曲”F_t,fc,Rd = 398 kN，“柱腹板在拉伸”F_t,wc,Rd = 790 kN，“梁腹板在拉伸”F_t,wb,Rd = 675 kN，“端板在弯曲”F_t,ep,Rd = 406 kN 和“柱侧”作为组合的一部分，F_t2,c,Rd = 320 kN。因此，第2排螺栓的承载能力F_t,2,Rd = 320 kN。

螺栓排3
首先，仅考虑第3排。

承载能力计算摘要：

参数	单位	柱法兰在弯曲中	柱腹板在横向拉伸中	端板在弯曲中	梁腹板在拉伸中
e	[mm]	-	-	= e_p = 75	-
m	[mm]	-	-	38.6	-
ℓ_eff,1	[mm]	-	-	248	-
ℓ_eff,2	[mm]	-	-	248	-

模式1
n	[mm]	-	-	48.3	-
t_f	[mm]	-	-	25	-
f_y	[N/mm²]	-	-	265	-
M_pl,1,Rd	[Nmm]	-	-	10.1x10⁶	-
e_w	[mm]	-	-	9.9	-
F_T,1,Rd	[kN]	-	-	1291	-

模式2
M_pl,2,Rd	[Nmm]	-	-	10.3x10⁶	-
F_t,Rd	[N]	-	-	203	-
螺栓	[pcs]	-	-	2	-
∑F_t,Rd	[N]	-	-	406	-
F_T,2,Rd	[kN]	-	-	463	-

模式3
F_T,3,Rd	[kN]	-	-	406	-

b_eff,t,wb	[mm]	-	-	-	= b_eff,1 = 243
t_wb	[mm]	-	-	-	10.1

承载能力		F_t,fc,Rd	F_t,wc,Rd	F_t,ep,Rd	F_t,wb,Rd
	[kN]	790	790	406	675
注意	如第1排和第2排螺栓时计算	如第1排和第2排螺栓时计算

第2排和第3排的承载能力都考虑了排独自作用。然而，在柱侧，承载能力可能会受到第1、2和3排组合或第2和3排组合的限制。在梁侧，承载能力可能会受到第2和3排组合的限制。现在考虑这些组合承载能力。

螺栓1, 2和3组合
柱法兰在弯曲中
圆形和非圆形图案如下：

圆形和非圆形屈服线模式

承载能力计算摘要：

参数	单位	柱法兰在弯曲中	柱腹板在横向拉伸中
ℓ_eff,1	[mm]	422	-
ℓ_eff,2	[mm]	422	-

模式1
m	[mm]	33.4	-
n	[mm]	41.8	-
e_w	[mm]	9.9	-
t_f	[mm]	20.5	-
f_y	[N/mm²]	265	-
M_pl,1,Rd	[Nmm]	11.7x10⁶	-
F_T,1,Rd	[kN]	1797	-

模式2
M_pl,2,Rd	[Nmm]	11.7x10⁶	-
F_t,Rd	[kN]	203	-
螺栓	[pcs]	6	-
∑F_t,Rd	[kN]	1218	-
F_T,2,Rd	[kN]	988	-

模式3
F_T,3,Rd	[kN]	1218	-

ω	[-]	-	1.0
b_eff,t,wc	[mm]	-	422
t_wc	[mm]	-	12.8

承载能力		F_t,fc,Rd	F_t,wc,Rd
	[kN]	988	1431

柱侧螺栓排1,2,3组合的承载能力是“柱法兰在弯曲”和“柱腹板在拉伸”的最小值，即988 kN。
因此，第3排螺栓在柱侧的承载能力限制为：F_t3,c,Rd = F_t1-3,Rd - F_t1-2,Rd = 988 - 697 = 291 kN。

第2排和第3排组合
承载能力计算摘要：

参数	单位	柱侧–法兰在弯曲中	柱腹板在横向拉伸中	梁侧–端板在弯曲中	梁在拉伸中
m	[mm]	33.4	-	38.6	-
n	[mm]	41.8	-	48.3	-
e_w	-	-	9.9	-
ℓ_eff,1	[mm]	323	-	379	-
ℓ_eff,2	[mm]	323	-	379	-

模式1			(第2+3排)
M_pl,1,Rd	[Nmm]	9.24x10³	9.0x10⁶	15.7x10⁶	-
F_T,1,Rd	[kN]	1383	-	2007	-

模式2			(第2+3排)
M_pl,2,Rd	[Nmm]	9.0x10⁶	-	15.7x10⁶	-
F_t,Rd	[kN]	203	-	203	-
螺栓	[pcs]	4	-	4	-
∑F_t,Rd	[kN]	812	-	812	-
F_T,2,Rd	[kN]	691	-	813	-

模式3			(第2+3排)
F_T,3,Rd	[kN]	1218	-	812	-

ω	[-]	-	1.0	-	-
b_eff,t,wc	[mm]	-	323	-	-
t_wb	[mm]	-	12.8	-	-
f_y,wc	[N/mm²]	-	265	-	-

承载能力		F_t,fc,Rd	F_t,wc,Rd	F_t,ep,Rd
	[kN]	691	1096	812	-
注意					不适用

梁侧螺栓排2和3组合的承载能力是“端板在弯曲中”F_t,ep,Rd = 812 kN。因此，梁侧F_t2-3,Rd = 812 kN。第3排螺栓在梁侧的承载能力限制为F_t3,b,Rd = F_t2-3,Rd - F_t2,Rd = 812 - 320 = 492 kN。

柱侧螺栓排2和3组合的承载能力是“柱法兰在弯曲中”F_t,fc,Rd = 691 kN，“柱腹板在拉伸中”F_t,wc,Rd = 1096 kN，因此，柱侧F_t2-3,Rd = 691 kN。
因此，第3排螺栓在柱侧的承载能力限制为F_t3,b,Rd = F_t2-3,Rd - F_t2,Rd = 691 - 320 = 371 kN。

总结
第3排螺栓的承载能力是以下承载能力中的最小值：“柱法兰在弯曲中”F_t,fc,Rd = 398 kN，“柱腹板在拉伸中”F_t,wc,Rd = 790 kN，“梁腹板在拉伸中”F_t,wb,Rd = 675 kN，“端板在弯曲中”F_t,ep,Rd = 406 kN，“柱侧作为与组合作为第2和第1的一部分”F_t3,c,Rd = 291 kN，“柱侧作为与第2组合的一部分”F_t3,c,Rd = 371 kN，“梁侧作为与第2组合的一部分”F_t3,b,Rd = 492 kN。因此，第3排螺栓的承载能力是F_t3,Rd = 291 kN。

拉伸承载能力总结
上面导出的拉伸排的有效承载能力可总结为表格形式，如下所示。

排的承载能力F_tr,Rd:

	柱法兰	柱腹板	端板	梁腹板	最小值	有效承载能力
第1排，单独	398	790	377	不适用	377	377

第2排，单独	398	790	406	675	398
第2排，与第1排	697	1126	不适用	不适用	697
第2排					697 - 377	320

第3排，单独	398	790	406	675	309
第3排，与第1和2排	988	1431	不适用	不适用	988
第3排					988 - 697	291
第3排，与第2排	691	1096	812	1052	691
第3排					691 - 320

压缩区

柱腹板在横向压缩中
未加固柱腹板在横向压缩中的设计承载能力如下确定：

压溃承载力：

F_{c, w c, R d} = \begin{array}{c} ω k_{w c} b_{e f f, c, w c} t_{w c} f_{y, w c} \\ γ_{M 0} \end{array}, 但 (屈曲承载力)： F_{c, w c, R d} \leq \begin{array}{c} ω k_{w c} ρ b_{e f f, c, w c} t_{w c} f_{y, w c} \\ γ_{M 1} \end{array} .

横向受压柱腹板

其中
s	= r_c = 12.7 mm对于热轧I型和H型柱截面
s_p	通过端板以45°扩散得到的长度；s_p = 2 t_p = 50 mm
e_x	从第1排紧固件中心测量的端距离；e_x = 50 mm
x	从紧固件中心测量的梁法兰上方第1排的间距；x = 40 mm
s_f	焊缝腿部长度；s_f = 8 mm
h_p	端板的深度；h_p ≥ e_x + x + h_b + s_f + t_p = 656 mm → h_p = 670 mm
b_eff,c,wc	螺栓端板；b_eff,c,wc = t_fb + 2 s_f + 5 (t_fc + s) + s_p = 248 mm
ρ	为板屈曲的减小系数，取决于板；ρ = 1.0
ω	= 1.0
k_wc	是一个减小系数，考虑柱腹板中的压缩；k_wc = 1.0

螺栓端板尺寸

因此，F_c,wc,Rd = 841 kN。

梁法兰和腹板在压缩中
梁法兰和相邻压缩区腹板的最终设计承载能力使用以下方法确定：

F_{c, f b, R d} = \begin{matrix} M_{c, R d} \\ h - t_{f b} \end{matrix}

梁翼缘和腹板受压承载力设计值

其中
M_c,Rd	为梁的设计承载能力；假设梁中的设计剪力不减少M_c,Rd，因此，M_c,Rd = 649 kN
h	= h_b = 533.1 mm
t_fb	= 15.6 mm

因此，F_c,fb,Rd = 1254 kN。

压缩区的承载能力总结
柱腹板在横向压缩中 F_c,wc,Rd = 841 kN，梁法兰和腹板在压缩中 F_c,fb,Rd = 1254 kN。

柱腹板面板在剪切中的承载能力
未加固腹板的塑性剪切承载能力见下式：

V_{w p, R d} = \begin{matrix} 0.9 f_{y, w c} A_{v c} \\ \sqrt{3} γ_{M 0} \end{matrix}

柱腹板受剪承载力

这里不评估承载能力，因为腹板中没有设计剪力，因为梁的力矩是相等且相反的。

力矩承载能力

螺栓排的有效承载能力

力分布

拉伸区中每个三排螺栓的有效承载能力为：
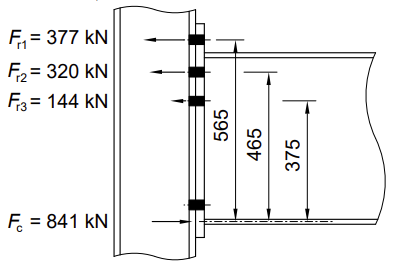
F_t1,Rd = 377 kN, F_t2,Rd = 320 kN, F_t3,Rd = 291 kN。

如果较高排的承载能力超过1.9 F_t,Rd = 1.9 x 203 = 386 kN，则有效承载能力应降低。
因此，不需要降低。

力的平衡
拉力的总和，不包括梁中的任何轴向压缩，不能超过压缩区承载能力。
同样，设计剪力不能超过柱腹板面板的剪切承载能力。在此示例中不适用，因为相同的梁中的力矩是相等且相反的。

对于水平方向的平衡 ∑F_tr,Rd + N_Ed = F_c,Rd。在此示例中，没有轴向压缩。因此，∑F_tr,Rd = F_c,Rd。

这里，总有效拉力承载能力 ∑F_tr,Rd = 377 + 320 + 291 = 988 kN 超过了压缩承载能力 F_с,Rd = 841 kN。
为了达到平衡，从最低排开始进行有效承载能力的降低，向上进行，直到达到平衡。所需减少988 - 841 = 147 kN。
所有这些减少可以通过减少底排的承载能力来实现。因此，F_t3,Rd = 291 - 147 = 144 kN。

力平衡图分析

力矩承载能力
梁柱接头的力矩承载能力 M_j,Rd：

M_{j, R d} = \sum h_{r} F_{t r, R d}

梁柱节点的抗弯能力

假设压缩中心为梁压缩法兰的中厚度，h_r1 = 565 mm, h_r2 = 465 mm, h_r3 = 375 mm。因此，梁柱接头的力矩承载能力为：

M_j,Rd = 416 kNm.

垂直剪力承载能力

螺栓组的承载能力
未预紧的M24 8.8级螺栓在单剪中承载能力 F_v,Rd = 136 kN, F_b,Rd = 200 kN (在20 mm层)。因此，F_v,Rd 起决定性作用。

可以保守地将上排的剪力承载能力视为无张力状态下剪力承载能力的28%（假设这些螺栓在张力中完全利用）。因此，所有4排的剪力承载能力为 (2 + 6 x 0.28) 136 = 3.68 x 136 = 500 kN。

焊接设计

简单的方法要求张力法兰和腹板的焊缝为全强度，而压缩法兰的焊缝仅为名义尺寸，假设其已准备了锯切端。

梁张力法兰焊接
通过对称的角焊缝提供全强度焊接，焊缝总厚度至少等于法兰厚度。所需的焊缝厚度为t_fb/2 = 15.6/2 = 7.8 mm。提供的焊缝厚度为a_f = 12/√2 = 8.5 mm，足够。

梁压缩法兰焊接
在梁法兰的任一侧提供名义的角焊缝。8 mm的焊缝腿部长度将是满意的。

梁腹板焊接
为方便，腹板提供全强度焊接。
所需的焊缝厚度为t_fw/2 = 10.2/2 = 5.1 mm。
提供的焊缝厚度为a_p = 8/√2 = 5.7 mm，足够。

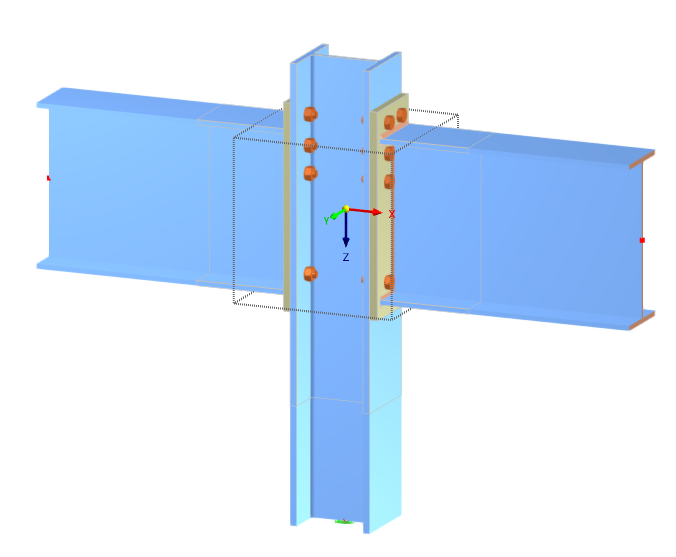
基于组件的有限元分析

设计已使用RFEM 6的钢接头附加组件进行。
钢接头附加组件允许基于有限元模型的连接分析。输入和结果评估完全集成到结构FEA软件RFEM的用户界面中，使设计过程直观且快速。

接头配置

钢节点概览 | 连接细节

柱	254x254x107 UKC	S275
梁	参数化定义截面
	h_b = 533.1 mm, b_b = 209.3 mm, t_wb = 10.1 mm, t_fb = 15.6 mm	S275
端板	670x250x25 mm	S275
螺栓	M24 8.8级
焊缝	上法兰角焊缝s_f1 = 8.5 mm, 下法兰s_f2 = 5.7 mm, 腹板s_w = 5.7 mm

钢接头附加功能的结果

RFEM 6的钢接头附加功能通过启用工程师使用有限元（FE）模型分析钢连接来增强软件的功能。此高级工具允许在FE模型上直接详细查看所有重要结果，提供了关于在各种荷载和条件下钢连接性能的清晰而全面的概览。

它还包括在钢连接中显示等效应力和塑性应变。通过显示等效应力和塑性应变，RFEM提供了更全面的关于连接在真实世界条件下行为的理解，确保设计既安全又高效。

等效应力
等效应力提供了整体应力分布的清晰视图，帮助工程师识别由过度应力集中引起的潜在失效点。这些应力对于理解连接的承载能力至关重要。

显示在节点几何形状上的当量应力

这里可以看到柱法兰和梁端板上的应力分布。

端板上的等效应力

Equivalent Stresses Shown on the Column Flange

塑性应变
通过将现存的塑性应变与允许的塑性应变进行比较，设计连接中的板材。根据EN 1993‑1‑5, 附录C，默认设置为5%。下面显示了接头中的塑性应变：

接头几何形状上的塑性应变

应力-应变分析

应力-应变分析, 板的设计验算

应力-应变分析, 焊缝设计验算

紧固件的设计验算

结论

本文展示了设计梁柱接头的两种方法。分析方法复杂且难以手动处理，特别是在进行优化时。它涉及计算每个构件的承载能力，并将其与作用在这些构件上的力进行比较。

第二种方法是RFEM 6中钢接头附加组件中实现的CBFEM方法。在此方法中，结合接头，并从主FE模型中导出分析力。然后通过钢板的应力-应变分析验证组合接头在施加力下的性能。此外，焊缝和紧固件的设计根据相关的EN标准进行。

虽然分析方法广泛使用，但第二种方法速度更快，提供准确的结果，同时显著减少计算时间。它还便于快速和轻松地优化。

下文显示了结果比较。
通过分析方法计算的力矩承载力M_j,Rd为416 kNm，而在钢接头附加组件中CBFEM的值为415 kNm。差异小于1%，Δ = -0.24%，显示出在钢接头附加组件中实施的CBFEM方法的可靠性和准确性。

模型请见下面：

309x

86x

Unstiffened Bolted End Plate Connection

参考文献

[1] Brown, D., Iles, D., Brettle, M., Malik, A.，和 BCSA/SCI Connections Group. (2013). Joints in steel construction: Moment-resisting joints to Eurocode 3. Vol BCSA/SCI Connections Group. London: The British Constructional Steelwork Association Limited.

;