Instrukcje online RFEM 6 | Powierzchnie wielowarstwowe

Powrót do Instrukcji online

2263x

003626

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

2023-10-19

Wybór ręczny

Przegląd

Rozszerzenie Powierzchnie wielowarstwowe

Teoria

Wprowadzanie danych

Wyniki

Przykłady obliczeń

Sztywności powierzchni wielowarstwowych

Modele materiałowe

Podstawą do zestawienia wielowarstwowych powierzchni w efektywną sztywność powierzchni są modele materiałowe. Za pomocą dodatku Powierzchnie wielowarstwowe można swobodnie łączyć modele materiałowe w programie RFEM 6. Podstawy modeli materiałowych znajdują się w rozdziałach Materiały oraz Nieliniowe zachowanie materiału podręcznika RFEM.

Wyboru możliwości kombinacji modeli materiałowych można dokonać w modelu "Modele wielowarstwowe" (patrz prawa kolumna), który można pobrać w celu dalszego studiowania kombinacji.

Poniższa lista pokazuje wybór możliwych kombinacji:

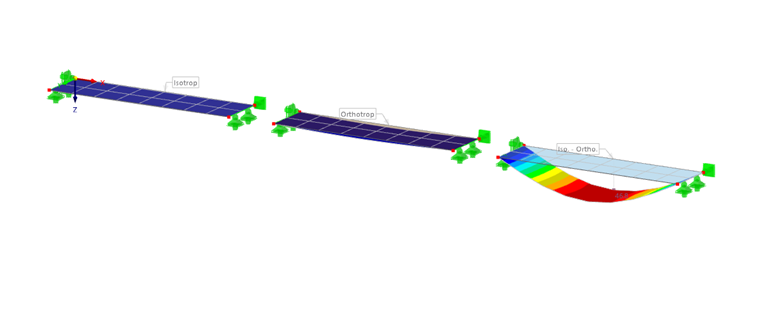
Warstwy izotropowe (np. beton - stal)
Warstwy ortotropowe (np. CLT - Cross Laminated Timber)
Izotropowe - ortotropowe (np. stal - GFK)
Izotropowe plastyczne - izotropowe (np. beton - stal)
Izotropowe nieliniowo sprężyste - ortotropowe (np. beton - drewno)
Izotropowe - ortotropowo plastyczne (np. beton - drewno)
Izotropowe uszkodzenie - ortotropowe (np. beton - drewno)

Informacje

Dla kombinacji nieliniowych materiałów musi być aktywowany dodatek Nieliniowe zachowanie materiału.

Sztywności w wielowarstwowych powierzchniach bez objętości

Prostszym wariantem obliczeniowym w dodatku Powierzchnie wielowarstwowe jest zdefiniowanie różnych warstw powierzchni w typie grubości 'Warstwy' bez uwzględnienia objętości. Również tutaj można swobodnie łączyć modele materiałowe.

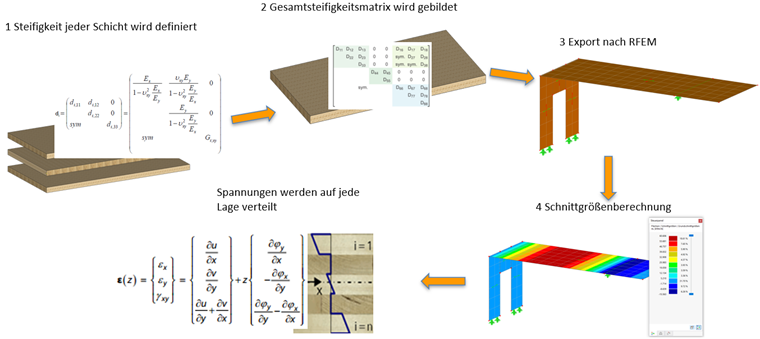
Gdy warstwy są zdefiniowane, dodatek Powierzchnie wielowarstwowe generuje globalną macierz sztywności powierzchni. W RFEM dla tej powierzchni obliczane są siły wewnętrzne i odkształcenia. W odpowiednich dodatkach do projektowania, takich jak np. Projektowanie drewna lub obliczenia sił-odkształceń, te siły wewnętrzne są następnie rozdzielane na obecne warstwy. Zwykle siły wewnętrzne są przedstawiane na trzech punktach integracyjnych na warstwę.

Przebieg obliczeń dla powierzchni wielowarstwowych

Proces obliczania powierzchni wielowarstwowych

Poniżej przedstawiono obliczanie macierzy sztywności dla materiałów izotropowych i ortotropowych.

Obliczanie macierzy sztywności

Podstawą modeli materiałowych są następujące warunki (patrz także rozdział Materiały podręcznika RFEM):

Wszystkie wartości sztywności ≥ 0
Całkowita macierz sztywności powierzchni musi być dodatnio określona.
Równanie podstawowe dla izotropu:

E = 2 G (1 + ν)

E	Moduł sprężystości
G	Moduł ścinania
ν	Współczynnik Poissona

Moduł sprężystości, moduł ścinania i współczynnik Poissona{

Równanie podstawowe dla ortotropu:

\frac{ν_{y x}}{E_{y}} = \frac{ν_{x y}}{E_{x}}

Zależność odkształcenia poprzecznego

Lokalna macierz sztywności każdej warstwy

Izotropowe

d_{i}' = [\begin{matrix} d'_{11, i} & d'_{12, i} & 0 \\ d'_{22, i} & 0 \\ s y m . & d'_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{i}}{1 - ν_{i}^{2}} & \frac{ν_{i} E_{i}}{1 - ν_{i}^{2}} & 0 \\ \frac{E_{i}}{1 - ν_{i}^{2}} & 0 \\ s y m . & G_{i} \end{matrix}] i = 1, . . ., n m i t G_{i} = \frac{E_{i}}{2 (1 + ν_{i})}

Warstwa macierzy sztywności izotropowa

Ortotropowe

d_{i}' = [\begin{matrix} d'_{11, i} & d'_{12, i} & 0 \\ d'_{22, i} & 0 \\ s y m . & d'_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{x, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & \frac{ν_{x y, i} E_{y, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ \frac{E_{y, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ s y m . & G_{x y, i} \end{matrix}] i = 1, . . ., n

Ortotropowa warstwa macierzy sztywności

Informacje

Dla materiału ortotropowego moduł ścinania w płaszczyźnie płyty (G_xy) jest definiowany poprzez wartości materiałowe, podczas gdy dla materiału izotropowego jest obliczany z modułu Younga i wyniosłości poprzecznej. Dlatego dla materiału ortotropowego relacja wyniosłości poprzecznej z zasadą "miejsce-przyczyna" jest ważna.

Sztywności przy ścinaniu dla materiału ortotropowego są następujące:

G_xy	Moduł ścinania w płaszczyźnie płyty (np. 690 N/mm² dla C24)
G_xz	Moduł ścinania w kierunku x przez grubość (np. 690 N/mm² dla C24)
G_yz	Moduł ścinania w kierunku y przez grubość (np. 690 N/mm² dla C24) – nazywany również modułem środkowego ścinania

Dla materiału ortotropowego występuje również możliwość definiowania skierowanych sztywności w powierzchni. W standardowym przypadku lokalna orientacja powierzchni lub warstwy w kierunku x odpowiada sztywności w kierunku x. Ponieważ jednak można ją dowolnie definiować poprzez kąt β w typie grubości 'Warstwy', należy odpowiednio transformować sztywności.

d_{i} = [\begin{matrix} d_{11, i} & d_{12, i} & d_{13, i} \\ d_{22, i} & d_{23, i} \\ s y m . & d_{33, i} \end{matrix}] = T_{3 x 3, i}^{T} d'_{i} T_{3 x 3, i}

Sztywności transformacji

T_{3 x 3, i} = [\begin{matrix} c ² & s ² & c s \\ s ² & c ² & - c s \\ - 2 c s & 2 c s & c ² - s ² \end{matrix}] m i t c = \cos (β_{i}), s = \sin (β_{i})

Macierz transformacji

Dodany element każdej warstwy:

d_{11, i} = c^{4} d'_{11, i} + 2 c ² s ² d'_{12, i} + s^{4} d'_{22, i} + 4 c ² s ² d'_{33, i}

d_{12, i} = c^{2} s^{2} d'_{11, i} + s^{4} d'_{12, i} + c^{4} d'_{12, i} + c ² s ² d'_{22, i} - 4 c ² s ² d'_{33, i}

d_{13, i} = c^{3} s d'_{11, i} + c s^{3} d'_{12, i} - c^{3} s d'_{12, i} - c s^{3} d'_{22, i} - 2 c^{3} s d'_{33, i} + 2 c s^{3} d'_{33, i}

d_{22, i} = s^{4} d'_{11, i} + 2 c ² s ² d'_{12, i} + c^{4} d'_{22, i} + 4 c ² s ² d'_{33, i}

d_{23, i} = c s^{3} d'_{11, i} + c^{3} s d'_{12, i} - c s^{3} d'_{12, i} - c^{3} s d'_{22, i} + 2 c^{3} s d'_{33, i} - 2 c s^{3} d'_{33, i}

d_{33, i} = c^{2} s^{2} d'_{11, i} - 2 c ² s ² d'_{12, i} + c^{2} s^{2} d'_{22, i} + {(c^{2} - s^{2})}^{2} d'_{33, i}

Poszczególne warunki na zmianę

Elementy zginające i skrętne [Nm]

Elementy macierzy dla zginania i skręcania są podane w poniższych równaniach.

D_{11} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{11, i}

Sztywność na zginanie w x

D_{12} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{12, i}

Wyrażenie mimośrodu (12)

D_{22} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{22, i}

Sztywność na zginanie w y

D_{13} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{13, i}

Wyrażenie mimośrodu (13)

D_{23} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{23, i}

Wyrażenie mimośrodu (23)

D_{33} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{33, i}

sztywność skrętna

W przypadku tylko jednej warstwy w typie grubości 'Warstwy', obliczenia są przeprowadzane zgodnie z równaniami wyjaśnionymi w podręczniku RFEM.

Dla ścinania (elementy D44/55) w typie grubości 'Warstwy' stosuje się inne równania, które zostaną omówione w sekcji Ścinanie w płaszczyźnie płyty.

Terminy ekscentryczności [Nm/m]

Dla asymetrycznych płyt pojawiają się terminy ekscentryczności. Asymetryczna powierzchnia może wystąpić na przykład podczas obliczania ochrony przeciwpożarowej poprzez jednostronne spalanie płyty CLT. Elementy macierzy są następujące:

D_{16} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{11, i}

Element mimośrodu D16

D_{17} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{12, i}

Element mimośrodu D17

D_{18} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{13, i}

Element mimośrodu D18

D_{27} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{22, i}

Element mimośrodowy D27

D_{28} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{23, i}

Element mimośrodowy D28

D_{38} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{33, i}

Element mimośrodu D38

Płaszczyzna dysku [N/m]

W płaszczyźnie dysku traktowane są sztywności normalne w płaszczyźnie płyty. Za pomocą elementu D88 obliczany jest poprzeczny ścinanie – czyli siła poprzeczna w płycie. Elementy macierzy są następujące:

D_{66} = \sum_{i = 1}^{n} t_{i} d_{11, i}

Sztywność osiowa x D66

D_{67} = \sum_{i = 1}^{n} t_{i} d_{12, i}

Sztywność normalna Mimośród D67

D_{68} = \sum_{i = 1}^{n} t_{i} d_{13, i}

Sztywność normalna Mimośród D68

D_{77} = \sum_{i = 1}^{n} t_{i} d_{22, i}

Sztywność osiowa y D77

D_{78} = \sum_{i = 1}^{n} t_{i} d_{23, i}

Sztywność normalna Mimośród D78

D_{88} = \sum_{i = 1}^{n} t_{i} d_{33, i}

Ścinanie płyty D88

Ścinanie w płaszczyźnie płyty [N/m]

Aby określić sztywność ścinania, dla materiału ortotropowego należy przekręcić sztywności w odniesieniu do ich orientacji względem lokalnej osi powierzchniowej. Należy to zrobić dla każdej warstwy typu grubości 'Warstwy'. W przypadku prostego układu warstwowego z orientacją 0° dla warstwy górnej i 90° dla poniższej warstwy, powstaje duża podatność na ścinanie, która musi być odpowiednio uwzględniona w modelu wielowarstwowym. Na poniższym obrazie (źródło [1]) jest to widoczne na przykładzie płyty CLT.

Ilustracja odkształcenia ścinającego w drewnie klejonym krzyżowo, udostępniona przez Informationsdienst Holz

Odkształcenie ścinania (źródło: Informationsdienst Holz)

W teorii laminatów sztywność ścinania układu warstwowego oblicza się poprzez transformację wszystkich składników według gięcia i ścinania w odpowiednie kierunki każdej warstwy. Więcej informacji na ten temat można znaleźć w podanej poniżej literaturze.

Wizualizacja orientacji osi sztywności w laminacie celem optymalizacji właściwości materiału

Orientacja sztywności

Poprzez przedstawioną na obrazie transformację sztywności sumuje się sztywności. To sumowanie jest również znane jako "całka Grashoffa".

D_{44, c a l c}^{"} = \frac{1}{\int_{- t / 2}^{t / 2} \frac{G_{22}^{"} (z)}{G_{11}^{"} (z) G_{22}^{"} (z) - {G_{12}^{"}}^{2} (z)} {(\frac{\int_{z}^{t / 2} E_{x}^{"} (\bar{z}) (\bar{z} - z_{0, x}) d \bar{z}}{\int_{- t / 2}^{t / 2} E_{x}^{"} (\bar{z}) {(\bar{z} - z_{0, x})}^{2} d \bar{z}})}^{2} d z}

Sztywność na ścinanie w kierunku x

Aby obliczyć sztywność w kierunku x i y, dla każdego układu wielowarstwowej powierzchni oblicza się tak zwany punkt sztywnościowy.

z_{0, x} = \frac{\int_{- t / 2}^{t / 2} E_{x}^{"} (z) z d z}{\int_{- t / 2}^{t / 2} E_{x}^{"} (z) d z} = \frac{I_{1}}{I_{0}}

Środek sztywności w x

D_{55, c a l c}^{"} = \frac{1}{\int_{- t / 2}^{t / 2} \frac{G_{11}^{"} (z)}{G_{11}^{"} (z) G_{22}^{"} (z) - {G_{12}^{"}}^{2} (z)} {(\frac{\int_{z}^{t / 2} E_{y}^{"} (\bar{z}) (\bar{z} - z_{0, x}) d \bar{z}}{\int_{- t / 2}^{t / 2} E_{y}^{"} (\bar{z}) {(\bar{z} - z_{0, x})}^{2} d \bar{z}})}^{2} d z}

Sztywność ścinania w kierunku y

Punkt sztywnościowy w kierunku y:

z_{0, x} = \frac{\int_{- t / 2}^{t / 2} E_{y}^{"} (z) z d z}{\int_{- t / 2}^{t / 2} E_{y}^{"} (z) d z} = \frac{I_{1}}{I_{0}}

Środek sztywności w kierunku y

Aby w obliczeniach sztywności ścinania uwzględnić orientację każdej warstwy, sztywności są określone według następujących równań.

G_{11, i}^{"} = \cos^{2} (φ - ß_{i}) G_{x z, i} + \sin^{2} (φ - ß_{i}) G_{y z, i}

Zorientowana sztywność na ścinanie G11

G tutaj oznacza sztywność ścinania warstw, aby uniknąć pomyłki z elementami macierzy sztywności (D).

Sztywność ścinania każdej warstwy można również przedstawić w formie macierzy w następujący sposób:

[\begin{matrix} G_{11} & G_{12} \\ G_{21} & G_{22} \end{matrix}]

Macierz sztywności na ścinanie

G_{22, i}^{"} = \sin^{2} (φ - ß_{i}) G_{x z, i} + \cos^{2} (φ - ß_{i}) G_{y z, i}

Zorientowana sztywność na ścinanie G22

Ewentualna ekscentryczność sztywności ścinania w poniższym równaniu dla wspomnianego symetrycznego układu płyty CLT (0°/90°/0°) zawsze byłaby zerowa i z tego powodu nieważna. Przy przykładowo ukośnie klejonym CLT (Diagonal Laminated Timber) ta część ekscentryczna jednak nie byłaby zerowa i dlatego grałaby ważną rolę.

G_{12}^{"} = (G_{x z, i} - G_{y z, i}) \sin (φ - ß_{i}) \cos (φ - ß_{i})

Sztywność na ścinanie mimośrodowe G12

Więcej informacji można znaleźć między innymi w [4] i w filmie na YouTube.

Obliczanie sztywności ścinania

Sztywność ścinania oblicza się w następujących krokach:

Najpierw określa się kąt maksymalnej sztywności. Kąt φ pokazuje zmianę lokalnego układu współrzędnych x powierzchni względem zorientowanego kierunku x''.
Wszystkie sztywności zgodnie z przedstawionymi powyżej równaniami są obracane w zorientowany kierunek x''.
Macierz sztywności dysku dla każdej warstwy (3 x 3) jest transformowana z lokalnego układu współrzędnych x', y' w obrócony system x'', y". Oprócz obliczania skierowanej sztywności ścinania każdej warstwy, jest to również wykonywane dla modułów sprężystości każdej warstwy.

$E_{x, i}^{"} = d_{12, i}^{"} + \frac{2 d_{12, i}^{"} d_{13, i}^{"} d_{23, i}^{"} - d_{22, i}^{"} {(d_{13, i}^{"})}^{2} - d_{33, i}^{"} {(d_{12, i}^{"})}^{2}}{d_{22, i}^{"} d_{33, i}^{"} - {(d_{23, i}^{"})}^{2}}$

Zorientowany moduł sprężystości w kierunku x

$E_{y, i}^{"} = d_{22, i}^{"} + \frac{2 d_{12, i}^{"} d_{13, i}^{"} d_{23, i}^{"} - d_{11, i}^{"} {(d_{23, i}^{"})}^{2} - d_{33, i}^{"} {(d_{12, i}^{"})}^{2}}{d_{11, i}^{"} d_{33, i}^{"} - {(d_{13, i}^{"})}^{2}}$

Zorientowany moduł sprężystości w kierunku y
Sztywność ścinania jest obliczana zgodnie z opisanymi powyżej równaniami (całka Grashoffa). Sztywność ścinania jest obliczana na podstawie poszczególnych składników.

$I = \int_{- h / 2}^{h / 2} d_{11} (z) {(z - z_{0, x})}^{2} d z = \sum_{i = 1}^{n} d_{11, i} \frac{{(z_{m a x, i} - z_{0, x})}^{3} - {(z_{m i n, i} - z_{0, x})}^{3}}{3}$

Moment bezwładności przekroju w kierunku x

$χ_{i} = d_{11, i} \frac{{(z_{m a x, i} - z_{0, x})}^{2}}{2} + \sum_{k = i + 1}^{n} d_{11, k} \frac{{(z_{m a x, i} - z_{0, x})}^{2} - {(z_{m i n, i} - z_{0, x})}^{2}}{2}$

Równoważna sztywność na warstwę (w x)

Tutaj równania pokazano tylko dla kierunku x (D44). Analogicznie do kierunku y. Równoważna sztywność (udział Steinerowski) jest obliczana dla każdej warstwy.
Obliczone sztywności dla zorientowanego kierunku całej konstrukcji są ostatecznie przeliczane zgodnie z relacjami kątowymi i uwzględniane jako oryginalne sztywności D44, D55 i D45 w macierzy sztywności.

$D_{44} = \cos^{2} (φ) D_{44}^{"} + \sin^{2} (φ) D_{55}^{"}$

Ponownie obliczona sztywność na ścinanie D44

$D_{55} = \sin^{2} (φ) D_{44}^{"} + \cos^{2} (φ) D_{55}^{"}$

Ponownie obliczona sztywność na ścinanie D55

$D_{45} = \sin (φ) \cos (φ) (D_{44}^{"} - D_{55}^{"})$

Ponownie obliczona sztywność na ścinanie D45

Zwiększenie sztywności ścinania

Ponieważ możliwe jest również modelowanie laminatów jako powierzchni w Geometrii z bardzo wąskimi pasami, należy przy obliczaniu takich problematycznych Geometrii odpowiednio zwiększyć sztywność ścinania.

W poniższym równaniu przedstawiono to dla kierunku X

D_{44}^{"} = \max (D_{44, calc}^{"}, \frac{48}{5 l ²} \frac{1}{\frac{1}{\sum_{i = 1}^{n} E_{x, i}^{"} \frac{t_{i}^{3}}{12}} - \frac{1}{\sum_{i = 1}^{n} E_{x, i}^{"} \frac{z_{\max, i}^{3} - z_{\min, i}^{3}}{3}}})

Maksymalna sztywność na ścinanie

Długość l w powyższym równaniu oznacza tutaj najkrótszą długość skrzynki, która może być umieszczona nad odpowiednią geometrią.

W dowolnym innym modelu, który można pobrać po prawej stronie, porównano wąską powierzchnię o szerokości 10 cm z identyczną powierzchnią o szerokości 20 cm.

Sztywność ścinania wąskiej powierzchni wynosi D44=15253 kN/m w porównaniu do D44=5970,8 kN/m dla szerszej powierzchni. W rezultacie, pomimo identycznego obciążenia, odkształcenie sztywniejszej powierzchni jest mniejsze, a siła ścinająca większa.

Sztywności w wielowarstwowych powierzchniach z zintegrowanymi objętościami

W przyszłości możliwe będzie w dodatku Powierzchnie wielowarstwowe definiowanie objętości razem z powierzchniami. Ten typ również eksportuje powierzchnię do RFEM. Ponieważ generowanie sztywności i rozdzielanie sił wewnętrznych jest bardziej skomplikowane, zostanie to omówione oddzielnie.

Odniesienia

Budownictwo z wykorzystaniem drewna klejonego krzyżowo. Nośne elementy z litego drewna na ściany, stropy i dachy - Seria 4 Część 6 Odcinek 1 Hamburger Informationsdienst Holz, Berlin, 2016
Płaskie konstrukcje powierzchniowe: Podstawy modelowania i obliczania tarcz i płyt
Jones, R. M. (b.d.). Mechanika materiałów kompozytowych (wyd. 2). Taylor & Francis Inc., Filadelfia.
Arnold, M.: "Właściwości mechaniczne drewna z warstwą krzyżową (DLT) w odniesieniu do stropów drewnianych podpartych punktowo". Rozprawa doktorska w trakcie opracowywania. Katedra Budownictwa Drewnianego i Budownictwa, Uniwersytet Techniczny w Monachium, oczekiwany w 2023 roku.

Rozdział nadrzędny

Teoria

Model

585x

23x

Modele wielowarstwowe

Model wielowarstwowy w usztywnieniu przy ścinaniu

70x

Sztywność na ścinanie