Manuels en ligne RFEM 6 | Surfaces multicouches

Retour aux manuels en ligne

2658x

003626

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

19.10.2023

Sélectionner le Manuel

Aperçu

Module complémentaire Surfaces multicouches

Théorie

Saisie

Résultats

Exemples de calcul

Rigidité pour des surfaces multicouches

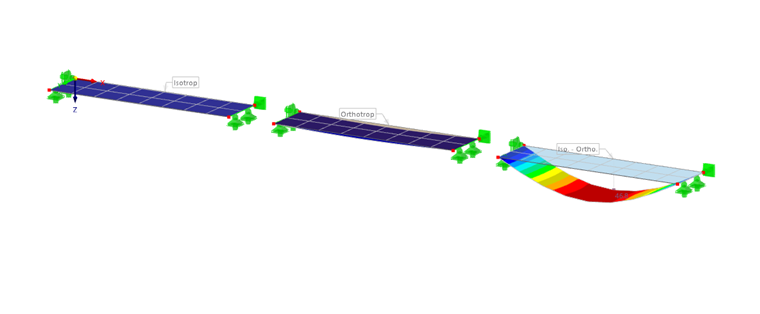
Modèles de matériaux

Les modèles de matériaux sont la base pour composer des surfaces multicouches en une rigidité de surface efficace. Avec le module complémentaire Surfaces multicouches, les modèles de matériaux peuvent être librement combinés dans le programme RFEM 6. Les principes des modèles de matériaux sont décrits dans les chapitres Matériaux et Comportement non linéaire du matériau du manuel de RFEM.

Une sélection des opitons de combinaisons des modèles de matériaux est configurée dans le modèle « Modèles multicouches » (voir colonne de droite), disponible au téléchargement pour étudier davantage les combinaisons.

La liste suivante montre une sélection de combinaisons possibles :

Couches isotropes (par ex. béton - acier)
Couches orthotropes (par ex. lamellé-croisé)
Isotrope - orthotrope (par ex. acier - PRV)
Isotrope Plastique - Isotrope (par ex. béton - acier)
Isotrope Non-linéaire Élastique - Orthotrope (par ex. béton - bois)
Isotrope - Orthotrope Plastique (par ex. béton - bois)
Isotrope endommagement - Orthotrope (par ex. béton - bois)

Informations

Pour combiner des matériaux non linéaires, le module complémentaire Comportement non linéaire du matériau doit être activé.

Rigidités des surfaces multicouches sans solide

La méthode de calcul la plus simple dans le module complémentaire Surfaces multicouches est de définir différentes couches de surface dans le type d’épaisseur « Couches » sans solide. Même ici, les modèles de matériaux peuvent être librement combinés.

Une fois les couches définies, le module complémentaire Surfaces multicouches génère une matrice de rigidité globale de la surface. Dans RFEM, les efforts internes et les déformations sont calculés pour cette surface. Dans le module complémentaire correspondant, tel que Vérification du bois ou Analyse contraintes-déformations, ces efforts internes sont ensuite distribués entre les couches présentes. En règle générale, les efforts internes sont affichés à trois points d’intégration par couche.

Processus de calcul pour surfaces multicouches

La suite explique le calcul de la matrice de rigidité pour un matériau isotrope et orthotrope.

Calcul de la matrice de rigidité

Les fondements des modèles de matériau observent les conditions suivantes (voir aussi le chapitre Matériaux du manuel de RFEM) :

Toutes les valeurs de rigidité ≥ 0
La matrice de rigidité globale de la surface doit être définie positive.
Équation fondamentale isotrope :

E = 2 G (1 + ν)

E	Module d’élasticité
G	Module de cisaillement
ν	Coefficient de Poisson

Module d’élasticité, module de cisaillement et coefficient de Poisson

Équation fondamentale orthotrope :

\frac{ν_{y x}}{E_{y}} = \frac{ν_{x y}}{E_{x}}

Relation de déformation transversale

Matrice de rigidité locale de chaque couche

Isotrope

d_{i}' = [\begin{matrix} d'_{11, i} & d'_{12, i} & 0 \\ d'_{22, i} & 0 \\ s y m . & d'_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{i}}{1 - ν_{i}^{2}} & \frac{ν_{i} E_{i}}{1 - ν_{i}^{2}} & 0 \\ \frac{E_{i}}{1 - ν_{i}^{2}} & 0 \\ s y m . & G_{i} \end{matrix}] i = 1, . . ., n m i t G_{i} = \frac{E_{i}}{2 (1 + ν_{i})}

Couche de matrice de rigidité isotrope

Orthotrope

d_{i}' = [\begin{matrix} d'_{11, i} & d'_{12, i} & 0 \\ d'_{22, i} & 0 \\ s y m . & d'_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{x, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & \frac{ν_{x y, i} E_{y, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ \frac{E_{y, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ s y m . & G_{x y, i} \end{matrix}] i = 1, . . ., n

Couche de matrice de rigidité orthotrope

Informations

Pour un matériau orthotrope, le module de cisaillement dans le plan de la plaque (G_xy) est défini par les valeurs du matériau, alors que pour un matériau isotrope, il est calculé à partir du module d’élasticité et du coefficient de Poisson. Par conséquent, pour un matériau orthotrope, la relation entre le coefficient de Poisson et le principe « lieu-cause » est importante.

Les rigidités en cisaillement pour un matériau orthotrope sont les suivantes :

G_xy	Module de cisaillement dans le plan de la plaque (par ex. 690 N/mm² pour C24)
G_xz	Module de cisaillement en direction x sur l’épaisseur (par ex. 690 N/mm² pour C24)
G_yz	Module de cisaillement en direction y sur l’épaisseur (par ex. 690 N/mm² pour C24) – également appelé « module de cisaillement roulant »

Pour un matériau orthotrope, il y a également la particularité que des rigidités dirigées peuvent être définies dans une surface. Dans le cas standard, l’orientation locale de la surface ou la couche en direction x correspond à la rigidité en direction x. Cependant, comme celle-ci peut être librement définie par l’angle β dans le type d’épaisseur « Couches », les rigidités doivent être transformées en conséquence.

d_{i} = [\begin{matrix} d_{11, i} & d_{12, i} & d_{13, i} \\ d_{22, i} & d_{23, i} \\ s y m . & d_{33, i} \end{matrix}] = T_{3 x 3, i}^{T} d'_{i} T_{3 x 3, i}

Rigidités de transformation

T_{3 x 3, i} = [\begin{matrix} c ² & s ² & c s \\ s ² & c ² & - c s \\ - 2 c s & 2 c s & c ² - s ² \end{matrix}] m i t c = \cos (β_{i}), s = \sin (β_{i})

Matrice de transformation

Somme de l'élément de chaque couche :

d_{11, i} = c^{4} d'_{11, i} + 2 c ² s ² d'_{12, i} + s^{4} d'_{22, i} + 4 c ² s ² d'_{33, i}

d_{12, i} = c^{2} s^{2} d'_{11, i} + s^{4} d'_{12, i} + c^{4} d'_{12, i} + c ² s ² d'_{22, i} - 4 c ² s ² d'_{33, i}

d_{13, i} = c^{3} s d'_{11, i} + c s^{3} d'_{12, i} - c^{3} s d'_{12, i} - c s^{3} d'_{22, i} - 2 c^{3} s d'_{33, i} + 2 c s^{3} d'_{33, i}

d_{22, i} = s^{4} d'_{11, i} + 2 c ² s ² d'_{12, i} + c^{4} d'_{22, i} + 4 c ² s ² d'_{33, i}

d_{23, i} = c s^{3} d'_{11, i} + c^{3} s d'_{12, i} - c s^{3} d'_{12, i} - c^{3} s d'_{22, i} + 2 c^{3} s d'_{33, i} - 2 c s^{3} d'_{33, i}

d_{33, i} = c^{2} s^{2} d'_{11, i} - 2 c ² s ² d'_{12, i} + c^{2} s^{2} d'_{22, i} + {(c^{2} - s^{2})}^{2} d'_{33, i}

Termes individuels par équipe

Éléments de flexion et de torsion [Nm]

Les éléments matriciels pour la flexion et la torsion sont donnés dans les équations suivantes.

D_{11} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{11, i}

Rigidité en flexion en x

D_{12} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{12, i}

Terme d'excentrement (12)

D_{22} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{22, i}

Rigidité en flexion en y

D_{13} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{13, i}

Terme d'excentrement (13)

D_{23} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{23, i}

Terme d'excentrement (23)

D_{33} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{33, i}

rigidité en torsion

Pour une seule couche dans le type d’épaisseur « Couches », le calcul est effectué en utilisant les équations détaillées dans le manuel de RFEM.

Pour le cisaillement (éléments D44/55), différentes équations s’appliquent dans le type d'épaisseur « Couches ». Elles sont présentées dans Cisaillement dans le plan des plaques.

Termes d’excentrement [Nm/m]

Les termes d’excentrement apparaissent pour des plaques asymétriques. Une surface asymétrique peut, par exemple, résulter de carbonisation sur un seul côté d’une plaque en CLT dans la vérification de la résistance au feu. Les éléments matriciels sont les suivants :

D_{16} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{11, i}

Élément d'excentrement D16

D_{17} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{12, i}

Élément d'excentrement D17

D_{18} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{13, i}

Élément d'excentrement D18

D_{27} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{22, i}

Élément d'excentrement D27

D_{28} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{23, i}

Élément d'excentrement D28

D_{38} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{33, i}

Élément d'excentrement D38

Plan de la plaque [N/m]

Pour le plan de la plaque, les rigidités normales sont traitées dans ce plan. Avec l’élément D88, le cisaillement dans le plan de la plaque – donc l’effort tranchant dans la plaque – est calculé. Les éléments matriciels sont les suivants :

D_{66} = \sum_{i = 1}^{n} t_{i} d_{11, i}

Rigidité axiale x D66

D_{67} = \sum_{i = 1}^{n} t_{i} d_{12, i}

Rigidité normale Excentrique D67

D_{68} = \sum_{i = 1}^{n} t_{i} d_{13, i}

Rigidité normale Excentrique D68

D_{77} = \sum_{i = 1}^{n} t_{i} d_{22, i}

Rigidité axiale y D77

D_{78} = \sum_{i = 1}^{n} t_{i} d_{23, i}

Rigidité normale Excentrique D78

D_{88} = \sum_{i = 1}^{n} t_{i} d_{33, i}

Cisaillement de plaque D88

Cisaillement dans le plan des plaques [N/m]

Pour déterminer la rigidité en cisaillement, la direction des rigidités d’un matériau orthotrope doit être adaptée par rapport à l’axe local de la surface. Cela doit être fait pour chaque couche du type d’épaisseur « Couches ». Avec une construction simple où la couche extérieure est orientée à 0° et la couche intérieure à 90°, il en résulte une grande flexibilité en cisaillement, ce qui doit être pris en compte dans le modèle multicouches. L’image suivante, issue de l’exemple d'une plaque en bois lamellé-croisé, le montre (source [1]).

Illustration d’une déformation de cisaillement dans le bois lamellé-croisé, fournie par le service d'information sur le bois

Déformation due au cisaillement (Source : Informationsdienst Holz)

Dans la théorie des stratifiés, la rigidité en cisaillement d’une structure stratifiée est calculée par la transformation de toutes les composantes de flexion et de cisaillement dans les directions respectives de chaque couche. Pour en savoir plus, consultez la littérature citée ci-dessous.

Visualisation de l’orientation des axes de rigidité dans un matériau stratifié pour optimiser les propriétés du matériau.

Orientation de raideur

Avec la transformation de la rigidité illustrée dans l’image, les rigidités sont additionnées. Cette addition est également connue sous le nom d’intégrale de Grashoff.

D_{44, c a l c}^{"} = \frac{1}{\int_{- t / 2}^{t / 2} \frac{G_{22}^{"} (z)}{G_{11}^{"} (z) G_{22}^{"} (z) - {G_{12}^{"}}^{2} (z)} {(\frac{\int_{z}^{t / 2} E_{x}^{"} (\bar{z}) (\bar{z} - z_{0, x}) d \bar{z}}{\int_{- t / 2}^{t / 2} E_{x}^{"} (\bar{z}) {(\bar{z} - z_{0, x})}^{2} d \bar{z}})}^{2} d z}

Rigidité de cisaillement dans la direction x

Pour le calcul de la rigidité en x et y, un centre de rigidité est déterminé pour chaque structure d’une surface multicouche.

z_{0, x} = \frac{\int_{- t / 2}^{t / 2} E_{x}^{"} (z) z d z}{\int_{- t / 2}^{t / 2} E_{x}^{"} (z) d z} = \frac{I_{1}}{I_{0}}

Centre de rigidité en x

D_{55, c a l c}^{"} = \frac{1}{\int_{- t / 2}^{t / 2} \frac{G_{11}^{"} (z)}{G_{11}^{"} (z) G_{22}^{"} (z) - {G_{12}^{"}}^{2} (z)} {(\frac{\int_{z}^{t / 2} E_{y}^{"} (\bar{z}) (\bar{z} - z_{0, x}) d \bar{z}}{\int_{- t / 2}^{t / 2} E_{y}^{"} (\bar{z}) {(\bar{z} - z_{0, x})}^{2} d \bar{z}})}^{2} d z}

Rigidité de cisaillement en direction de l'axe y

Centre de rigidité en direction y :

z_{0, x} = \frac{\int_{- t / 2}^{t / 2} E_{y}^{"} (z) z d z}{\int_{- t / 2}^{t / 2} E_{y}^{"} (z) d z} = \frac{I_{1}}{I_{0}}

Centre de rigidité dans la direction y

Pour la prise en compte de l’orientation par couche dans le calcul de la rigidité au cisaillement, les rigidités sont déterminées selon les équations suivantes.

G_{11, i}^{"} = \cos^{2} (φ - ß_{i}) G_{x z, i} + \sin^{2} (φ - ß_{i}) G_{y z, i}

Rigidité de cisaillement orientée G11

G représente ici la rigidité en cisaillement des couches, afin d’éviter toute confusion avec les éléments de la matrice de rigidité (D).

La rigidité en cisaillement de chaque couche peut également être présentée sous forme matricielle comme suit :

[\begin{matrix} G_{11} & G_{12} \\ G_{21} & G_{22} \end{matrix}]

Matrice de rigidité en cisaillement

G_{22, i}^{"} = \sin^{2} (φ - ß_{i}) G_{x z, i} + \cos^{2} (φ - ß_{i}) G_{y z, i}

Rigidité de cisaillement orientée G22

La rigidité en cisaillement excentrée dans l’équation suivante serait toujours nulle pour la construction symétrique mentionnée au début d’une plaque en bois lamellé-croisé (0°/90°/0°) et n’est donc pas pertinente. Pour un matériau CLT collé en diagonale (« Diagonal Laminated Timber »), cependant, ce terme d’excentrement n’est pas nul et joue donc un rôle important.

G_{12}^{"} = (G_{x z, i} - G_{y z, i}) \sin (φ - ß_{i}) \cos (φ - ß_{i})

Rigidité de cisaillement orienté excentrement G12

Vous trouverez de plus amples informations dans la référence [4] et dans une vidéo YouTube.

Calcul de la rigidité en cisaillement

La rigidité en cisaillement est déterminée selon les étapes suivantes :

D'abord, l’angle de la rigidité maximale est déterminé. L’angle φ montre le changement du système de coordonnées local x de la surface par rapport à la direction orientée x’’.
Toutes les rigidités sont tournées selon les équations présentées ci-dessus dans la direction orientée x’’.
La matrice de rigidité de chaque couche (3 x 3) est transformée du système de coordonnées local x’, y’ vers le système pivoté x’’, y’’. En plus du calcul de la rigidité en cisaillement dirigée de chaque couche, cela est également réalisé pour les modules d’élasticité de chaque couche.

E_{x, i}^{"} = d_{12, i}^{"} + \frac{2 d_{12, i}^{"} d_{13, i}^{"} d_{23, i}^{"} - d_{22, i}^{"} {(d_{13, i}^{"})}^{2} - d_{33, i}^{"} {(d_{12, i}^{"})}^{2}}{d_{22, i}^{"} d_{33, i}^{"} - {(d_{23, i}^{"})}^{2}}

Module d'élasticité orienté dans la direction x

E_{y, i}^{"} = d_{22, i}^{"} + \frac{2 d_{12, i}^{"} d_{13, i}^{"} d_{23, i}^{"} - d_{11, i}^{"} {(d_{23, i}^{"})}^{2} - d_{33, i}^{"} {(d_{12, i}^{"})}^{2}}{d_{11, i}^{"} d_{33, i}^{"} - {(d_{13, i}^{"})}^{2}}

Module d'élasticité orienté dans la direction y

La rigidité en cisaillement est calculée avec les équations décrites ci-dessus (Intégrale de Grashoff).

La rigidité en cisaillement est calculée selon les composantes individuelles.

I = \int_{- h / 2}^{h / 2} d_{11} (z) {(z - z_{0, x})}^{2} d z = \sum_{i = 1}^{n} d_{11, i} \frac{{(z_{m a x, i} - z_{0, x})}^{3} - {(z_{m i n, i} - z_{0, x})}^{3}}{3}

Moment d'inertie dans la direction x

χ_{i} = d_{11, i} \frac{{(z_{m a x, i} - z_{0, x})}^{2}}{2} + \sum_{k = i + 1}^{n} d_{11, k} \frac{{(z_{m a x, i} - z_{0, x})}^{2} - {(z_{m i n, i} - z_{0, x})}^{2}}{2}

Rigidité équivalente par couche (en x)

Ici, les équations sont seulement montrées pour la direction x (D44). Pour la direction y, cela s’applique de manière similaire.
La rigidité équivalente (terme de Steiner) est calculée pour chaque couche.

Les rigidités calculées pour la direction orientée d’une construction complète sont finalement calculées rétroactivement à partir des relations angulaires et affichées comme rigidités originaires D44, D55 et D45 dans la matrice de rigidité.

D_{44} = \cos^{2} (φ) D_{44}^{"} + \sin^{2} (φ) D_{55}^{"}

Rigidité de cisaillement D44 recalculée

D_{55} = \sin^{2} (φ) D_{44}^{"} + \cos^{2} (φ) D_{55}^{"}

Rigidité de cisaillement D55 recalculée

D_{45} = \sin (φ) \cos (φ) (D_{44}^{"} - D_{55}^{"})

Rigidité de cisaillement D45 recalculée

Augmentation de la rigidité en cisaillement

Étant donné que la modélisation des stratifiés comme surface rend possible des géométries avec des bandes de surface très étroites, la rigidité en cisaillement doit être augmentée de manière appropriée pour ces géométries problématiques dans le calcul.

L’équation suivante illustre cela pour la direction X

D_{44}^{"} = \max (D_{44, calc}^{"}, \frac{48}{5 l ²} \frac{1}{\frac{1}{\sum_{i = 1}^{n} E_{x, i}^{"} \frac{t_{i}^{3}}{12}} - \frac{1}{\sum_{i = 1}^{n} E_{x, i}^{"} \frac{z_{\max, i}^{3} - z_{\min, i}^{3}}{3}}})

Rigidité maximale de cisaillement

La longueur l dans l’équation ci-dessus signifie ici la plus courte longueur d’une boîte qui peut être placée sur la géométrie correspondante.

Dans un autre modèle, disponible au téléchargement à droite, une surface étroite d’une largeur de 10 cm a été comparée avec une surface identique de 20 cm.

La rigidité en cisaillement de la surface étroite est D44=15253kN/m par rapport à D44=5970.8kN/m pour la surface plus large. En conséquence, malgré une charge identique, la déformation de la surface la plus rigide est inférieure et la charge de cisaillement est plus élevée.

Rigidités des surfaces multicouches avec solides intégrés

À l'avenir, le module complémentaire Surfaces multicouches de définir des soldies en conjonction avec des surfaces. Avec ce type, une surface est également exportée vers RFEM. Étant donné que la génération des rigidités et la décomposition des efforts internes sont plus complexes, une explication séparée sera fournie.

Références

Construction en bois lamellé-croisé. Éléments porteurs en bois massif pour les murs, planchers et toitures - Série 4 Partie 6 Épisode 1. Service d’information sur le bois, Berlin, 2016
Structures planes : Bases de la modélisation et du calcul des voiles et plaques
Jones, R. M. (n.d.). Mechanics of Composite Materials (2nde éd.). Taylor & Francis Inc., Philadelphie.
Arnold, M. : « Propriétés mécaniques du bois contrecollé diagonal (DLT) en rapport avec les dalles en bois massif à appui ponctuel ». Thèse de doctorat en cours. Chaire de constructions bois et de structures, Université technique de Munich, 2023.

Chapitre parent

Théorie

Modèle

640x

24x

Modèles multicouches

Modèle multicouche dans un raidisseur de cisaillement

86x

Rigidité en cisaillement