Manuali online RFEM 6 | Superfici multistrato

Torna a Manuali online

2263x

003626

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

2023-10-19

Seleziona il manuale

Panoramica

Add-on di superfici multistrato

Metodo di analisi

Input

Risultati

Esempi di calcolo

Rigidezze per superfici multistrato

Modelli di materiale

La base per la composizione di superfici multistrato in una rigidezza superficiale efficace sono i modelli di materiale. Con l'Add-On Superfici Multistrato, i modelli di materiale possono essere liberamente combinati nel programma RFEM 6. Le basi dei modelli di materiale sono descritte nei capitoli Materiali e Comportamento Materiale Non Lineare del manuale RFEM.

Una selezione delle combinazioni possibili dei modelli di materiale è impostata nel modello "Modelli Multistrato" (vedere colonna a destra), che si può scaricare per ulteriori studi sulle combinazioni.

Il seguente elenco mostra una selezione delle possibili combinazioni:

Strati isotropi (ad es. cemento - acciaio)
Strati ortotropi (ad es. legno lamellare incrociato)
Isotropo - ortotropo (ad es. acciaio - GFK)
Isotropa Plastica - Isotropa (ad es. cemento - acciaio)
Isotropo Non Lineare Elastico - Ortotropo (ad es. cemento - legno)
Isotropo - Ortotropo Plastico (ad es. cemento - legno)
Isotropo Danneggiamento - Ortotropo (ad es. cemento - legno)

Informazione

Per la combinazione di materiali non lineari deve essere attivato l'Add-On Comportamento Materiale Non Lineare.

Rigidità delle superfici multistrato senza volume

La variante di calcolo più semplice nell'Add-On Superfici Multistrato è quella di definire diversi strati superficiali nel tipo di spessore 'Strati' senza volume. Anche qui, tuttavia, i modelli di materiale possono essere liberamente combinati.

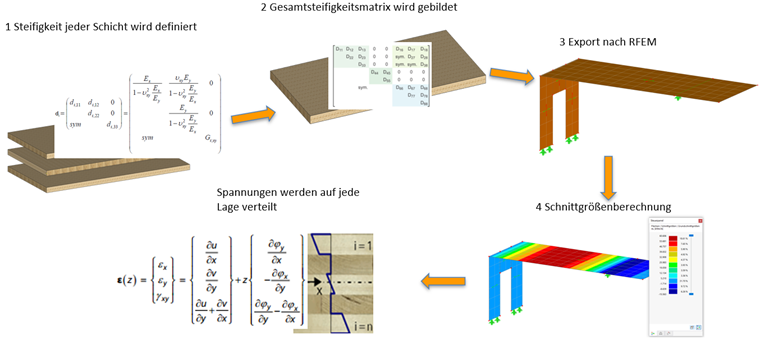
Una volta definiti gli strati, l'Add-On Superfici Multistrato genera una matrice globale di rigidezza della superficie. In RFEM sono calcolati per questa superficie le grandezze interne e le deformazioni. Nell'Add-On di verifica come calcolo del legno o calcolo delle tensioni-deformazioni, queste grandezze interne sono quindi suddivise negli strati presenti. Di solito, le grandezze interne sono indicate su tre punti di integrazione per stato.

Processo di calcolo per superfici multistrato

Nel seguito, viene spiegato il calcolo della matrice di rigidità per materiali isotropi e ortotropi.

Calcolo della matrice di rigidità

Come basi dei modelli di materiale valgono le seguenti condizioni (vedi anche il capitolo Materiali del manuale RFEM):

Tutti i valori di rigidità devono essere ≥ 0
La matrice di rigidità complessiva della superficie deve essere definita positiva.
Equazione base Isotropo:

E = 2 G (1 + ν)

E	Modulo E
G	Modulo di taglio
ν	deformazione trasversale

Modulo di elasticità, modulo di taglio e coefficiente di Poisson's

Equazione base Ortotropo:

\frac{ν_{y x}}{E_{y}} = \frac{ν_{x y}}{E_{x}}

Relazione di deformazione trasversale

Matrice di rigidità locale di ogni strato

Isotropo

d_{i}' = [\begin{matrix} d'_{11, i} & d'_{12, i} & 0 \\ d'_{22, i} & 0 \\ s y m . & d'_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{i}}{1 - ν_{i}^{2}} & \frac{ν_{i} E_{i}}{1 - ν_{i}^{2}} & 0 \\ \frac{E_{i}}{1 - ν_{i}^{2}} & 0 \\ s y m . & G_{i} \end{matrix}] i = 1, . . ., n m i t G_{i} = \frac{E_{i}}{2 (1 + ν_{i})}

Strato della matrice di rigidezza isotropo

Ortotropo

d_{i}' = [\begin{matrix} d'_{11, i} & d'_{12, i} & 0 \\ d'_{22, i} & 0 \\ s y m . & d'_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{x, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & \frac{ν_{x y, i} E_{y, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ \frac{E_{y, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ s y m . & G_{x y, i} \end{matrix}] i = 1, . . ., n

Strato della matrice di rigidezza ortotropo

Informazione

Nel materiale ortotropo il modulo di taglio nel piano della lamina (G_xy) è definito attraverso i valori del materiale, mentre nel materiale isotropo è determinato dal modulo di elasticità e dal coefficiente di Poisson. Questo è il motivo per cui, nel materiale ortotropo, la relazione di deformazione trasversale secondo il principio "luogo-causa" è importante.

Le rigidezze di taglio per materiale ortotropo sono le seguenti:

G_xy	Modulo di taglio nel piano della lamina (ad es. 690 N/mm² per C24)
G_xz	Modulo di taglio nella direzione x attraverso lo spessore (ad es. 690 N/mm² per C24)
G_yz	Modulo di taglio nella direzione y attraverso lo spessore (ad es. 690 N/mm² per C24) – anche chiamato "modulo di taglio a rotazione"

Nel materiale ortotropo si ha anche la particolarità che le rigidità direzionali possono essere definite su una superficie. Nel caso standard, l'orientamento locale della superficie o dello strato nella direzione x corrisponde alla rigidezza nella direzione x. Tuttavia, poiché può essere definito liberamente tramite l'angolo β nel tipo di spessore 'Strati', è necessario trasformare le rigidezze di conseguenza.

d_{i} = [\begin{matrix} d_{11, i} & d_{12, i} & d_{13, i} \\ d_{22, i} & d_{23, i} \\ s y m . & d_{33, i} \end{matrix}] = T_{3 x 3, i}^{T} d'_{i} T_{3 x 3, i}

Rigidezze di trasformazione

T_{3 x 3, i} = [\begin{matrix} c ² & s ² & c s \\ s ² & c ² & - c s \\ - 2 c s & 2 c s & c ² - s ² \end{matrix}] m i t c = \cos (β_{i}), s = \sin (β_{i})

Matrice di trasformazione

Somma degli elementi di ogni strato:

d_{11, i} = c^{4} d'_{11, i} + 2 c ² s ² d'_{12, i} + s^{4} d'_{22, i} + 4 c ² s ² d'_{33, i}

d_{12, i} = c^{2} s^{2} d'_{11, i} + s^{4} d'_{12, i} + c^{4} d'_{12, i} + c ² s ² d'_{22, i} - 4 c ² s ² d'_{33, i}

d_{13, i} = c^{3} s d'_{11, i} + c s^{3} d'_{12, i} - c^{3} s d'_{12, i} - c s^{3} d'_{22, i} - 2 c^{3} s d'_{33, i} + 2 c s^{3} d'_{33, i}

d_{22, i} = s^{4} d'_{11, i} + 2 c ² s ² d'_{12, i} + c^{4} d'_{22, i} + 4 c ² s ² d'_{33, i}

d_{23, i} = c s^{3} d'_{11, i} + c^{3} s d'_{12, i} - c s^{3} d'_{12, i} - c^{3} s d'_{22, i} + 2 c^{3} s d'_{33, i} - 2 c s^{3} d'_{33, i}

d_{33, i} = c^{2} s^{2} d'_{11, i} - 2 c ² s ² d'_{12, i} + c^{2} s^{2} d'_{22, i} + {(c^{2} - s^{2})}^{2} d'_{33, i}

Singoli termini per turno

Elementi di flessione e torsione [Nm]

Gli elementi della matrice per la flessione e la torsione sono indicati nelle seguenti equazioni.

D_{11} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{11, i}

Rigidezza flessionale in x

D_{12} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{12, i}

Termine eccentrico (12)

D_{22} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{22, i}

Rigidezza flessionale in y

D_{13} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{13, i}

Termine eccentrico (13)

D_{23} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{23, i}

Termine eccentrico (23)

D_{33} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{33, i}

rigidezza torsionale

Con solo uno strato nel tipo di spessore 'Strati', il calcolo viene fatto secondo le equazioni spiegate nel manuale RFEM.

Per il taglio (elementi D44/55), nel tipo di spessore 'Strati' sono valide altre equazioni. Queste vengono presentate nella sezione Taglio nel piano della lastra.

Termini di eccentricità [Nm/m]

In piastre asimmetriche risultano termini di eccentricità. Una superficie asimmetrica può, ad esempio, verificarsi nella verifica antincendio per una piastra in legno lamellare incrociato che brucia da un lato. Gli elementi della matrice sono come segue:

D_{16} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{11, i}

Elemento di eccentricità D16

D_{17} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{12, i}

Elemento di eccentricità D17

D_{18} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{13, i}

Elemento di eccentricità D18

D_{27} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{22, i}

Elemento di eccentricità D27

D_{28} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{23, i}

Elemento di eccentricità D28

D_{38} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{33, i}

Elemento di eccentricità D38

Piano della lastra [N/m]

Nel piano della lastra vengono trattate le rigidità normali nel piano della lastra. Con l'elemento D88 si calcola il taglio della lastra, ovvero lo sforzo trasversale nella lastra. Gli elementi della matrice sono come segue:

D_{66} = \sum_{i = 1}^{n} t_{i} d_{11, i}

Rigidezza assiale x D66

D_{67} = \sum_{i = 1}^{n} t_{i} d_{12, i}

Rigidezza normale Eccentrico D67

D_{68} = \sum_{i = 1}^{n} t_{i} d_{13, i}

Rigidezza normale Eccentrico D68

D_{77} = \sum_{i = 1}^{n} t_{i} d_{22, i}

Rigidezza assiale y D77

D_{78} = \sum_{i = 1}^{n} t_{i} d_{23, i}

Rigidezza normale Eccentrico D78

D_{88} = \sum_{i = 1}^{n} t_{i} d_{33, i}

Taglio della piastra D88

Taglio nel piano della lastra [N/m]

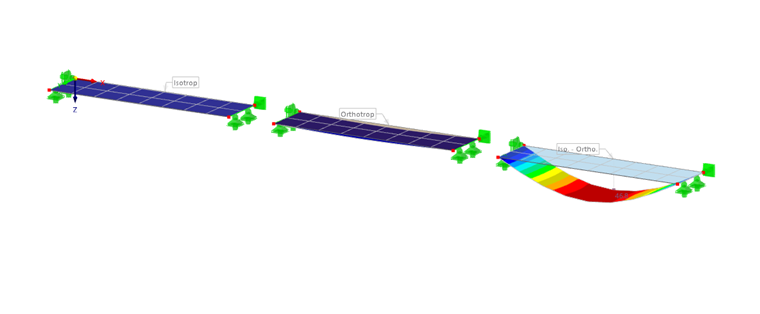
Per determinare la rigidezza tagliante, in un materiale ortotropo, le rigidità devono essere ruotate rispetto al loro orientamento rispetto all'asse locale della superficie. Questo deve essere fatto per ogni posizione del tipo di spessore 'Strati'. Con una struttura semplice degli strati con orientamento della superficie di copertura di 0° e dell'altro strato di 90°, si ottiene una grande cedevolezza al taglio, che deve essere presa in considerazione nel modello multistrato. Nell'immagine seguente (fonte [1]) questo è evidente nell'esempio di una piastra in legno lamellare incrociato.

Illustrazione della deformazione da taglio del CLT | Infołan

Deformazione da taglio (fonte: wood.de)

Nella teoria del laminato, la rigidezza tagliante di una struttura a strati è calcolata attraverso la trasformazione di tutte le componenti di piega e taglio nelle rispettive direzioni di ciascuno strato. Ulteriori informazioni si possono trovare anche nella letteratura sotto elencata.

Visualizzazione dell'orientamento degli assi di rigidezza in un laminato per ottimizzare le proprietà del materiale.

Orientamento della rigidezza

Attraverso la trasformazione della rigidezza mostrata nell'immagine, le rigidezze vengono sommate. Questa somma è nota anche come "Integrale di Grashoff".

D_{44, c a l c}^{"} = \frac{1}{\int_{- t / 2}^{t / 2} \frac{G_{22}^{"} (z)}{G_{11}^{"} (z) G_{22}^{"} (z) - {G_{12}^{"}}^{2} (z)} {(\frac{\int_{z}^{t / 2} E_{x}^{"} (\bar{z}) (\bar{z} - z_{0, x}) d \bar{z}}{\int_{- t / 2}^{t / 2} E_{x}^{"} (\bar{z}) {(\bar{z} - z_{0, x})}^{2} d \bar{z}})}^{2} d z}

Rigidezza a taglio in direzione x

Per il calcolo della rigidità nelle direzioni x e y, viene calcolato il cosiddetto punto centrale di rigidezza per ogni configurazione di una superficie multistrato.

z_{0, x} = \frac{\int_{- t / 2}^{t / 2} E_{x}^{"} (z) z d z}{\int_{- t / 2}^{t / 2} E_{x}^{"} (z) d z} = \frac{I_{1}}{I_{0}}

Centro di rigidezza in x

D_{55, c a l c}^{"} = \frac{1}{\int_{- t / 2}^{t / 2} \frac{G_{11}^{"} (z)}{G_{11}^{"} (z) G_{22}^{"} (z) - {G_{12}^{"}}^{2} (z)} {(\frac{\int_{z}^{t / 2} E_{y}^{"} (\bar{z}) (\bar{z} - z_{0, x}) d \bar{z}}{\int_{- t / 2}^{t / 2} E_{y}^{"} (\bar{z}) {(\bar{z} - z_{0, x})}^{2} d \bar{z}})}^{2} d z}

Rigidezza a taglio in direzione y

Punto centrale di rigidezza nella direzione y:

z_{0, x} = \frac{\int_{- t / 2}^{t / 2} E_{y}^{"} (z) z d z}{\int_{- t / 2}^{t / 2} E_{y}^{"} (z) d z} = \frac{I_{1}}{I_{0}}

Centro di rigidezza in direzione y

Per catturare l'orientamento per ogni strato nel calcolo della rigidezza tagliante, le rigidità sono registrate secondo le seguenti equazioni.

G_{11, i}^{"} = \cos^{2} (φ - ß_{i}) G_{x z, i} + \sin^{2} (φ - ß_{i}) G_{y z, i}

Rigidezza a taglio orientata G11

G rappresenta la rigidezza tagliante degli strati, per evitare confusione con gli elementi della matrice di rigidezza (D).

Anche la rigidezza tagliante di ciascun strato può essere rappresentata come segue in forma di matrice:

[\begin{matrix} G_{11} & G_{12} \\ G_{21} & G_{22} \end{matrix}]

Matrice di rigidezza a taglio

G_{22, i}^{"} = \sin^{2} (φ - ß_{i}) G_{x z, i} + \cos^{2} (φ - ß_{i}) G_{y z, i}

Rigidezza a taglio orientata G22

La rigidità tagliante eccentrica nella seguente equazione risulterebbe sempre nulla nel caso menzionato inizialmente di una configurazione simmetrica di legno lamellare incrociato (0°/90°/0°) e quindi non rilevante. Tuttavia, in un legno lamellare incrociato DLT (Diagonal Laminated Timber) incollato diagonalmente, questo termine di eccentricità non è nullo e gioca quindi un ruolo importante.

G_{12}^{"} = (G_{x z, i} - G_{y z, i}) \sin (φ - ß_{i}) \cos (φ - ß_{i})

Rigidezza a taglio eccentrico orientato G12

Altre informazioni si possono trovare ad esempio in [4] e in un video su YouTube.

Calcolo della rigidezza tagliante

La rigidezza tagliante viene determinata con i seguenti passaggi:

In primo luogo, viene determinato l'angolo di massima rigidezza. L'angolo φ mostra la modifica del sistema di coordinate locale x della superficie in direzione x''.
Tutte le rigidezze vengono ruotate nella direzione orientata x'' secondo le equazioni sopra presentate.
La matrice di rigidezza della lastra di ogni strato (3 x 3) viene trasformata dal sistema di coordinate locale x', y' nel sistema ruotato x'', y" . Oltre al calcolo della rigidezza diretta di ogni singolo strato, ciò viene fatto anche per i moduli di elasticità di ogni strato.

$E_{x, i}^{"} = d_{12, i}^{"} + \frac{2 d_{12, i}^{"} d_{13, i}^{"} d_{23, i}^{"} - d_{22, i}^{"} {(d_{13, i}^{"})}^{2} - d_{33, i}^{"} {(d_{12, i}^{"})}^{2}}{d_{22, i}^{"} d_{33, i}^{"} - {(d_{23, i}^{"})}^{2}}$

Modulo di elasticità orientato in direzione x

$E_{y, i}^{"} = d_{22, i}^{"} + \frac{2 d_{12, i}^{"} d_{13, i}^{"} d_{23, i}^{"} - d_{11, i}^{"} {(d_{23, i}^{"})}^{2} - d_{33, i}^{"} {(d_{12, i}^{"})}^{2}}{d_{11, i}^{"} d_{33, i}^{"} - {(d_{13, i}^{"})}^{2}}$

Modulo di elasticità orientato in direzione y
La rigidezza tagliante viene calcolata con le equazioni sopra descritte (Integrale di Grashoff). La rigidezza tagliante viene calcolata con le singole componenti.

$I = \int_{- h / 2}^{h / 2} d_{11} (z) {(z - z_{0, x})}^{2} d z = \sum_{i = 1}^{n} d_{11, i} \frac{{(z_{m a x, i} - z_{0, x})}^{3} - {(z_{m i n, i} - z_{0, x})}^{3}}{3}$

Secondo momento dell'area in direzione x

$χ_{i} = d_{11, i} \frac{{(z_{m a x, i} - z_{0, x})}^{2}}{2} + \sum_{k = i + 1}^{n} d_{11, k} \frac{{(z_{m a x, i} - z_{0, x})}^{2} - {(z_{m i n, i} - z_{0, x})}^{2}}{2}$

Rigidezza equivalente per strato (in x)

Qui le equazioni sono mostrate solo per la direzione x (D44). Questo vale analogamente per la direzione y. La rigidezza equivalente (termine di Steiner) viene calcolato per ogni strato.
Le rigidezze calcolate per la direzione orientata di una struttura complessiva vengono infine riconvertite attraverso le relazioni angolari e riportate come rigidezze originarie D44, D55 e D45 nella matrice di rigidezza.

$D_{44} = \cos^{2} (φ) D_{44}^{"} + \sin^{2} (φ) D_{55}^{"}$

Rigidezza a taglio ricalcolata D44

$D_{55} = \sin^{2} (φ) D_{44}^{"} + \cos^{2} (φ) D_{55}^{"}$

Rigidezza a taglio ricalcolata D55

$D_{45} = \sin (φ) \cos (φ) (D_{44}^{"} - D_{55}^{"})$

Rigidezza a taglio ricalcolata D45

Incremento della rigidezza tagliante

Poiché attraverso una modellazione di laminati come superficie sono possibili anche geometrie con superfici molto strette, nella simulazione di tali geometrie problematiche la rigidezza tagliante deve essere ampliata di conseguenza.

Seguente equazione mostra questo nella direzione X

D_{44}^{"} = \max (D_{44, calc}^{"}, \frac{48}{5 l ²} \frac{1}{\frac{1}{\sum_{i = 1}^{n} E_{x, i}^{"} \frac{t_{i}^{3}}{12}} - \frac{1}{\sum_{i = 1}^{n} E_{x, i}^{"} \frac{z_{\max, i}^{3} - z_{\min, i}^{3}}{3}}})

Massima rigidezza a taglio

La lunghezza l nella suddetta equazione rappresenta qui la lunghezza minima di una scatola che può essere posata sulla rispettiva geometria.

In un ulteriore modello, che può essere scaricato a destra, è stata confrontata una superficie sottile di larghezza con un'identica superficie larga 20 cm.

La rigidezza tagliante della superficie sottile è D44=15253kN/m rispetto a D44=5970,8kN/m della superficie più larga. Di conseguenza, nonostante il carico identico la deformazione della superficie più rigida è minore e il carico di taglio maggiore.

Rigidità delle superfici multistrato con volume integrato

In futuro, sarà possibile anche nell'Add-On Superfici Multistrato definire volumi insieme a superfici. Anche in questo tipo, una superficie sarà esportata in RFEM. Poiché la generazione delle rigidezze e la scomposizione delle grandezze interne è più complessa, questo verrà spiegato separatamente.

Bibliografia

Costruire con XLAM
Elementi telaio in legno massiccio per pareti, solai e coperture - Parte 4, Parte 6, Episodio 1. Servizio Informazione sul legno, Berlino, 2016
Strutture di superficie piane: Principi di modellazione e analisi di pareti e piastre
Jones, R. M. (n.d.). Mechanics of Composite Materials (2a ed.). Taylor & Francis Inc., Philadelphia.
Arnold, M.:Mechanical Properties of Diagonal Laminated Timber (DLT) with respect to point-supported mass timber slabs.Tesi in sviluppo. Dipartimento di Ingegneria del Legno e delle Costruzioni, Technische Universität München, prevista per il 2023.

Capitolo principale

Metodo di analisi

Modello

585x

23x

Modelli multistrato

Modello multistrato con irrigidimento a taglio

70x

rigidezza a taglio