Manuales en línea RFEM 6 | Superficies multicapa

Volver a manuales en línea

2263x

003626

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

19-10-2023

Seleccionar manual

Visión de conjunto

Complemento Superficies multicapa

Teoría

Entrada de datos

Resultados

Ejemplos de cálculo

Rigideces para superficies multicapa

Modelos de material

La base para la composición de superficies multicapa hacia una rigidez efectiva de la superficie son los modelos de material. Con el complemento para superficies multicapa, los modelos de material pueden combinarse libremente en el programa RFEM 6. Las bases de los modelos de material se describen en los capítulos Materiales y Comportamiento no lineal del material del manual de RFEM.

Una selección de las posibilidades de combinación de los modelos de material está dispuesta en el modelo "Modelos multicapa" (ver columna derecha), que se puede descargar para un estudio adicional de las combinaciones.

La siguiente lista muestra una selección de combinaciones posibles:

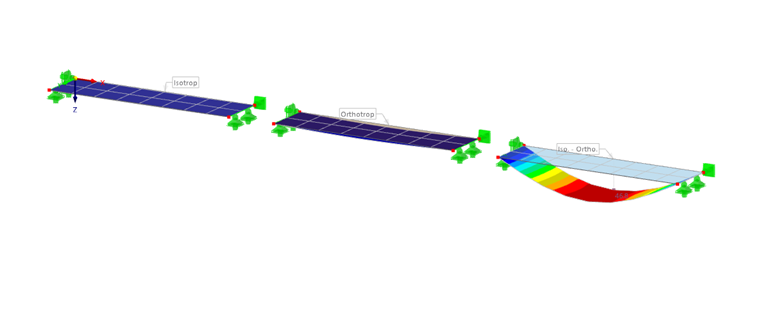
Capas isotrópicas (por ejemplo, hormigón - acero)
Capas ortotrópicas (por ejemplo, madera contralaminada)
Isotrópico - ortotrópico (por ejemplo, acero - GFRP)
Isotrópico plástico - isotrópico (por ejemplo, hormigón - acero)
Isotrópico no lineal elástico - ortotrópico (por ejemplo, hormigón - madera)
Isotrópico - ortotrópico plástico (por ejemplo, hormigón - madera)
Isotrópico con daño - ortotrópico (por ejemplo, hormigón - madera)

Información

Para la combinación de materiales no lineales, debe estar activado el complemento Comportamiento no lineal del material.

Rigideces en superficies multicapa sin volumen

La variante de cálculo más sencilla en el complemento para superficies multicapa es definir varias capas de superficie en el tipo de espesor 'Capas' sin volumen. Pero incluso aquí, los modelos de material se pueden combinar libremente.

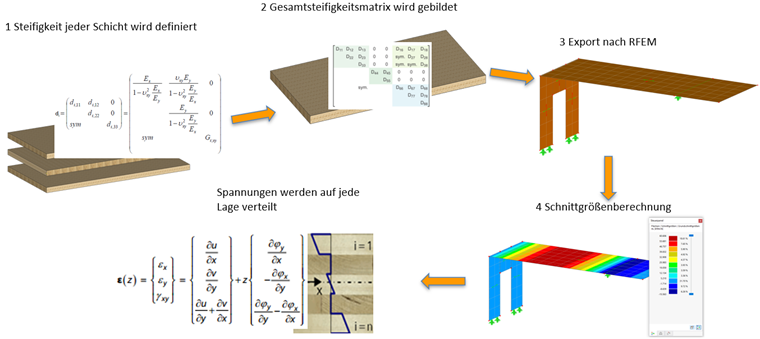
Una vez definidas las capas, el complemento para superficies multicapa genera una matriz de rigidez global de la superficie. En RFEM, para esta superficie se calculan los esfuerzos de corte y las deformaciones. En el complemento de dimensionamiento respectivo, como por ejemplo el dimensionamiento de madera o el cálculo de esfuerzos-deformaciones, estos esfuerzos se distribuyen en las capas existentes. Generalmente, los esfuerzos se muestran en tres puntos de integración por capa.

Flujo de cálculo para superficies multicapa

A continuación, se explica el cálculo de la matriz de rigidez para material isótropo y ortotrópico.

Cálculo de la matriz de rigidez

Como bases de los modelos de material se aplican las siguientes condiciones (ver también el capítulo Materiales del manual de RFEM):

Todos los valores de rigidez deben ser ≥ 0.
La matriz de rigidez global de la superficie debe ser definida positiva.
Ecuación básica isotrópica:

E = 2 G (1 + ν)

E	Módulo de elasticidad
G	Módulo de cortante
ν	deformación transversal

Módulo de elasticidad, módulo de cortante y coeficiente de Poisson

Ecuación básica ortotrópica:

\frac{ν_{y x}}{E_{y}} = \frac{ν_{x y}}{E_{x}}

Relación de la deformación transversal

Matriz de rigidez local de cada capa

Isótropo

d_{i}' = [\begin{matrix} d'_{11, i} & d'_{12, i} & 0 \\ d'_{22, i} & 0 \\ s y m . & d'_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{i}}{1 - ν_{i}^{2}} & \frac{ν_{i} E_{i}}{1 - ν_{i}^{2}} & 0 \\ \frac{E_{i}}{1 - ν_{i}^{2}} & 0 \\ s y m . & G_{i} \end{matrix}] i = 1, . . ., n m i t G_{i} = \frac{E_{i}}{2 (1 + ν_{i})}

Rigidez de la capa de la matriz isótropa

Ortotrópico

d_{i}' = [\begin{matrix} d'_{11, i} & d'_{12, i} & 0 \\ d'_{22, i} & 0 \\ s y m . & d'_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{x, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & \frac{ν_{x y, i} E_{y, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ \frac{E_{y, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ s y m . & G_{x y, i} \end{matrix}] i = 1, . . ., n

Matriz de rigidez ortótropa

Información

Para material ortotrópico, el módulo de corte en el plano de la losa (G_xy) se define a través de los valores del material, mientras que para material isótropo se calcula a partir del módulo E y la contracción lateral. Por lo tanto, para material ortotrópico, la relación de contracción lateral con el principio "lugar-causa" es importante.

Las rigideces de corte para material ortotrópico son las siguientes:

G_xy	Módulo de corte en el plano de la losa (p. ej. 690 N/mm² para C24)
G_xz	Módulo de corte en dirección x a través del espesor (p. ej. 690 N/mm² para C24)
G_yz	Módulo de corte en dirección y a través del espesor (p. ej. 690 N/mm² para C24) - también denominado "módulo de corte por rodadura"

Para material ortotrópico, adicionalmente, se puede definir rigideces dirigidas en una superficie. En el caso estándar, la orientación local en dirección x de la superficie o capa corresponde con la rigidez en dirección x. Sin embargo, dado que se puede definir libremente a través del ángulo β en el tipo de espesor 'Capas', es necesario transformar las rigideces en consecuencia.

d_{i} = [\begin{matrix} d_{11, i} & d_{12, i} & d_{13, i} \\ d_{22, i} & d_{23, i} \\ s y m . & d_{33, i} \end{matrix}] = T_{3 x 3, i}^{T} d'_{i} T_{3 x 3, i}

Rigidez de transformación

T_{3 x 3, i} = [\begin{matrix} c ² & s ² & c s \\ s ² & c ² & - c s \\ - 2 c s & 2 c s & c ² - s ² \end{matrix}] m i t c = \cos (β_{i}), s = \sin (β_{i})

Matriz de transformación

Elemento sumado de cada capa:

d_{11, i} = c^{4} d'_{11, i} + 2 c ² s ² d'_{12, i} + s^{4} d'_{22, i} + 4 c ² s ² d'_{33, i}

d_{12, i} = c^{2} s^{2} d'_{11, i} + s^{4} d'_{12, i} + c^{4} d'_{12, i} + c ² s ² d'_{22, i} - 4 c ² s ² d'_{33, i}

d_{13, i} = c^{3} s d'_{11, i} + c s^{3} d'_{12, i} - c^{3} s d'_{12, i} - c s^{3} d'_{22, i} - 2 c^{3} s d'_{33, i} + 2 c s^{3} d'_{33, i}

d_{22, i} = s^{4} d'_{11, i} + 2 c ² s ² d'_{12, i} + c^{4} d'_{22, i} + 4 c ² s ² d'_{33, i}

d_{23, i} = c s^{3} d'_{11, i} + c^{3} s d'_{12, i} - c s^{3} d'_{12, i} - c^{3} s d'_{22, i} + 2 c^{3} s d'_{33, i} - 2 c s^{3} d'_{33, i}

d_{33, i} = c^{2} s^{2} d'_{11, i} - 2 c ² s ² d'_{12, i} + c^{2} s^{2} d'_{22, i} + {(c^{2} - s^{2})}^{2} d'_{33, i}

Términos individuales por turno

Elementos de flexión y torsión [Nm]

Los elementos de la matriz para flexión y torsión se indican en las siguientes ecuaciones.

D_{11} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{11, i}

Rigidez a la flexión en x

D_{12} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{12, i}

Término de excentricidad (12)

D_{22} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{22, i}

Rigidez a la flexión en y

D_{13} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{13, i}

Término de excentricidad (13)

D_{23} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{23, i}

Término de excentricidad (23)

D_{33} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{33, i}

rigidez a torsión

Con solo una capa en el tipo de espesor 'Capas', el cálculo se lleva a cabo según las ecuaciones explicadas en el manual de RFEM.

Para el corte (elementos D44/55), se aplican ecuaciones diferentes en el tipo de espesor 'Capas'. Se presentan en la sección Corte en el plano de la losa.

Términos de excentricidad [Nm/m]

En las placas asimétricas, se generan términos de excentricidad. Una superficie asimétrica puede surgir, por ejemplo, en un cálculo de protección contra incendios debido a la quema unilateral de una placa de madera contralaminada. Los elementos de la matriz son los siguientes:

D_{16} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{11, i}

Elemento de excentricidad D16

D_{17} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{12, i}

Elemento de excentricidad D17

D_{18} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{13, i}

Elemento de excentricidad D18

D_{27} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{22, i}

Elemento de excentricidad D27

D_{28} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{23, i}

Elemento de excentricidad D28

D_{38} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{33, i}

Elemento de excentricidad D38

Plano del disco [N/m]

En el plano del disco, se tratan las rigideces normales en el plano del disco. Con el elemento D88, se calcula el corte del disco, es decir, la fuerza transversal en el disco. Los elementos de la matriz son los siguientes:

D_{66} = \sum_{i = 1}^{n} t_{i} d_{11, i}

Rigidez axial x D66

D_{67} = \sum_{i = 1}^{n} t_{i} d_{12, i}

Rigidez normal Excéntrica D67

D_{68} = \sum_{i = 1}^{n} t_{i} d_{13, i}

Rigidez normal Excéntrica D68

D_{77} = \sum_{i = 1}^{n} t_{i} d_{22, i}

Rigidez axial y D77

D_{78} = \sum_{i = 1}^{n} t_{i} d_{23, i}

Rigidez normal Excéntrica D78

D_{88} = \sum_{i = 1}^{n} t_{i} d_{33, i}

Placa a cortante D88

Corte en el plano de la losa [N/m]

Para determinar la rigidez al corte, en un material ortotrópico, las rigideces deben rotarse de acuerdo con su orientación respecto al eje local de la superficie. Esto debe hacerse para cada capa del tipo de espesor 'Capas'. Con una estructura sencilla de capas con orientación de 0° de la capa superior y orientación de 90° de la capa inferior, se produce una gran flexibilidad al corte, que debe considerarse correspondientemente en el modelo multicapa. En la imagen siguiente (fuente [1]), se puede observar esto en el ejemplo de una placa de madera contralaminada.

Ilustración de una deformación por cortante en madera contralaminada proporcionada por Informationsdienst Holz

Deformación por corte (Fuente: Informationsdienst Holz)

En la teoría de laminados, la rigidez al corte de una estructura laminada se calcula a través de la transformación de todos los componentes de flexión y corte en las direcciones respectivas de cada capa. Más información se puede encontrar en la literatura indicada a continuación.

Visualización de la orientación de los ejes de rigidez en un laminado para la optimización de las propiedades del material.

Orientación de rigidez

A través de la transformación de la rigidez que se muestra en la imagen, se suman las rigideces. Esta suma también es conocida como "Integral de Grashoff".

D_{44, c a l c}^{"} = \frac{1}{\int_{- t / 2}^{t / 2} \frac{G_{22}^{"} (z)}{G_{11}^{"} (z) G_{22}^{"} (z) - {G_{12}^{"}}^{2} (z)} {(\frac{\int_{z}^{t / 2} E_{x}^{"} (\bar{z}) (\bar{z} - z_{0, x}) d \bar{z}}{\int_{- t / 2}^{t / 2} E_{x}^{"} (\bar{z}) {(\bar{z} - z_{0, x})}^{2} d \bar{z}})}^{2} d z}

Rigidez a cortante en dirección x

Para calcular la rigidez en dirección x e y, se calcula un centro de rigidez para cada estructura de una superficie multicapa.

z_{0, x} = \frac{\int_{- t / 2}^{t / 2} E_{x}^{"} (z) z d z}{\int_{- t / 2}^{t / 2} E_{x}^{"} (z) d z} = \frac{I_{1}}{I_{0}}

Centro de rigidez en x

D_{55, c a l c}^{"} = \frac{1}{\int_{- t / 2}^{t / 2} \frac{G_{11}^{"} (z)}{G_{11}^{"} (z) G_{22}^{"} (z) - {G_{12}^{"}}^{2} (z)} {(\frac{\int_{z}^{t / 2} E_{y}^{"} (\bar{z}) (\bar{z} - z_{0, x}) d \bar{z}}{\int_{- t / 2}^{t / 2} E_{y}^{"} (\bar{z}) {(\bar{z} - z_{0, x})}^{2} d \bar{z}})}^{2} d z}

Rigidez a cortante en dirección y

Centro de rigidez en dirección y:

z_{0, x} = \frac{\int_{- t / 2}^{t / 2} E_{y}^{"} (z) z d z}{\int_{- t / 2}^{t / 2} E_{y}^{"} (z) d z} = \frac{I_{1}}{I_{0}}

Centro de rigidez en dirección y

Para capturar la orientación por capa en el cálculo de la rigidez al corte, las rigideces se registran según las siguientes ecuaciones.

G_{11, i}^{"} = \cos^{2} (φ - ß_{i}) G_{x z, i} + \sin^{2} (φ - ß_{i}) G_{y z, i}

Rigidez a cortante orientada G11

G representa aquí la rigidez al corte de las capas, para evitar confusiones con los elementos de la matriz de rigidez (D).

La rigidez al corte de cada capa también se puede representar en forma de matriz de la siguiente manera:

[\begin{matrix} G_{11} & G_{12} \\ G_{21} & G_{22} \end{matrix}]

Matriz de rigidez a cortante

G_{22, i}^{"} = \sin^{2} (φ - ß_{i}) G_{x z, i} + \cos^{2} (φ - ß_{i}) G_{y z, i}

Rigidez a cortante orientada G22

La rigidez al corte excéntrica en la siguiente ecuación sería siempre nula para la estructura simétrica de madera contralaminada mencionada al principio (0°/90°/0°) y, por lo tanto, no sería relevante. Sin embargo, en una madera contralaminada por ejemplo diagonalmente pegada DLT (Diagonal Laminated Timber), este término de excentricidad no es nulo y, por lo tanto, juega un papel importante.

G_{12}^{"} = (G_{x z, i} - G_{y z, i}) \sin (φ - ß_{i}) \cos (φ - ß_{i})

Rigidez a cortante orientada excéntrica G12

Más información se puede encontrar, entre otros, en [4] y en un video de YouTube.

Cálculo de la rigidez al corte

La rigidez al corte se determina en los siguientes pasos:

Primero se determina el ángulo de máxima rigidez. El ángulo φ indica el cambio del sistema de coordenadas locales x de la superficie a la dirección orientada x''.
Todas las rigideces se rotan en la dirección orientada x'' según las ecuaciones presentadas anteriormente.
La matriz de rigidez del disco de cada capa (3 x 3) se transforma del sistema de coordenadas locales x', y' al sistema rotado x'', y". Además, para calcular la rigidez dirigida al corte de cada capa individual, esto también se lleva a cabo para los módulos de elasticidad de cada capa.

$E_{x, i}^{"} = d_{12, i}^{"} + \frac{2 d_{12, i}^{"} d_{13, i}^{"} d_{23, i}^{"} - d_{22, i}^{"} {(d_{13, i}^{"})}^{2} - d_{33, i}^{"} {(d_{12, i}^{"})}^{2}}{d_{22, i}^{"} d_{33, i}^{"} - {(d_{23, i}^{"})}^{2}}$

Módulo de elasticidad orientado en dirección x

$E_{y, i}^{"} = d_{22, i}^{"} + \frac{2 d_{12, i}^{"} d_{13, i}^{"} d_{23, i}^{"} - d_{11, i}^{"} {(d_{23, i}^{"})}^{2} - d_{33, i}^{"} {(d_{12, i}^{"})}^{2}}{d_{11, i}^{"} d_{33, i}^{"} - {(d_{13, i}^{"})}^{2}}$

Módulo de elasticidad orientado en dirección y
La rigidez al corte se calcula con las ecuaciones descritas anteriormente (Integral de Grashoff). La rigidez al corte se calcula a través de los componentes individuales.

$I = \int_{- h / 2}^{h / 2} d_{11} (z) {(z - z_{0, x})}^{2} d z = \sum_{i = 1}^{n} d_{11, i} \frac{{(z_{m a x, i} - z_{0, x})}^{3} - {(z_{m i n, i} - z_{0, x})}^{3}}{3}$

Segundo momento de inercia en dirección x

$χ_{i} = d_{11, i} \frac{{(z_{m a x, i} - z_{0, x})}^{2}}{2} + \sum_{k = i + 1}^{n} d_{11, k} \frac{{(z_{m a x, i} - z_{0, x})}^{2} - {(z_{m i n, i} - z_{0, x})}^{2}}{2}$

Rigidez equivalente por capa (en x)

Aquí, las ecuaciones se muestran solo para la dirección x (D44). Para la dirección y, se aplica de manera análoga. La rigidez equivalente (componente de Steiner) se calcula para cada capa.
Las rigideces calculadas para la dirección orientada de toda una estructura se recalculan finalmente a través de las relaciones angulares y se muestran en la matriz de rigidez como rigideces originales D44, D55 y D45.

$D_{44} = \cos^{2} (φ) D_{44}^{"} + \sin^{2} (φ) D_{55}^{"}$

Rigidez a cortante recalculada D44

$D_{55} = \sin^{2} (φ) D_{44}^{"} + \cos^{2} (φ) D_{55}^{"}$

Rigidez a cortante recalculada D55

$D_{45} = \sin (φ) \cos (φ) (D_{44}^{"} - D_{55}^{"})$

Rigidez a cortante recalculada D45

Aumento de la rigidez al corte

Puesto que al modelar laminados como superficies también son posibles geometrías con franjas de superficie muy estrechas, en el cálculo de tales geometrías problemáticas, la rigidez al corte debe incrementarse correspondientemente.

En la siguiente ecuación se representa esto para la dirección X

D_{44}^{"} = \max (D_{44, calc}^{"}, \frac{48}{5 l ²} \frac{1}{\frac{1}{\sum_{i = 1}^{n} E_{x, i}^{"} \frac{t_{i}^{3}}{12}} - \frac{1}{\sum_{i = 1}^{n} E_{x, i}^{"} \frac{z_{\max, i}^{3} - z_{\min, i}^{3}}{3}}})

Rigidez a cortante máxima

La longitud l en la ecuación anterior significa aquí la longitud más corta de una caja que se puede colocar sobre la geometría correspondiente.

En otro modelo, que se puede descargar del lado derecho, se comparó una superficie estrecha de un ancho de 10 cm con una superficie idéntica de 20 cm de ancho.

La rigidez al corte de la superficie estrecha es D44=15253kN/m en comparación con D44=5970,8kN/m de la superficie más ancha. Como resultado, a pesar de la carga idéntica, la deformación de la superficie más rígida es menor y la carga de corte es mayor.

Rigideces en superficies multicapa con volúmenes integrados

En el futuro, en el complemento de superficies multicapa también será posible definir volúmenes junto con superficies. En este tipo, una superficie también se exportará a RFEM. Como la generación de rigideces y la descomposición de esfuerzos requieren más esfuerzo, esto se explicará por separado.

Referencias

Construcción con madera contralaminada, elementos de madera maciza portantes para paredes, techos y tejados.
Estructuras superficiales planas: fundamentos del modelado y cálculo de muros y losas
Jones, R. M. (s.f.). Mechanics of Composite Materials (2ª ed.). Taylor & Francis Inc., Filadelfia.
Arnold, M.: "Propiedades mecánicas de la madera laminada diagonalmente (DLT) con respecto a las losas de madera maciza apoyadas en punto". Tesis doctoral en elaboración. Cátedra de Estructuras de madera y construcción de edificios, Universidad Técnica de Múnich, 2023.

Capítulo principal

Teoría

Modelo

585x

23x

Modelos multicapa

Modelo multicapa en rigidizador a cortante

70x

rigidez a cortante