Online manuály RFEM 6 | Vícevrstvé plochy

Zpět k online manuálům

2263x

003626

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

19.10.2023

Vybrat manuál

Přehled

Addon Vícevrstvé plochy

Teorie

Vstupní údaje

Výsledky

Příklady výpočtů

Tuhosti pro vícevrstvé plochy

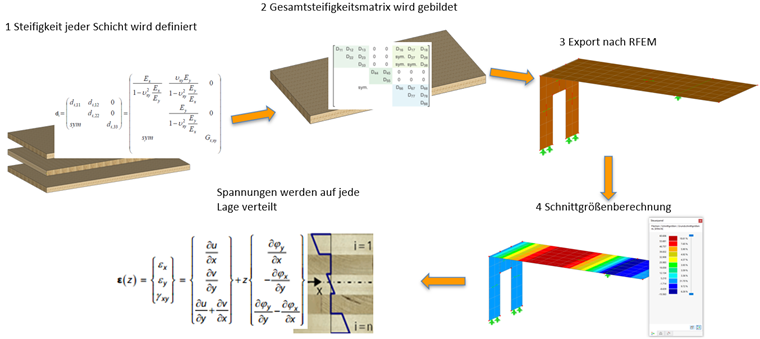
Materiálové modely

Základem pro složení vícevrstvých ploch do efektivní tuhosti plochy jsou materiálové modely. S modulem Vícevrstvé plochy lze materiálové modely volně kombinovat v programu RFEM 6. Základy materiálových modelů jsou popsány v kapitolách Materiály a Nelineární chování materiálu příručky RFEM.

Výběr kombinací materiálových modelů je k dispozici v modelu "Vícevrstvé modely" (viz pravý sloupec), který si můžete stáhnout pro další studium kombinací.

Následující seznam ukazuje výběr možných kombinací:

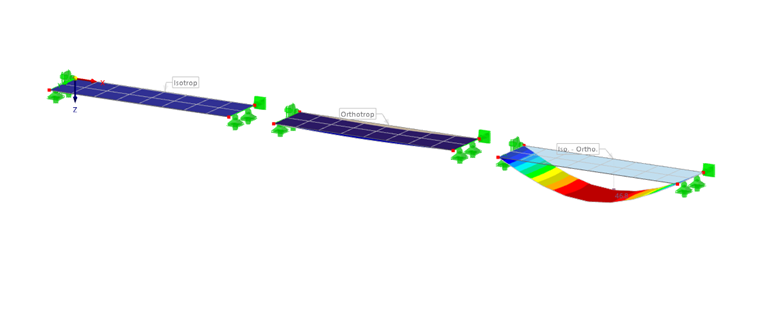
Izotropní vrstvy (např. beton - ocel)
Ortotropní vrstvy (např. křížem lepené dřevo)
Izotrop - ortotrop (např. ocel - GFK)
Izotrop plastický - izotrop (např. beton - ocel)
Izotrop nelineárně pružný - ortotrop (např. beton - dřevo)
Izotrop - ortotrop plastický (např. beton - dřevo)
Izotrop poškození - ortotrop (např. beton - dřevo)

Informace

Pro kombinaci nelineárních materiálů musí být aktivován modul Nelineární chování materiálu.

Tuhosti u vícevrstvých ploch bez objemu

Jednodušší variantou výpočtu v modulu Vícevrstvé plochy je definovat různé vrstvy ploch v tloušťkovém typu 'Vrstev' bez objemu. Také zde lze volně kombinovat materiálové modely.

Když jsou vrstvy definovány, modul Vícevrstvé plochy vytvoří globální matici tuhosti plochy. V RFEM se pro tuto plochu počítají vnitřní síly a deformace. V příslušném modulu pro posouzení, jako je například Posouzení dřeva nebo Výpočet napětí-deformace, jsou tyto vnitřní síly pak rozděleny do jednotlivých vrstev. Obvykle jsou vnitřní síly vydávány ve třech integračních bodech na vrstvě.

Postup výpočtu pro vícevrstvé plochy

Následuje vysvětlení výpočtu matice tuhosti pro izotropní a ortotropní materiál.

Výpočet matice tuhosti

Základy materiálových modelů zahrnují následující podmínky (viz také kapitola Materiály příručky RFEM):

Všechny hodnoty tuhosti ≥ 0
Celková matice tuhosti plochy musí být pozitivně definitní.
Základní rovnice izotropní:

E = 2 G (1 + ν)

E	Modul pružnosti
G	Smykový modul
ν	Poissonův součinitel

Modul pružnosti, Smykový modul a Poissonův poměr

Základní rovnice ortotropní:

\frac{ν_{y x}}{E_{y}} = \frac{ν_{x y}}{E_{x}}

Vztah příčného přetvoření

Lokální matice tuhosti každé vrstvy

Izotropní

d_{i}' = [\begin{matrix} d'_{11, i} & d'_{12, i} & 0 \\ d'_{22, i} & 0 \\ s y m . & d'_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{i}}{1 - ν_{i}^{2}} & \frac{ν_{i} E_{i}}{1 - ν_{i}^{2}} & 0 \\ \frac{E_{i}}{1 - ν_{i}^{2}} & 0 \\ s y m . & G_{i} \end{matrix}] i = 1, . . ., n m i t G_{i} = \frac{E_{i}}{2 (1 + ν_{i})}

Vrstva matice tuhosti izotropní

Ortotropní

d_{i}' = [\begin{matrix} d'_{11, i} & d'_{12, i} & 0 \\ d'_{22, i} & 0 \\ s y m . & d'_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{x, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & \frac{ν_{x y, i} E_{y, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ \frac{E_{y, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ s y m . & G_{x y, i} \end{matrix}] i = 1, . . ., n

Vrstva matrice tuhosti ortotropní

Informace

U ortotropního materiálu je smykový modul v rovině desky (G_xy) definován na základě materiálových hodnot, zatímco u izotropního materiálu je odvozen z modulu pružnosti a míry příčného zkrácení. Proto u ortotropního materiálu je zásadní vztah "příčina-účinek" příčných deformací.

Smykové tuhosti pro ortotropní materiál jsou následující:

G_xy	Smykový modul v rovině desky (např. 690 N/mm² pro C24)
G_xz	Smykový modul v směru x přes tloušťku (např. 690 N/mm² pro C24)
G_yz	Smykový modul v směru y přes tloušťku (např. 690 N/mm² pro C24) – také nazýván "smykový modul valivého smyku"

U ortotropního materiálu je dále výjimečné, že lze definovat směrové tuhosti v ploše. Ve standardním případě odpovídá lokální orientace plochy nebo vrstvy ve směru x tuhosti ve směru x. Protože to však může být volně definováno úhlem β v tloušťkovém typu 'Vrstev', je nutné tuhosti odpovídajícím způsobem transformovat.

d_{i} = [\begin{matrix} d_{11, i} & d_{12, i} & d_{13, i} \\ d_{22, i} & d_{23, i} \\ s y m . & d_{33, i} \end{matrix}] = T_{3 x 3, i}^{T} d'_{i} T_{3 x 3, i}

Transformační tuhosti

T_{3 x 3, i} = [\begin{matrix} c ² & s ² & c s \\ s ² & c ² & - c s \\ - 2 c s & 2 c s & c ² - s ² \end{matrix}] m i t c = \cos (β_{i}), s = \sin (β_{i})

Transformační matice

Složený element každé vrstvy:

d_{11, i} = c^{4} d'_{11, i} + 2 c ² s ² d'_{12, i} + s^{4} d'_{22, i} + 4 c ² s ² d'_{33, i}

d_{12, i} = c^{2} s^{2} d'_{11, i} + s^{4} d'_{12, i} + c^{4} d'_{12, i} + c ² s ² d'_{22, i} - 4 c ² s ² d'_{33, i}

d_{13, i} = c^{3} s d'_{11, i} + c s^{3} d'_{12, i} - c^{3} s d'_{12, i} - c s^{3} d'_{22, i} - 2 c^{3} s d'_{33, i} + 2 c s^{3} d'_{33, i}

d_{22, i} = s^{4} d'_{11, i} + 2 c ² s ² d'_{12, i} + c^{4} d'_{22, i} + 4 c ² s ² d'_{33, i}

d_{23, i} = c s^{3} d'_{11, i} + c^{3} s d'_{12, i} - c s^{3} d'_{12, i} - c^{3} s d'_{22, i} + 2 c^{3} s d'_{33, i} - 2 c s^{3} d'_{33, i}

d_{33, i} = c^{2} s^{2} d'_{11, i} - 2 c ² s ² d'_{12, i} + c^{2} s^{2} d'_{22, i} + {(c^{2} - s^{2})}^{2} d'_{33, i}

Jednotlivé termíny za směnu

Ohybové a torzní elementy [Nm]

Elementy matice pro ohyb a torzi jsou uvedeny v následujících rovnicích.

D_{11} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{11, i}

Ohybová tuhost v x

D_{12} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{12, i}

Člen excentricity (12)

D_{22} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{22, i}

Ohybová tuhost v y

D_{13} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{13, i}

Člen excentricity (13)

D_{23} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{23, i}

Člen excentricity (23)

D_{33} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{33, i}

Torzní tuhost

Při jedné vrstvě v tloušťkovém typu 'Vrstev' se výpočet provádí podle rovnic objasněných v příručce RFEM.

Pro smyk (elementy D44/55) se v tloušťkovém typu 'Vrstev' používají jiné rovnice. Budou představeny v oddílu Smyk v rovině desky.

Excentricitní členy [Nm/m]

U nesymetrických desek se vyskytují excentricitní členy. Asymetrická plocha může například vzniknout u posouzení požární odolnosti jednostranným uhořením křížem lepené desky. Elementy matice jsou následující:

D_{16} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{11, i}

Prvek excentricity D16

D_{17} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{12, i}

Prvek excentricity D17

D_{18} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{13, i}

Prvek excentricity D18

D_{27} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{22, i}

Prvek excentricity D27

D_{28} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{23, i}

Prvek excentricity D28

D_{38} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{33, i}

Prvek excentricity D38

Rovinný režim [N/m]

V rovině desky se řeší normálové tuhosti v rovině desky. S elementem D88 se vypočítá smyk v rovině desky – tedy příčná síla v desce. Elementy matice jsou následující:

D_{66} = \sum_{i = 1}^{n} t_{i} d_{11, i}

Osová tuhost x D66

D_{67} = \sum_{i = 1}^{n} t_{i} d_{12, i}

Normálová tuhost Excentrická D67

D_{68} = \sum_{i = 1}^{n} t_{i} d_{13, i}

Normálová tuhost Excentrická D68

D_{77} = \sum_{i = 1}^{n} t_{i} d_{22, i}

Osová tuhost y D77

D_{78} = \sum_{i = 1}^{n} t_{i} d_{23, i}

Normálová tuhost Excentrická D78

D_{88} = \sum_{i = 1}^{n} t_{i} d_{33, i}

Smyk desek D88

Smyk v rovině desky [N/m]

Pro stanovení smykové tuhosti je u ortotropního materiálu nutné tuhosti transformovat podle jejich orientace vůči lokální ose plochy. To se musí provést pro každou vrstvu tloušťkového typu 'Vrstev'. U jednoduchého vrstevnatého složení s 0° orientací krycí vrstvy a 90° orientací podkladové vrstvy se dosahuje velké smykové poddajnosti, kterou je nutné zohlednit u vícevrstvého modelu. V následujícím obrázku (zdroj [1]) je to patrné na příkladu křížem lepené desky.

Znázornění smykové deformace v křížem lepeném dřevě, poskytnuté informační službou pro dřevo.

Smykové zkreslení (Zdroj: Informationsdienst Holz)

V teorii laminátu je smyková tuhost vrstvené konstrukce vypočítána transformací všech ohybových a smykových složek do příslušných směrů každé vrstvy. Další informace k tomuto tématu naleznete mimo jiné v níže uvedené literatuře.

Vizualizace uspořádání os tuhosti ve vrstveném materiálu za účelem optimalizace materiálových vlastností

Orientace tuhosti

Prostřednictvím na obrázku znázorněné transformace tuhostí jsou tuhosti sumovány. Tato sumační metoda je také známá jako "Grashoffův integrál".

D_{44, c a l c}^{"} = \frac{1}{\int_{- t / 2}^{t / 2} \frac{G_{22}^{"} (z)}{G_{11}^{"} (z) G_{22}^{"} (z) - {G_{12}^{"}}^{2} (z)} {(\frac{\int_{z}^{t / 2} E_{x}^{"} (\bar{z}) (\bar{z} - z_{0, x}) d \bar{z}}{\int_{- t / 2}^{t / 2} E_{x}^{"} (\bar{z}) {(\bar{z} - z_{0, x})}^{2} d \bar{z}})}^{2} d z}

Smyková tuhost ve směru x

Pro výpočet tuhosti ve směru x a y se pro každou konstrukci vícevrstvého povrchu vypočítá tzv. těžiště tuhosti.

z_{0, x} = \frac{\int_{- t / 2}^{t / 2} E_{x}^{"} (z) z d z}{\int_{- t / 2}^{t / 2} E_{x}^{"} (z) d z} = \frac{I_{1}}{I_{0}}

Střed tuhosti v x

D_{55, c a l c}^{"} = \frac{1}{\int_{- t / 2}^{t / 2} \frac{G_{11}^{"} (z)}{G_{11}^{"} (z) G_{22}^{"} (z) - {G_{12}^{"}}^{2} (z)} {(\frac{\int_{z}^{t / 2} E_{y}^{"} (\bar{z}) (\bar{z} - z_{0, x}) d \bar{z}}{\int_{- t / 2}^{t / 2} E_{y}^{"} (\bar{z}) {(\bar{z} - z_{0, x})}^{2} d \bar{z}})}^{2} d z}

Smyková tuhost ve směru y

Těžiště tuhosti ve směru y:

z_{0, x} = \frac{\int_{- t / 2}^{t / 2} E_{y}^{"} (z) z d z}{\int_{- t / 2}^{t / 2} E_{y}^{"} (z) d z} = \frac{I_{1}}{I_{0}}

Střed tuhosti ve směru y

Aby se ve výpočtu smykové tuhosti zachytila orientace každé vrstvy, jsou tuhosti zaznamenány podle následujících rovnic.

G_{11, i}^{"} = \cos^{2} (φ - ß_{i}) G_{x z, i} + \sin^{2} (φ - ß_{i}) G_{y z, i}

Orientovaná smyková tuhost G11

G zde znamená smykovou tuhost vrstev, aby nedošlo k záměně s elementy matice tuhosti (D).

Také smyková tuhost každé vrstvy může být vyjádřena v maticovém tvaru následovně:

[\begin{matrix} G_{11} & G_{12} \\ G_{21} & G_{22} \end{matrix}]

Matice smykové tuhosti

G_{22, i}^{"} = \sin^{2} (φ - ß_{i}) G_{x z, i} + \cos^{2} (φ - ß_{i}) G_{y z, i}

Orientovaná smyková tuhost G22

Excentrická smyková tuhost v následující rovnici by u výše zmíněné symetrické konstrukce křížem lepeného dřeva (0°/90°/0°) vždy byla nulová a nebyla by tedy relevantní. U např. diagonálně lepeného dřeva DLT (Diagonal Laminated Timber) však tento excentricitní člen není nulový a hraje důležitou roli.

G_{12}^{"} = (G_{x z, i} - G_{y z, i}) \sin (φ - ß_{i}) \cos (φ - ß_{i})

Excentricky orientovaná smyková tuhost G12

Další informace naleznete mimo jiné v [4] a na YouTube videu.

Výpočet smykové tuhosti

Smyková tuhost se získává následujícími kroky:

Nejprve je určeno úhel maximální tuhosti. Úhel φ ukazuje změnu lokálního souřadnicového systému x plochy na orientovaný směr x''.
Všechny tuhosti se transformují do orientovaného směru x'' podle výše uvedených rovnic.
Plátnová tuhostní matice každé vrstvy (3 x 3) je transformována z lokálního souřadnicového systému x', y' do otočeného systému x'', y". Kromě výpočtu směrové smykové tuhosti každé jednotlivé vrstvy se toto provádí i pro moduly pružnosti každé vrstvy.

$E_{x, i}^{"} = d_{12, i}^{"} + \frac{2 d_{12, i}^{"} d_{13, i}^{"} d_{23, i}^{"} - d_{22, i}^{"} {(d_{13, i}^{"})}^{2} - d_{33, i}^{"} {(d_{12, i}^{"})}^{2}}{d_{22, i}^{"} d_{33, i}^{"} - {(d_{23, i}^{"})}^{2}}$

Orientovaný modul pružnosti ve směru x

$E_{y, i}^{"} = d_{22, i}^{"} + \frac{2 d_{12, i}^{"} d_{13, i}^{"} d_{23, i}^{"} - d_{11, i}^{"} {(d_{23, i}^{"})}^{2} - d_{33, i}^{"} {(d_{12, i}^{"})}^{2}}{d_{11, i}^{"} d_{33, i}^{"} - {(d_{13, i}^{"})}^{2}}$

Orientovaný modul pružnosti ve směru y
Smyková tuhost se počítá pomocí výše popsaných rovnic (Grashoffův integrál). Smyková tuhost se vypočítá přes jednotlivé složky.

$I = \int_{- h / 2}^{h / 2} d_{11} (z) {(z - z_{0, x})}^{2} d z = \sum_{i = 1}^{n} d_{11, i} \frac{{(z_{m a x, i} - z_{0, x})}^{3} - {(z_{m i n, i} - z_{0, x})}^{3}}{3}$

Moment setrvačnosti plochy ve směru x

$χ_{i} = d_{11, i} \frac{{(z_{m a x, i} - z_{0, x})}^{2}}{2} + \sum_{k = i + 1}^{n} d_{11, k} \frac{{(z_{m a x, i} - z_{0, x})}^{2} - {(z_{m i n, i} - z_{0, x})}^{2}}{2}$

Ekvivalentní tuhost na vrstvu (v x)

Zde jsou rovnice ukázány pouze pro směr x (D44). Toto platí analogicky i pro směr y. Ekvivalentní tuhost (Steinerův podíl) se vypočítá pro každou vrstvu.
Vypočítané tuhosti pro orientovaný směr celkové konstrukce se nakonec zpětně převedou přes úhlové vztahy a jsou uvedeny jako původní tuhosti D44, D55 a D45 v matici tuhosti.

$D_{44} = \cos^{2} (φ) D_{44}^{"} + \sin^{2} (φ) D_{55}^{"}$

Přepočítaná smyková tuhost D44

$D_{55} = \sin^{2} (φ) D_{44}^{"} + \cos^{2} (φ) D_{55}^{"}$

Přepočítaná smyková tuhost D55

$D_{45} = \sin (φ) \cos (φ) (D_{44}^{"} - D_{55}^{"})$

Přepočítaná smyková tuhost D45

Zvýšení smykové tuhosti

Jelikož při modelování laminátů jako plochy je také možné pracovat s geometriemi s velmi úzkými plochými pásy, musí se při výpočtu takových problematických geometrických útvarů smyková tuhost odpovídajícím způsobem zvětšit.

V následující rovnici je to znázorněno pro směr X

D_{44}^{"} = \max (D_{44, calc}^{"}, \frac{48}{5 l ²} \frac{1}{\frac{1}{\sum_{i = 1}^{n} E_{x, i}^{"} \frac{t_{i}^{3}}{12}} - \frac{1}{\sum_{i = 1}^{n} E_{x, i}^{"} \frac{z_{\max, i}^{3} - z_{\min, i}^{3}}{3}}})

Maximální smyková tuhost

Délka l v výše uvedené rovnici znamená v tomto případě nejkratší délku krabice, která může být přes příslušnou geometrii položena.

V dalším modelu, který je možno si stáhnout na pravé straně, byla porovnána úzká plocha o šířce 10 cm s identickou plochou o šířce 20 cm.

Smyková tuhost úzké plochy činí D44=15253kN/m oproti D44=5970,8kN/m širší plochy. Výsledkem toho je, že i přes identické zatížení je deformace tužší plochy menší a smykové zatížení větší.

Tuhosti u vícevrstvých ploch s integrovaným objemem

V budoucnu bude v modulu Vícevrstvé plochy také možné definovat objem společně s plochami. U tohoto typu bude také plocha exportována do RFEM. Jelikož generování tuhostí a rozklad vnitřních sil je náročnější, bude to podrobněji objasněno.

Reference

Stavby z křížem lepeného dřeva
Nosné prvky z masivního dřeva pro stěny, stropy a střechy – řada 4, díl 6, svazek 1
Informační služba Holz, Berlín, 2016
Ploché povrchové nosné konstrukce: Základy modelování a výpočtu stěn a desek
Jones, R. M. (n.d.). Mechanics of Composite Materials (2nd ed.). Taylor & Francis Inc., Philadelphia.
Arnold, M. (2024). Mechanical Properties of Diagonal Laminated Timber (DLT) with Respect to Point-Supported Mass Timber Slabs (dizertace). Munich, Technical University of Munich – Předseda pro dřevěné konstrukce a stavbu budov.

Nadřazená kapitola

Teorie

Model

585x

23x

Vícevrstvé modely

70x

Smyková tuhost