Основы диаграмм соединения
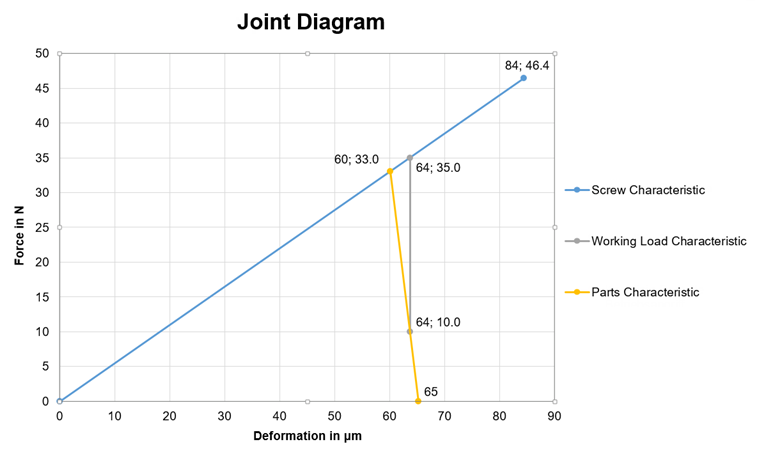
Диаграмма соединения - это графическое представление сил в предварительно напряженном болтовом соединении. В данном случае сжимающие силы, возникающие в соединяемых элементах, и соответствующие деформации противопоставляются силам и деформациям в болте. Такая диаграмма показана на Рисунке 01.
Синяя линия (характерная линия) представляет собой график болта, а желтая - график конструктивных элементов. Как правило, жесткость болта меньше, чем жесткость элементов конструкции. Однако существуют также различные исключения, например, в случае с гайками. Пересечение обеих линий представляет собой силу предварительного нагружения в соединении без приложенной внешней нагрузки. Конечная точка линии болта - это максимальная сила сопротивления в резьбе.
Кроме линии болтов и линии компонента, существует еще одна важная характерная линия внешней растягивающей силы (также предварительного нагружения). Эта линия показана серым цветом на рисунке 01. Она исходит из характеристической линии компонентов на оси y требуемой остаточной силы смыкания. Остаточная сила смыкания - это сила, которая все еще удержит компоненты вместе. Например, если в соединении есть горизонтальная сила, которую необходимо поглотить (без поперечной деформации болта, т.е. только за счет составляющей трения) в дополнение к растягивающей составляющей при существующей рабочей нагрузке, то остаточная сила зажатия должны быть выбраны таким образом, чтобы обеспечить достаточную прочность.
Кроме данных характерных линий, существуют другие линии, которые можно использовать для более подробного представления. Поскольку данные линии не влияют на основной процесс расчета, мы не будем их объяснять в данной статье, а будем использовать лишь представленную упрощенную диаграмму соединения. Например, дополнительные характерные линии могут быть вызваны деформацией при сжатии или внецентренным напряжением и нагрузкой.
Формулы упрощенной диаграммы соединения
Чтобы создать диаграмму соединения, необходимо сначала рассчитать соответствующие жёсткости, деформации и силы. В общем случае, жесткость пружины можно рассчитать по закону Гука следующим образом:
где
c - жесткость (постоянная пружины),
F = сила пружины
f - деформация (прогиб).
В случае растянутого стержня из изотропного материала, постоянную пружины можно рассчитать напрямую через модуль упругости (модуль упругости):
где
E - модуль упругости,
A - площадь сечения растянутого стержня,
l - длина растянутого стержня.
Жесткость болта упрощается, и применяется только стержень болта. Другие варианты выбора - применить головку болта, резьбу, гайку, различные диаметры стержней и т.д. В таком случае, элементы с их обратными значениями добавляются к общей жесткости. Жесткость пружины болта рассчитывается по следующей формуле (инструмент S):
где
cS - жесткость пружины болта,
ES - модуль упругости болта,
AS - площадь сечения болта,
lK - длина зажима (высота/толщина элементов).
Диаметр боковой поверхности резьбы d3 применяется для площади сечения в области резьбы болта. Таким образом, получается общая формула:
Аналогичным образом рассчитывается и жесткость компонента. Поскольку имеется одна или несколько плит, используется индекс P:
где
cP - жесткость пружины компонентов/плит,
EP - модуль упругости плит,
AP - площадь сечения пластин,
lK - длина зажима (высота/толщина элементов).
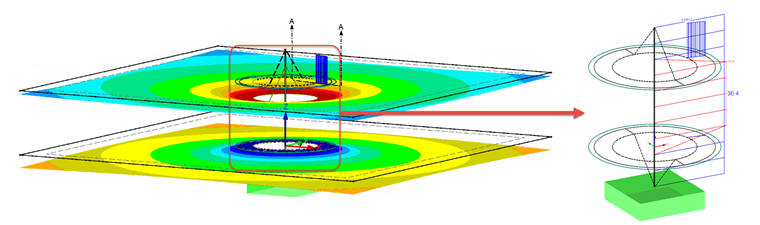
Площадь сечения AP в отличие от болта зависит от толщины. Предполагается, что нагрузка распространяется под углом около 60°. Существуют три различных случая, как показано на рисунке 02.
В случае 1 компоненты между болтом и гайкой представляют собой гильзу, диаметр которой максимально равен диаметру опорной поверхности болта или гайки.
Случай 2 охватывает диапазон, в котором диаметр гильзы минимально равен диаметру опорной поверхности гайки или болта, а максимально равен диаметру конуса расширения нагрузки (отмечено красным цветом на рисунке 02). Он растягивается симметрично с обеих сторон, а диаметр является наибольшим в середине длины зажима.
Случай 3 охватывает диапазон от максимального конуса удлинения нагрузки до бесконечного удлинения плиты. Поэтому необходимо рассчитать замещающую площадь Aers. Aers соответствует площади сечения сменного цилиндра с постоянным расширением нагрузки.
В нашем примере достаточно случая 3. Aers рассчитывается по следующей формуле (см. VDI 2230, издание 1986 [1] ):
где
dW - диаметр опорной поверхности,
dh - диаметр отверстия.
Диаметр опорной поверхности может быть упрощенно применен в качестве 90% ширины поперек граней:
dW = 0,9 ∙ s (3.3)
где
s - ширина по граням головки болта/гайки.
Поскольку в плоскостной модели точка приложения нагрузки не обязательно находится наверху элемента (плиты), а всегда находится в середине поверхности, жесткость плиты необходимо определять в этой точке приложения нагрузки. Для этого вводится коэффициент приложения нагрузки n, который соответственно уменьшает длину зажима. Данная проблема показана на рисунке 03.
Фактические компоненты (в данном случае две плиты) будут уменьшены до середины поверхности. В случае двух пластин n всегда равно 0,5, так как всегда используется половина каждой пластины. Новая жесткость плиты cPn затем рассчитывается следующим образом:
где
ΦK - коэффициент нагрузки.
Для создания характерных линий затем требуются, кроме жесткостей, также различные силы. Далее необходимо указать остаточную нагрузку на зажим FKR, рабочую нагрузку FA и коэффициент затяжки αA (затяжка с контролируемым углом). Результирующие минимальные и максимальные монтажные силы FMmin и FMmax, наоборот, должны быть рассчитаны. Формула для определения предварительных нагружений при затяжке с контролируемым углом:
FMmin = FKmin + FPA (3.6)
FMmax = αA ∙ FMmin (3.7)
где
αA - коэффициент ужесточения для метода с контролем угла,
FKmin - минимальная требуемая остаточная сила смыкания в соединении,
FPA - это дополнительная нагрузка на плиту от рабочей нагрузки.
Дополнительная нагрузка на плиту FPA - это сила, возникающая при приложении рабочей нагрузки. Рассчитывается по формуле:
FPA = (1 - n ∙ ΦK ) ∙ FA (3.8)
где
FA - рабочая нагрузка.
При упрощении без учета осадки сила предварительного напряжения FV соответствует минимальной силе предварительного напряжения FMmin. Для учета кривой рабочей нагрузки не хватает максимальной силы в болте FSmax, которая возникает в болте при отношении рабочей нагрузки:
FSmax = FMmax + FSA (3.9)
где
FSA - дополнительная сила в болтах.
Дополнительная сила в болтах FSA снова рассчитывается аналогично формуле 3.8:
FSA = n∙ ΦK ∙ FA (3.10)
Максимальная несущая способность болта (F0,2 ) как последняя недостающая сила должна определяться с помощью площади сечения болта в резьбе. Она рассчитывается с помощью диаметра площади сечения ds, который является результатом среднего значения диаметра ядра dk (d3 ) и диаметра боковой поверхности dfl (d2 ):
где
d2 - диаметр резьбы по боковой поверхности,
d3 - диаметр ядра резьбы,
fub - прочность материала болта на растяжение.
В дополнение к силам, деформации должны быть заданы в виде соответствующих значений, чтобы характерные линии можно было ввести в диаграмму соединения. Для этого применяется формула 1.1, преобразованная по f. Ниже приведены формулы для преобразования деформаций f в соответствующие силы F:
В результате мы получим следующие точки/значения линии для диаграммы соединения:
| Характерная линия | Деформация | Сила |
|---|---|---|
| Болт | 0 | 0 |
| f0,2 | f0,2 | |
| Пластина | fSMmax | FMmax |
| fSMmax + fPMmax или fMmax | 0 | |
| Рабочая нагрузка | fSMmax + fSA | FMmax - FPA |
| fSMmax + fSA | FMmax + FSA = FSmax |
Таблица 1 - Точки на линии/значения для диаграммы соединения
Моделирование преднапряженных болтовых соединений в программе RFEM
Модель должна представлять собой хорошее сочетание точности и практичности. Таким образом, соединение будет состоять из поверхностей, стержней и контактных тел.
Для примера расчета мы зададим следующие параметры:
FA = 25 кН
FK = 10 кН
ES = EP = 210 000 Н/мм²
t1 = t2 = 10 мм
lK = t1 + t2 = 20 мм
dh = 10 мм
DA > dW + lK
n = 0,5
αA = 1,0
Болт:
M10 8,8
fub = 800 Н/мм²
d2 = 9,03 мм
d3 = 8,16 мм
s = 17 мм
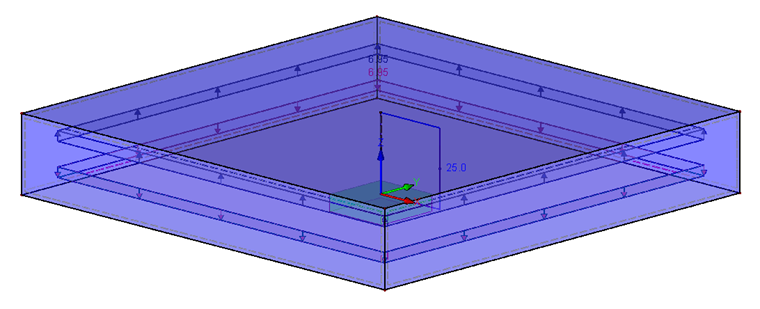
Модель состоит из двух наложенных друг на друга квадратных поверхностей с отверстием (диаметр dh ) в середине, которые имеют размеры 60 x 60 мм (для выполнения DA > dW + lK ). Поскольку t1 = t2, шаг пластин равен 10 мм. Нагрузка действует прямо в середине плиты (нейтральное волокно). Таким образом, результирующее n равно 0,5. Модель опирается на неподвижную опору на нижнем конце стержня. Для достижения общей опорной реакции, равной нулю, нагрузка должна быть приложена как к верхней, так и к нижней плите. Нагрузка составляет 6,95 Н/мм² для 25 кН общей силы.
Для хорошей передачи нагрузки между болтом (балкой) и пластинами, вокруг отверстия моделируется жесткая поверхность (кольцо) с наружным диаметром dW. Соединение между плитами создадим с помощью трех контактных тел. Одно тело находится вокруг отверстия без жесткой части поверхности; два контактных тела опираются вокруг отверстия, как две оболочки. Контактные тела должны иметь тот же материал, что и пластины, для точного отражения жесткости между пластинами. Кроме того, контакт выходит из работы при подъеме и имеет жесткое трение в горизонтальном направлении с коэффициентом 0,1.
Конструкция показана на рисунке 04. Номером 1 показаны поверхности и стержни с фактическими размерами. Под номером 2 показана верхняя поверхность с балкой (болтом) и жесткими стержнями, которые представляют собой соединение между болтом и плитой. Жесткая поверхность (розовые) также имеет жесткий стержень на внутреннем крае для передачи любых моментов.
Другим важным моментом является сетка КЭ. Из-за малых размеров, основной размер сетки КЭ для lКЭ был задан равным 2 мм. Кроме того, на жестких поверхностях было задано уплотнение сетки поверхности с lКЭ 0,2 мм.
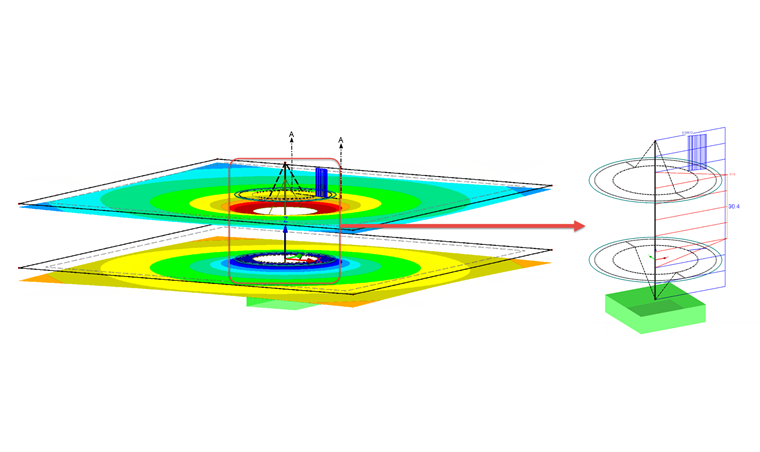
Поскольку на практике ни диаметр болта, ни рабочая сила на болте не известны, можно смоделировать конструкцию без отверстия и применить жесткий стержень вместо балки для первого расчета модели и для определения силы в болтах. Эта модель для предварительного определения размеров показана на рисунке 05.
Чтобы можно было определить остаточное предварительное напряжение в модели, параллельно болту был прикреплен результирующий стержень (расстояние 0,1 мм). Сюда входят все внутренние силы контактного тела.
Сравнение аналитического и численного решения
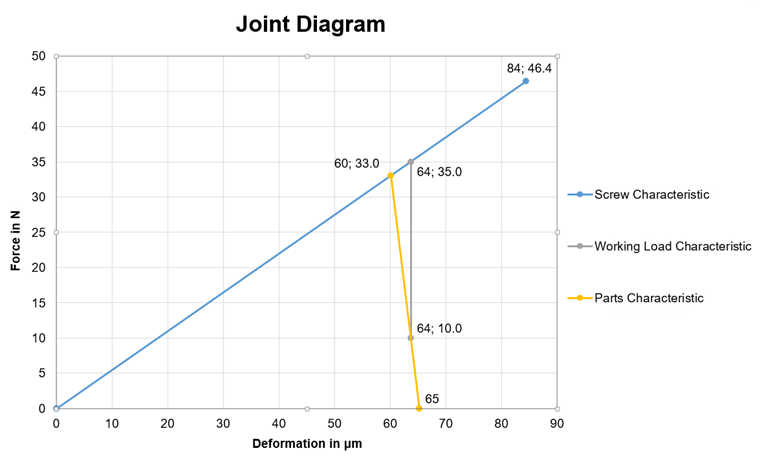
Для сравнения решений необходимо сначала создать диаграмму соединений. Требуемые значения указаны в таблице 1. Промежуточные значения и характеристические линии, показанные в таблице 2, получены путем замены значений из практического примера (см.выше). Таблица 3 включает в себя сводку наиболее важных значений, аналогичной таблице 1, а на рисунке 06 показана полная диаграмма соединения.
| Символ | Номер формулы | Значение |
|---|---|---|
| C[SCHOOL.NOTES] | 2.2 | 549 кН/мм |
| Aers | 3.2 | 303 мм² |
| CP | 3.1 | 3 182 кН/мм |
| ΦK | 3,5 | 0,147 |
| CPn | 3.4 | 6 921 кН/мм |
| fSA | 3.10 | 1,8 кН |
| fSA | 4.4 | 3 мм |
| FPA | 3.8 | 23,2 кН |
| FMmax | 3.6, 3.7 | 33,2 кН |
| fSMmax | 4.2 | 60 мм |
| fMmax | 4.3 | 65 мм |
| f0,2 | 3,11 | 46,2 кН |
| f0,2 | 4.1 | 84 мм |
Таблица 2 - Промежуточные результаты и результаты расчетного примера
| Характерная линия | Деформация [μm] | Сила [кН] |
|---|---|---|
| Болт | 0 | 0,0 |
| 84 | 46,2 | |
| Пластина | 60 | 33,2 |
| 65 | 33,2 | |
| Рабочая нагрузка | 63 | 10,0 |
| 63 | 35,0 |
Таблица 3 - Характерные точки линии/значения для примера расчета
Сначала для численного решения были созданы два загружения. Первое загружение (ЗГ1 Предварительное напряжение) включает в себя нагрузку предварительного напряжения на стержень, а второй случай (ЗГ2 Рабочая нагрузка) - рабочую нагрузку. Кроме того, было создано сочетание нагрузок обоих загружений (коэффициент 1,0) (СН1: ЗГ1 + ЗГ2). Расчет основан на линейном статическом анализе с 15 приращениями нагрузки (лучшая сходимость в случае контактных тел с выходом из работы).
Что касается предварительного напряжения, то в данном случае можно применить тип нагрузки на стержень - начальное предварительное напряжение или конечное предварительное напряжение. Фактическая предварительная нагрузка и есть конечное предварительное напряжение. Поскольку конечная нагрузка предварительного напряжения требует большого времени для вычисления, рекомендуется использовать нагрузку начального предварительного напряжения на стержень. Однако тот имеет недостаток, что данная нагрузка не включает в себя противодействующую силу через плиты. Таким образом, после расчета осевая сила в стержне слишком мала, поскольку часть стержня может быть уменьшена за счет деформации пластин. Эта разница может быть уменьшена двумя способами. Во-первых, ее можно спрогнозировать на основе деформации плиты и преобразовать в дополнительную силу FZus,v (прогнозируемую) по следующей формуле:
FZus,v = fPMmax ∙ cS (5.1)
В то же время, его можно определить итеративно. Для этого необходимо рассчитать нагружение в преднапряжении. Разница между приложенным начальным предварительным напряжением и результирующей нормальной силой в стержне соответствует дополнительной силе FZus,i (итерационная). Можно применить следующую формулу:
FZus,i = FMmax - NS (5.2)
где
NS - нормальная сила в стержне при начальном предварительном напряжении FMmax.
Дополнительная сила FZus,v определяется по значениям в таблице 2 следующим образом:
FZus,v = fPMmax ∙ cS = (fMmax - fSMmax ) ∙ cS = 5 μм ∙ 549 кН/мм = 2,8 кН
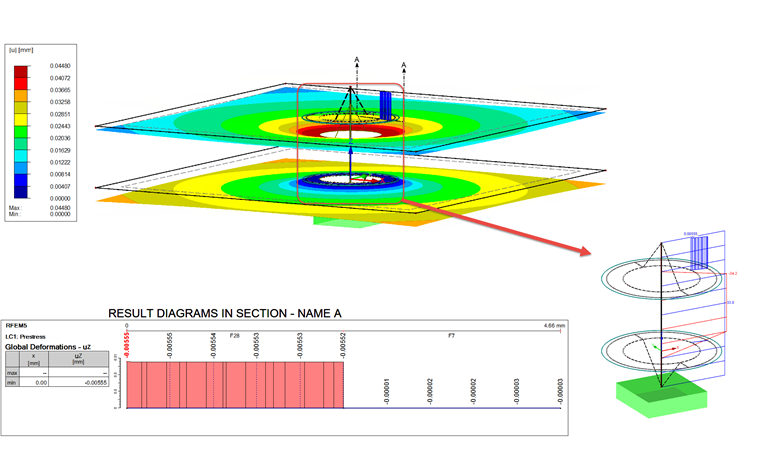
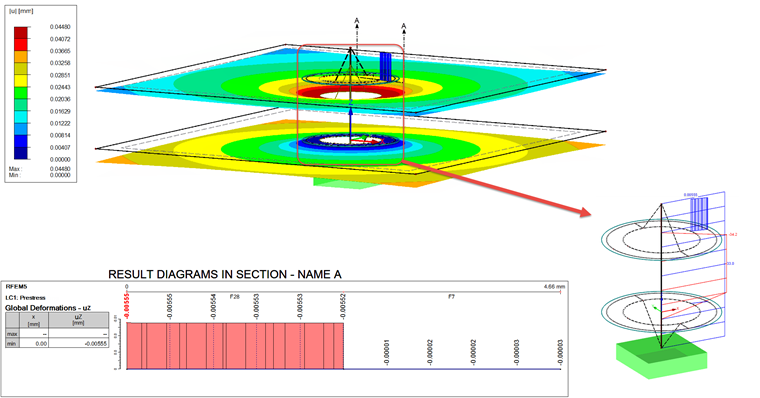
Итеративную дополнительную силу FZus,i можно получить после расчета нагружения на стержне, показанном на рисунке 07.
FZus,i = 33,2 кН - 30,4 кН = 2,8 кН
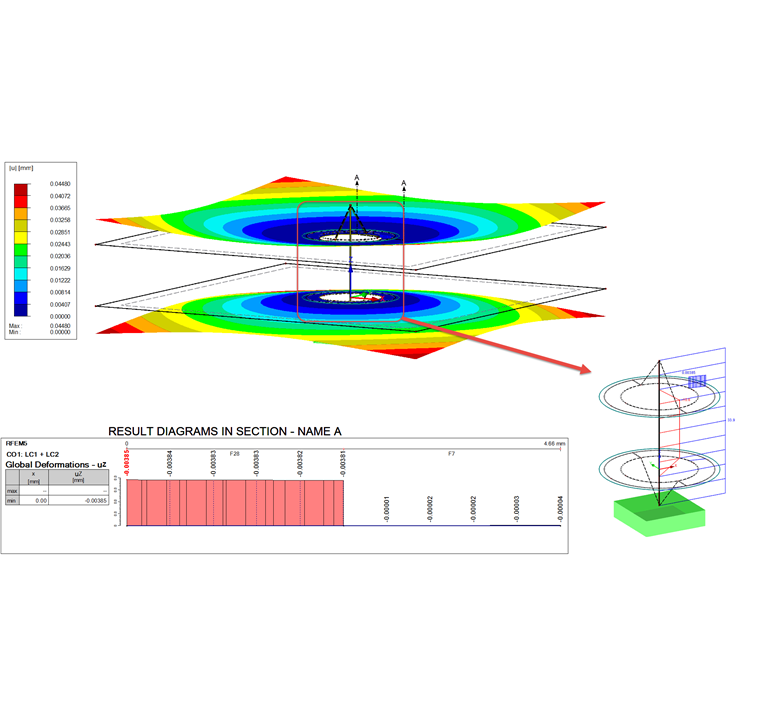
Таким образом, результирующее предварительное напряжение в обоих случаях составляет 36 кН. Это позволяет пересчитать загружение. Результат показан на рисунке 08.
Дополнительный результирующий стержень, который суммирует контактные силы всех контактных тел, имеет результат 34,2 кН. Это примерно на 1,2 кН больше, чем осевая сила стержня, которая составляет 33 кН. Деформацию обеих поверхностей (S1 и S27), показанную на диаграмме, нужно сложить, чтобы можно было сравнить ее с fPMmax. В среднем это приводит к следующему:
Таким образом, деформация на 0,6 мм больше, чем расчетная деформация fMmax.
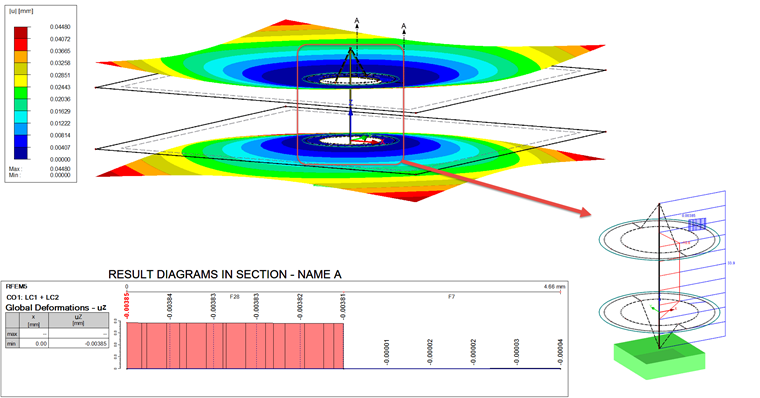
Результат расчетов с учетом рабочей нагрузки в ЗГ1 показан на рисунке 09.
Болтовой стержень имеет результат 33,9 кН. Данную силу на стержень можно сравнить с силой FSmax = 35 кН (см. таблицы 1 и 3, Рабочая нагрузка). Разница составляет 1,1 кН. Здесь также важно отклонение разностей. Согласно аналитическому расчету разница должна быть равна силе FSA = 1,8 кН. Тем не менее, разница лишь в два раза меньше, и составляет 33,9 кН - 33 кН = 0,9 кН.
Аналогичные отклонения мы получим в случае деформации (диаграмму можно найти на рисунке 09). Указанное значение является значением, уменьшенным от рабочей нагрузки. Таким образом, деформация должна быть рассчитана от рабочей нагрузки через деформацию от предварительного напряжения. Фактическая деформация - это разница между uz,1 и средней деформацией на диаграмме. Аналитическое исходное значение - fSA. В результате мы получим деформацию uz,2 :
Таким образом, деформация примерно на 1,4 микрона меньше, чем расчетная деформация fMmax.
Наконец, результаты в результирующем стержне сравниваются. Как видно на рисунке 09, нагрузкой для результирующего стержня является сжимающая сила, равная 10,6 кН. Это значение необходимо сравнить с нагрузкой смыкания FK = 10 кН. В результате мы получим отклонение размером 0,6 кН. В таблице 4 содержится сводка всех результатов.
| Символ | Аналитический Значение | Расчет МКЭ | Отклонение | |
|---|---|---|---|---|
| Стержень | Пластина | |||
| FMmax [кН] | 33,2 | 33,0 | 34,2 | 0,2/1,2 |
| fPMmax [мкм] | 5,0 | - | 5.6 | 0,6 |
| fSA [мкм] | 3.0 | - | 1.6 | 1.4 |
| FMmax + FSA [кН] | 35,0 | 33,9 | - | 1.1 |
| FMmax - FPA [кН] | 10,0 | - | 10,6 | 0,6 |
Таблица 4 - Сравнительные значения аналитической модели и расчета по МКЭ
Оценка
Как показано в таблице 4, между отдельными моделями имеются значительные различия. Как правило, наибольшие совпадения находятся в загружении предварительного напряжения. В зависимости от оценки результирующего стержня (плиты) или болта, отклонения от FMmax составляют 3,6 % или 0,6 % (относительно аналитического результата).
Самым большим отклонением является результат болтового стержня и деформации плиты после приложения рабочей нагрузки. В этом случае между нормальной силой на стержне и аналитическим решением возникает отклонение на 1,1 кН. Данное отклонение относительно аналитического решения первоначально составляет 3%. При этом разница гораздо заметнее, когда речь идет о дополнительной силе болта. Отклонение модели МКЭ составляет:
FSA,FEM = (FMmax + FSA ) - FMmax = 33,9 кН - 33 кН = 0,9 кН < 1,8 кН = FSA
Данные отклонения могут быть вызваны тем, что обе пластины не имеют жесткости в направлении z, а контактное тело имеет в своей толщине только один элемент КЭ. Таким образом, в теле не может быть расширения нагрузки. Передача нагрузки в твердом теле осуществляется исключительно через деформацию плиты под действием изгиба и поперечной силы. Из значений видно, что модель КЭ в случае Преднапряжения в комбинации пластин и контактных тел имеет меньшую жесткость, чем в аналитической модели (см. меньшую деформацию). На данном этапе можно исключить более высокую жесткость болта, так как она определяется теорией балки и сечением.
С другой стороны, в случае сочетания нагрузок в модели МКЭ возникает меньшая деформация, или сила болта имеет значительно меньшее приращение. Это также указывает на более высокую жесткость плиты. Таким образом, есть только одно объяснение этому: Составная часть пластины и контактных тел имеет различное расширение нагрузки, поэтому подход по формуле 3.2 в модели МКЭ недействителен. Чтобы узнать, какое решение ближе к реальности, скорее всего, будет необходимо изучить реальный пример или расширенную модель МКЭ.
При этом важно иметь в виду следующее: Остаточная зажимная сила в обоих вариантах почти одинакова. Таким образом, предварительное напряжение в соединении будет хорошо смоделировано и может быть использовано для расчета соединений.
Заключение
Моделирование преднапряженных болтовых соединений с помощью контактных тел, поверхностей и балок - это сочетание практического решения и реального отображения. Практический означает, что время вычисления значительно меньше по сравнению с расчетом с тел МКЭ, что, возможно, более точно отображает соединение. Тем не менее, будет необходимо улучшить расчет болтов или выполнить дополнительный анализ, который приведет результаты в соответствие с реальностью.
Поскольку силы предварительного нагружения и остаточные силы защемления в основном соответствуют значениям из аналитического расчета, можно предположить, что данный тип моделирования можно применить для расчета соединения.