Modelowanie sprężonego połączenia śrubowego

Wykresy połączeń - podstawy

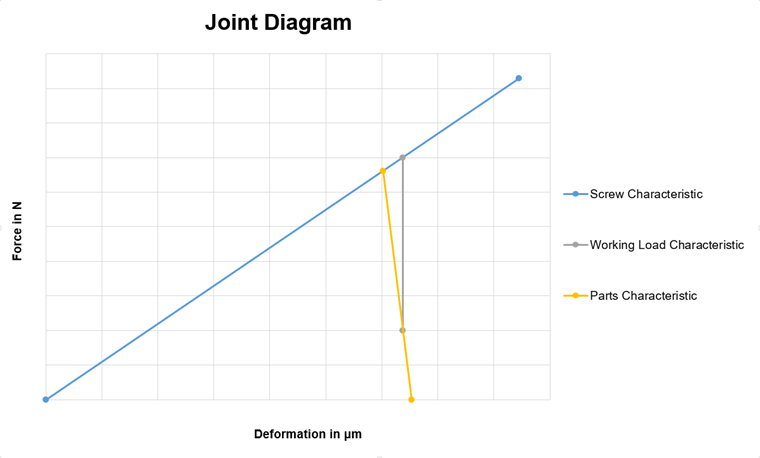
Wykres połączeń jest graficzną reprezentacją sił w sprężonym połączeniu śrubowym. W tym przypadku siły ściskające powstające w łączonych elementach i związane z tym odkształcenia są porównywane z siłami i odkształceniami w śrubie. Rysunek 01 przedstawia taki wykres.

Niebieska linia (linia charakterystyczna) przedstawia wykres śruby, a żółta - wykres poszczególnych elementów konstrukcyjnych. Zazwyczaj sztywność śruby jest mniejsza niż sztywność elementów konstrukcyjnych. Istnieją jednak również różne wyjątki, takie jak w przypadku nakrętek. Przecięcie obu linii przedstawia siłę obciążenia wstępnego w połączeniu bez przyłożonego obciążenia zewnętrznego. Punktem końcowym linii śrub jest maksymalna siła nośności w gwincie.

Oprócz linii śrub i linii składowych istnieje inna ważna linia charakterystyczna zewnętrznej siły rozciągającej (również napięcia wstępnego). Linia ta jest zaznaczona na szaro na rysunku 01. Wychodzi ona z linii charakterystycznej elementów na osi y żądanej resztkowej siły mocującej. Resztkowa siła mocująca to siła, która nadal utrzymuje elementy razem. Na przykład, jeżeli oprócz obciążenia rozciąganego w przypadku istniejącego obciążenia roboczego dodatkowo istnieje siła pozioma, która ma zostać przeniesiona przez połączenie (bez odkształceń ścinających śruby, a więc tylko poprzez tarcie składowe), wówczas resztkowa siła zaciskowa należy wybrać w taki sposób, aby zapewnić odpowiednią nośność.

Oprócz tych linii charakterystycznych dostępne są inne linie, które można wykorzystać do bardziej szczegółowego odwzorowania. Ponieważ jednak linie te nie mają wpływu na podstawowy sposób postępowania, nie będą one omawiane w dalszej części artykułu, a przedstawiony uproszczony schemat połączeń zostanie wykorzystany jedynie. Na przykład, dodatkowe linie charakterystyczne byłyby wynikiem zbioru ściskanego lub naprężenia mimośrodowego i obciążenia.

Wzory uproszczonego wykresu połączenia

Aby utworzyć wykres połączeń, należy najpierw obliczyć odpowiednie sztywności, odkształcenia i siły. Sztywności sprężyste można obliczyć zgodnie z prawem Hooke'a w następujący sposób:

gdzie
c sztywność (stała sprężystości),
F jest siłą sprężyny,
f odkształcenie (ugięcie).

W przypadku pręta rozciąganego z materiału izotropowego, stałą sprężystości można obliczyć bezpośrednio za pomocą modułu sprężystości:

gdzie
E jest modułem sprężystości,
A jest polem przekroju pręta rozciąganego,
l jest długością pręta rozciąganego.

Sztywność śruby jest uproszczona i stosowany jest tylko trzpień śruby. Inne opcje to zastosowanie łba śruby, gwintu, nakrętki, różnych średnic trzonu itp. W takim przypadku elementy wraz z ich odwrotną wartością są dodawane do sztywności całkowitej. Sztywność sprężysta śruby obliczana jest według następującego wzoru (indeks S):

gdzie
c_S jest sztywnością sprężystą śruby,
E_S moduł sprężystości śruby,
A_S jest polem przekroju śruby,
l_K to długość zamocowania (wysokość/grubość elementów).

Średnica boku gwintu d₃ jest stosowana jako pole przekroju w obszarze gwintu śruby. Formuła sumaryczna daje zatem następujące wyniki:

W podobny sposób obliczana jest sztywność elementu. Ponieważ istnieje jedna płyta lub więcej, stosuje się indeks P:

gdzie
c_P sztywność sprężysta elementów/płyt,
E_P moduł sprężystości płyt,
A_P jest polem przekroju płyt,
l_K to długość zamocowania (wysokość/grubość elementów).

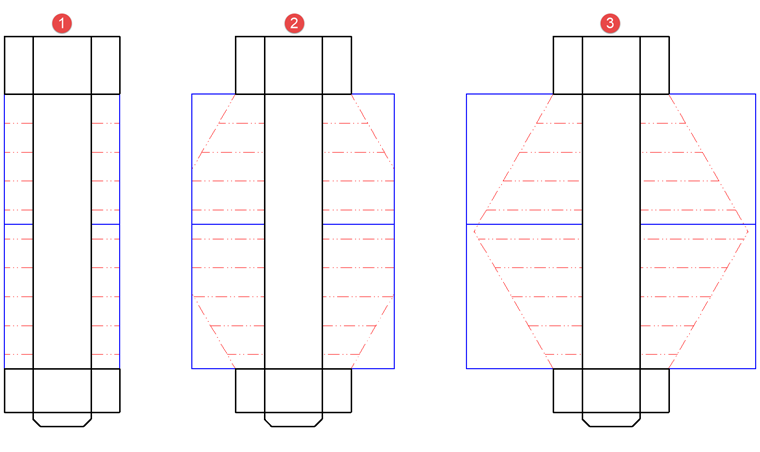
Pole przekroju A_P w przeciwieństwie do śruby zależy od grubości. Przyjmuje się, że obciążenie rozciąga się pod kątem około 60°. Istnieją trzy różne przypadki, jak pokazano na rysunku 02.

W przypadku 1 części między śrubą a nakrętką są jak tuleja, a średnica tulei jest maksymalnie równa średnicy powierzchni nośnej śruby lub nakrętki.
Przypadek 2 obejmuje zakres, w którym średnica tulei jest minimalnie równa średnicy powierzchni nośnej nakrętki lub śruby i maksymalnie równa średnicy stożka przenoszenia obciążenia (zaznaczona na czerwono na rysunku 02). Rozciąga się on symetrycznie z obu stron, a średnica jest największa w środku długości mocowania.
Przypadek 3 obejmuje zakres od maksymalnego obciążenia wydłużenia stożka do nieskończonego wydłużenia płyty. Z tego względu konieczne jest obliczenie pola wymiany A_ers. A_ers odpowiada polu przekroju zastępczego cylindra przy stałym wydłużeniu obciążenia.

W poniższym przykładzie wystarczający jest przypadek 3. A_er oblicza się według następującego wzoru (patrz VDI 2230, wydanie 1986 [1] ):

gdzie
d_W średnica powierzchni nośnej,
d_h jest średnicą otworu.

Średnicę powierzchni podparcia można przyjąć w sposób uproszczony jako 90% szerokości w poprzek płaszczyzny:
d_W = 0,9 ∙ s (3.3)
gdzie
s jest szerokością klucza łba/nakrętki śruby.

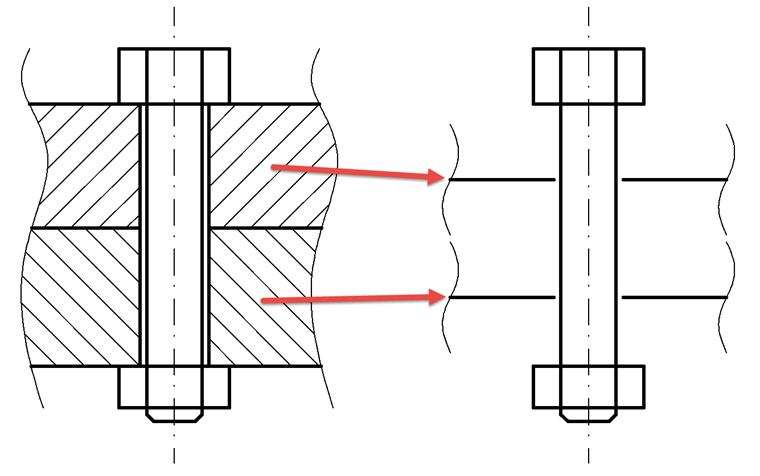
Ponieważ punkt przyłożenia obciążenia w modelu powierzchniowym niekoniecznie znajduje się w górnej części elementu (płyty), lecz zawsze w środku powierzchni, w tym punkcie przyłożenia obciążenia należy określić sztywność płyty. W tym celu wprowadzany jest współczynnik przyłożenia obciążenia n, który odpowiednio zmniejsza długość mocowania. Problem ten zilustrowano na rysunku 03.

Właściwe elementy (w tym przypadku dwie płyty) są zredukowane do środka powierzchni. W przypadku dwóch płyt n wynosi zawsze 0,5, ponieważ zawsze używana jest połowa każdej płyty. Nowa sztywność płyty c_Pn jest obliczana w następujący sposób:

gdzie
Φ_K jest stosunkiem obciążenia.

Aby utworzyć linie charakterystyczne, oprócz sztywności, nadal potrzebne są różne siły. Należy określić resztkowe obciążenie zaciskające F_KR, obciążenie robocze F_A oraz współczynnik dokręcania α_A (dokręcanie kontrolowane kątem). Należy natomiast obliczyć wypadkowe minimalne i maksymalne siły montażowe F_Mmin i F_Mmax. Poniżej znajduje się wzór na naprężenia wstępne zespołu przy dokręcaniu pod kątem kontrolowanym:
F_Mmin = F_Kmin + F_PA (3.6)
F_Mmax = α_A ∙ F_Mmin (3.7)
gdzie
α_A jest współczynnikiem dokręcenia dla metody kontrolowanego kąta,
F_Kmin jest minimalną wymaganą resztkową siłą zacisku w połączeniu,
F_PA jest dodatkowym obciążeniem płytą, wynikającym z obciążenia roboczego.

Dodatkowe obciążenie płytą F_PA jest siłą powstającą podczas przyłożenia obciążenia roboczego. Obliczany jest według wzoru:
_FPA = (1 - n ∙ Φ_K ) ∙ F_A (3.8)
gdzie
F_A jest obciążeniem roboczym.

Upraszczając bez uwzględnienia osiadań, siła sprężająca F_V odpowiada minimalnej sile sprężającej F_Mmin. Aby uwzględnić linię obciążenia roboczego, pominięto maksymalną siłę w śrubie F_Smax, która powstaje w śrubie po uwzględnieniu obciążenia roboczego:
F_Smaks. = F_Mmaks. +_FSA (3.9)
gdzie
F_SA jest dodatkową siłą w śrubie.

Dodatkową siłę w śrubie F_SA oblicza się w sposób podobny do wzoru 3.8:
_FSA = n_K F_A (3.10)

Maksymalną nośność śruby (F_0.2 ) jako ostatnią brakującą siłę należy określić na podstawie pola przekroju śruby w gwincie. Jest to obliczane na podstawie średnicy pola przekroju d_s, która wynika ze średniej wartości średnicy rdzenia d_k (d₃ ) i średnicy boku d_fl (d₂ ):

gdzie
d₂ średnica boku przyłożenia gwintu,
d₃ średnica rdzenia gwintu,
_fub wytrzymałość na rozciąganie materiału śruby.

Oprócz sił należy określić odkształcenia jako odpowiednie wartości, aby można było wprowadzić linie charakterystyczne na wykresie połączeń. W tym celu stosuje się wzór 1.1 przekształcony według f. Poniżej znajdują się wzory na odkształcenia f od odpowiednich sił F:

Skutkuje to następującymi wartościami/punktami linii dla wykresu połączeń:

Charakterystyczna linia	odkształcenie	Siła
Wkręt	0	0
	F0,2	F0,2
Płyta	fSMmax	FMmax
	fSMmax + fPMmax lub fMmax	0
Obciążenie robocze	fSMmax + fSA	FMmax − FPA
	fSMmax + fSA	FMmax + FSA = FSmax

Tabela 1 - Punkty/wartości linii dla wykresu połączeń

Modelowanie sprężonego połączenia śrubowego w RFEM

Model powinien być dobrym połączeniem dokładności i praktyczności. Połączenie będzie składać się z powierzchni, prętów i brył kontaktowych.

Dla przykładu obliczeniowego określone są następujące parametry:
_FA = 25 kN
_FK = 10 kN
E_S = E_P = 210 000 N/mm²
t₁ = t₂ = 10 mm
l_K = t₁ + t₂ = 20 mm
d_h = 10 mm
D_A > d_W + l_K
n = 0,5
α_A = 1,0

Śruba:
M10 8.8
f_ub = 800 N/mm²
_d2 = 9,03 mm
d3₌ 8,16 mm
s = 17 mm

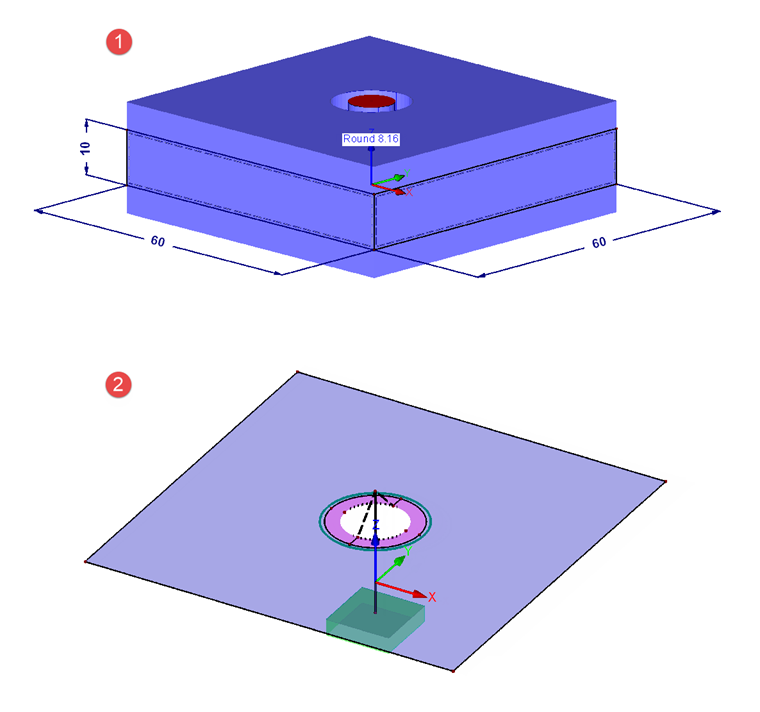
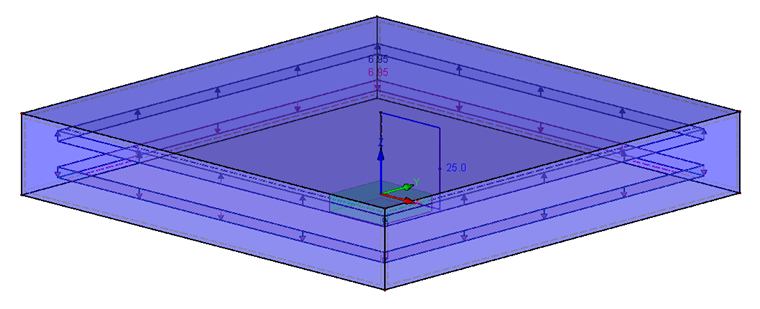
Model zawiera dwie nałożone na siebie kwadratowe powierzchnie z otworem (średnica d_h ) w środku, które mają wymiary 60 x 60 mm (dla wypełnienia D_A > d_W + l_K ). Ponieważ t₁ = t₂, odległość między płytami wynosi 10 mm. Obciążenie działa bezpośrednio na środek płyty (włókno neutralne). Zatem wynikowa wartość n wynosi 0,5. Model jest podparty na nieruchomej podporze na dolnym końcu pręta-śruby. Aby uzyskać całkowitą siłę podporową równą zero, obciążenie musi zostać przyłożone do górnej i dolnej płyty. Obciążenie wynosi 6,95 N/mm² dla 25 kN siły całkowitej.

_W celu zapewnienia dobrego przenoszenia obciążeń między śrubą (belką) a płytami wokół otworu modelowana jest sztywna powierzchnia (pierścień) o średnicy zewnętrznej dW. Połączenie między płytami jest generowane za pomocą trzech brył kontaktowych. Jedna bryła znajduje się wokół otworu bez części typu powierzchnia sztywna; dwie bryły kontaktowe spoczywają wokół otworu jak dwie powłoki. Bryły kontaktowe muszą być wykonane z tego samego materiału co płyty, aby dokładnie odzwierciedlić sztywność między płytami. Ponadto styk ulega zniszczeniu podczas podnoszenia i wykazuje tarcie sztywne w kierunku poziomym o współczynniku 0,1.

Konstrukcja jest wyświetlana na rysunku 04. Numer 1 pokazuje powierzchnie i pręty w rzeczywistych wymiarach. Numer 2 pokazuje górną powierzchnię z belką (śrubą) i prętami sztywnymi, które stanowią połączenie między śrubą a płytą. Sztywna powierzchnia (kolor różowy) ma również sztywny pręt na wewnętrznej krawędzi, który może przenosić dowolne momenty.

Kolejnym ważnym punktem jest siatka ES. Ze względu na małe wymiary główny rozmiar siatki ES dla_lFE został ustawiony na 2 mm. Ponadto na powierzchniach sztywnych zdefiniowano powierzchniowe zagęszczenie siatki za pomocą_lFE 0,2 mm.

Ponieważ w praktyce nie jest znana średnica śruby ani siła robocza działające na śrubę, możliwe jest zamodelowanie konstrukcji bez otworu i zastosowanie pręta sztywnego zamiast belki do pierwszego wymiarowania modelu oraz do określenia siły śrub. Ten model dla wstępnego zwymiarowania pokazano na rysunku 05.

Aby możliwe było wykrycie szczątkowego naprężenia wstępnego w modelu, równolegle do śruby zamocowano pręt wynikowy (odległość 0,1 mm). Obejmuje to wszystkie siły wewnętrzne bryły kontaktowej.

Porównanie rozwiązań analitycznych i numerycznych

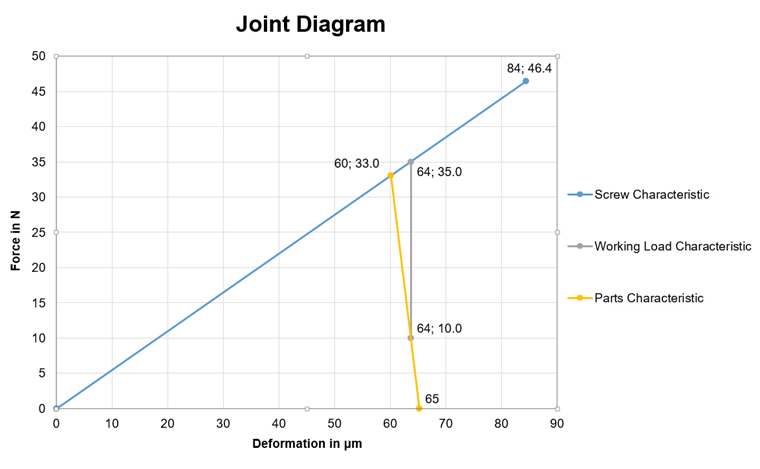
Aby porównać rozwiązania, należy najpierw utworzyć wykres połączeń. Wymagane wartości są podane w tabeli 1. Wartości pośrednie i linie charakterystyczne przedstawione w tabeli 2 uzyskuje się poprzez podstawienie tych wartości do przykładu praktycznego (patrz wyżej). Analogicznie jak w tabeli 1, w tabeli 3 znajduje się zestawienie najważniejszych wartości, a rysunek 06 przedstawia kompletny wykres połączeń.

Symbol	Numer wzoru	Wartość
Cs	2,2	549 kN/mm
Aers	3.2	303 mm²
CP	3,1	3182 kN/mm
ΦK	3,5	0,147
CPn	3,4	6,921 kN/mm
FAS	3.10	1,8 kN
FAS	4.4	3 μm
FPA	3.8	23,2 kN
FMmax	3.6, 3.7	33,2 kN
fSMmax	4.2	60 μm
FMmax	4.3	65 μm
F0,2	3,11	46,2 kN
F0,2	4.1	84 μm

Tabela 2 - Wyniki pośrednie i wyniki obliczeń przykładowych

Charakterystyczna linia	Odkształcenie [μm]	Siła [kN]
Wkręt	0	0,0
	84	46,2
Płyta	60	33,2
	65	33,2
Obciążenie robocze	63	10.0
	63	35,0

Tabela 3 - Punkty charakterystyczne linii/wartości z przykładu obliczeń

Początkowo, dla rozwiązania numerycznego utworzono dwa przypadki obciążeń. Pierwszy przypadek obciążenia (PO1) sprężenie obejmuje obciążenie prętowe wynikające z sprężenia, a drugi przypadek (PO2) Obciążenie robocze obejmuje obciążenie robocze. Ponadto wygenerowano kombinację obciążeń dla obu przypadków obciążeń (współczynnik 1.0) (KO1: PO1 + PO2). Obliczenia opierają się na liniowej analizie statycznej z 15 krokami obciążenia (lepsza zbieżność w przypadku brył kontaktowych z uszkodzeniem).

W przypadku sprężenia można zastosować do pręta sprężenie początkowe lub sprężenie końcowe. Rzeczywiste obciążenie wstępne jest naprężeniem końcowym. Ponieważ obciążenie naprężeniami końcowymi jest czasochłonne, zaleca się stosowanie wstępnego naprężenia prętowego. Ma to jednak tę wadę, że obciążenie to nie obejmuje siły reakcji przechodzącej przez płyty. Z tego względu siła osiowa w pręcie jest po obliczeniach zbyt mała, ponieważ część można zredukować poprzez odkształcenie płyt. Różnicę tę można zmniejszyć na dwa sposoby. Można to z jednej strony przewidzieć na podstawie odkształcenia płyty i przeliczyć na dodatkową siłę F_{Zus, v} (przewidywaną) według następującego wzoru:
F_{Zus, v} = f_PMmax ∙ c_S (5.1)

Z drugiej strony można to również określić iteracyjnie. W tym celu należy obliczyć przypadek obciążenia naprężającego. Różnica między założonym początkowym naprężeniem wstępnym a wypadkową siłą osiową w pręcie odpowiada dodatkowej sile F_zus,i (iteracyjnie). Można użyć następującego wzoru:
F_{Zus, i} = F_Mmax - N_S (5.2)
gdzie
N_S siła osiowa w pręcie przy początkowym naprężeniu wstępnym F_Mmax.

Dodatkowa siła_FZus,v wynika z wartości w tabeli 2 w następujący sposób:
F_{Zus, v} = f_PMmax ∙ c_S = (f_Mmax - f_SMmax ) ∙ c_S = 5 μm ∙ 549 kN/mm = 2.8 kN

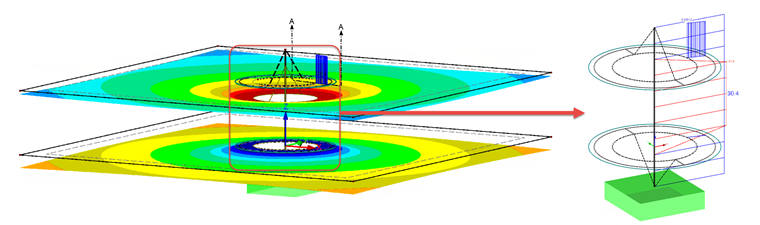
Dodatkową siłę iteracyjną_FZus,i można uzyskać po obliczeniu przypadku obciążenia na pręcie na rysunku 07.

F_Zus,i = 33,2 kN - 30,4 kN = 2,8 kN

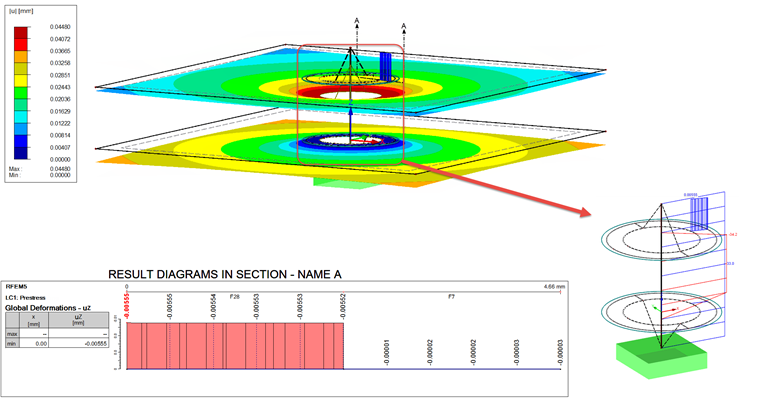
Zatem w obu przypadkach końcowe naprężenie wstępne wynosi 36 kN. Pozwala to na ponowne obliczenie przypadku obciążenia. Wynik pokazano na rysunku 08.

Dodatkowy pręt wynikowy sumujący siły kontaktowe wszystkich brył kontaktowych daje wynik 34,2 kN. Jest to o około 1,2 kN więcej niż siła osiowa śruby, która wynosi 33 kN. Odkształcenie obu powierzchni (S1 i S27) pokazane na wykresie należy dodać, aby możliwe było porównanie go z f_PMmax. Wynika to średnio następująco:

Odkształcenie jest zatem o 0,6 μm większe niż obliczone odkształcenie f_Mmax.

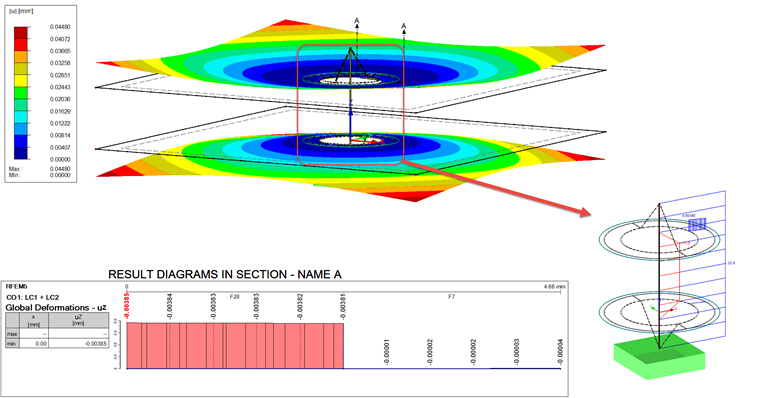
Wynik obliczeń poddany obciążeniu roboczemu w PO1 pokazano na rysunku 09.

Pręt-śruba ma wynik 33,9 kN. Siłę tę można porównać z siłą F_Smax = 35 kN (patrz Tabela 1 i Tabela 3, Obciążenie robocze). Różnica wynosi 1,1 kN. Istotna jest tu również odchyłka różnic. Zgodnie z obliczeniami analitycznymi różnica powinna być równa sile F_SA = 1,8 kN. Jednak różnica w stosunku do modelu ES jest tylko o połowę mniejsza i wynosi 33,9 kN − 33 kN = 0,9 kN.

Podobne odchylenia uzyskuje się w przypadku odkształcenia (patrz wykres na rys. 09). Wyświetlana wartość jest wartością pomniejszoną o obciążenie robocze. Odkształcenie należy zatem obliczyć na podstawie obciążenia roboczego z wykorzystaniem odkształcenia wywołanego sprężeniem. Rzeczywiste odkształcenie jest różnicą między u_z,1 a średnim odkształceniem na wykresie. Analityczną wartością odniesienia jest f_SA. Skutkuje to deformacją u_z,2 :

Tym samym odkształcenie jest o około 1,4 μm mniejsze niż obliczone odkształcenie f_Mmax.

Na koniec porównywane są wyniki w pręcie wynikowym. Jak widać na rysunku 09, obciążenie dla pręta wynikowego to siła ściskająca 10,6 kN. Wartość tę należy porównać z siłą zacisku F_K = 10 kN. Skutkuje to odchyłką 0,6 kN. Tabela 4 zawiera zestawienie wszystkich wyników.

Symbol	Analityczny Wartość	Obliczenia MES		odchylenie
		Pręt	Płyta
FMmax [kN]	33,2	33,0	34,2	0,2/1,2
fPMmax [μm]	5.0	-	5.6	0.6
fSA [μm]	3,0	-	1,6	1,4
FMmax + FSA [kN]	35,0	33,9	-	1,1
FMmax - FPA [kN]	10.0	-	10,6	0.6

Tabela 4 - Wartości porównawcze modelu analitycznego/obliczeń MES

Ocena

Jak pokazano w tabeli 4, między modelami występują częściowo duże różnice. Zazwyczaj największe dopasowania występują w przypadku obciążenia sprężenie. W zależności od oceny pręta wynikowego (płyty) lub śruby odchyłki od F_Mmax wynoszą 3,6% lub 0,6% (w odniesieniu do wyniku analitycznego).

Największa odchyłka jest wynikiem odkształcenia śruby i płyty po przyłożeniu obciążenia roboczego. W tym przypadku odchyłka między siłą osiową na pręcie a rozwiązaniem analitycznym wynosi 1,1 kN. Odchylenie to, w odniesieniu do rozwiązania analitycznego, wynosi początkowo 3%. Różnica jest jednak znacznie większa w odniesieniu do dodatkowej siły w śrubie. Odchylenie modelu MES jest następujące:
_FSA,FEM = (F_Mmax + F_SA ) - F_Mmax = 33,9 kN - 33 kN = 0,9 kN << 1,8 kN =_FSA

Odchylenia te mogą być spowodowane tym, że obie płyty nie mają sztywności w kierunku z, a grubość bryły kontaktowej jest tylko jeden element skończony. Dzięki temu w bryle nie może wystąpić wydłużenie obciążenia. Przenoszenie obciążenia w bryle odbywa się wyłącznie poprzez odkształcenie płyty poprzez zginanie i siłę tnącą. Z tych wartości jasno wynika, że model ES w przypadku obciążenia sprężeniem w kombinacji płyt i brył kontaktowych ma mniejszą sztywność niż w modelu analitycznym (patrz mniejsze odkształcenie). Na tym etapie można wykluczyć większą sztywność śruby, ponieważ jest to określone przez teorię belki i przekroju.

Z drugiej strony, w przypadku kombinacji obciążeń w modelu MES odkształcenie jest mniejsze lub siła w śrubach ma znacznie mniejszy przyrost. To ponownie wskazuje na większą sztywność płyty. Podsumowując, jest tylko jedno wytłumaczenie: Połączenie płyty i bryły kontaktowej ma różne wydłużenie obciążenia, dlatego podejście ze wzoru 3.2 w modelu MES nie jest prawidłowe w tej postaci. Aby dowiedzieć się, które rozwiązanie jest bliższe rzeczywistości, konieczne byłoby przeanalizowanie rzeczywistego przykładu lub rozszerzonego modelu MES.

Należy jednak pamiętać, że: Pozostała siła mocująca jest prawie identyczna w obu wariantach. Dzięki temu naprężenie wstępne w połączeniu jest dobrze zamodelowane i może być wykorzystane do analizy połączenia.

Podsumowanie

Modelowanie sprężonego połączenia śrubowego za pomocą brył kontaktowych, powierzchni i belek jest połączeniem praktycznego rozwiązania z rzeczywistym odwzorowaniem wyników. Praktyczny oznacza, że czas obliczeń jest znacznie krótszy w porównaniu z obliczeniami z wykorzystaniem brył MES, które prawdopodobnie dokładniej odwzorują połączenie. Konieczne jest jednak ulepszenie projektowania śrub lub przeprowadzenie dalszej analizy, w której wyniki zostaną odniesione do rzeczywistości.

Ponieważ siły napięcia wstępnego i resztkowe siły mocujące w dużej mierze odpowiadają wartościom uzyskanym w obliczeniach analitycznych, można założyć, że ten sposób modelowania można wykorzystać do analizy połączeń.

Literatura

[1]	Stowarzyszenie Inżynierów Niemieckich: (1986). Wytyczna VDI 2230 – Systematyczne obliczanie połączeń śrubowych poddawanych dużym obciążeniom. Berlin: Beuth.