返回知识库

14806x

001499

Dipl.-Ing. Thomas Günthel

2017-12-26

Modelling Prestressed Bolt Connection

在对面的模型例如框架节点或类似结构进行建模时，总是会出现如何建模预应力螺栓连接的问题。在这种情况下，就必须总是在可行和详细的解决方案之间找到一个折衷的方法。下面根据节点图计算方法介绍这种连接的建模过程。

节点图表基本

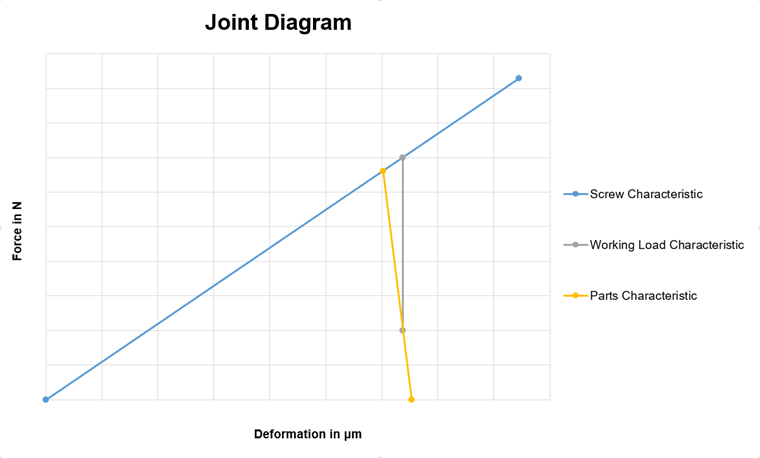
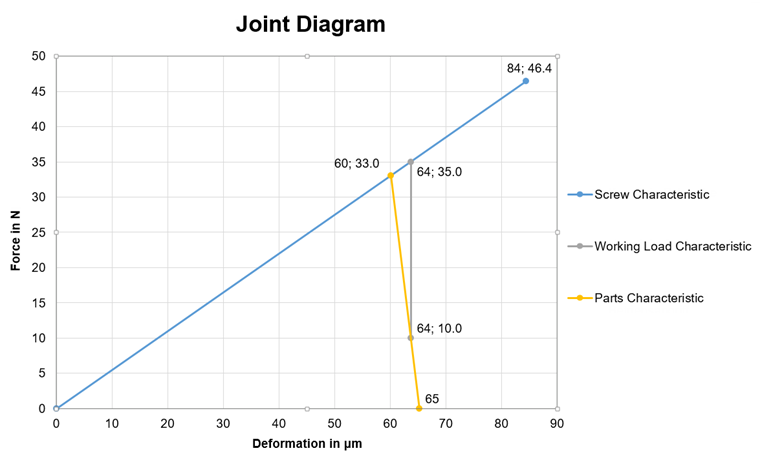
节点图是预应力螺栓连接中力的图形表示。在这种情况下，待连接组件中产生的压力和变形与螺栓的力和变形形成对比。图01显示了这样的图。

简化的支撑三角形

蓝色的线（特征线）表示螺栓，黄色的表示结构构件。通常，螺栓刚度小于结构构件的刚度。但是，也有各种例外情况，例如螺母。两条线的交点表示没有施加外部荷载时连接中的预应力。该线的末端点是螺纹中最大阻力的点。

除了螺栓线和分力线外，还有另一条重要的外部拉力特征线。该线在图片01中显示为灰色。 y 轴上的期望残余夹紧力以部件的特征线为起点。残余夹紧力是指仍将组件固定在一起的力。例如，如果除了拉力外还有一个水平分力，并且在现有工作荷载作用下通过连接承受并且必须选择具有足够阻力的截面。

除了这些特征线外，还可以使用其他线来进行更精细的建模。因为这些线对基本操作步骤没有影响，所以在此省略说明，这里只展示简化的节点图。例如，附加特征线是由压缩永久变形或偏心应力和荷载引起的。

简化的节点图公式

要创建节点图表，首先必须要计算相应的刚度、变形和力。通常，根据胡克定律可以计算弹簧刚度，

c = \frac{F}{f} (1.1)

公式 1

有
c 是刚度（弹簧常数），
F 是弹簧力，
f 是变形（挠度）。

材料为各向同性受拉杆件时，弹簧常数可以直接通过弹性模量（弹性模量）计算得出：

c = \frac{E \cdot A}{l} (1.2)

公式 2

有
E 是弹性模量，
A是受拉杆件的截面面积，
l 是受拉杆件的长度

这里简化了螺栓刚度，只在螺栓轴端施加了荷载。其他选项包括应用螺栓头、螺纹、螺母、不同的轴径等。刚度类型中刚度的倒数螺栓的弹簧刚度通过以下公式计算（索引S）：

c_{S} = \frac{E_{S} \cdot A_{S}}{l_{K}} (2.1)

公式 3

有
c_S是螺栓的弹簧刚度，
E_S是螺栓的弹性模量，
A_S是螺栓的截面面积，
l_K是夹紧长度（构件的高度/厚度）

螺纹侧面直径 d₃用于定义螺栓螺纹范围中的截面区域。因此，总的公式得出：

c_{S} = \frac{E_{S} \cdot π}{4} \cdot \frac{d_{3} ²}{l_{K}} (2.2)

公式 4

构件刚度的计算方法类似。因为有一个或多个板，所以使用指数 P：

c_{P} = \frac{E_{P} \cdot A_{P}}{l_{K}} (3.1)

公式 5

有
c_P是构件的弹簧刚度，
E_P板的弹性模量，
A_P是板的截面面积，
l_K是夹紧长度（构件的高度/厚度）

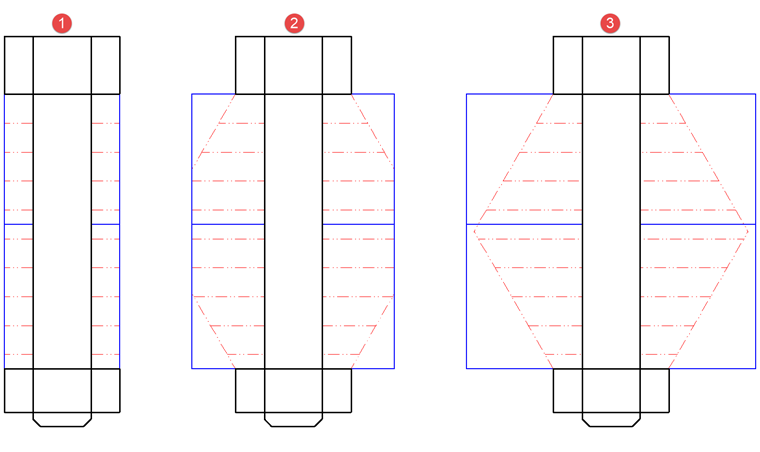
与螺栓不同，截面面积 A_P取决于厚度。假设荷载大约倾斜 60°。如图02所示，存在三种不同的情况。

在不同板尺寸上的荷载传递

工况 1 中，螺栓和螺帽之间的结构像一个套筒，套筒的直径最大等于螺栓或螺帽的支承面直径。
在工况 2 中，套筒直径最小值等于螺栓或螺栓的支承面直径，最大等于荷载延伸圆锥的直径（图 02 中红色标记）。预应力铰从两侧对称延伸，在夹紧长度的中间部分直径最大。
工况 3 涵盖了从最大荷载延伸圆锥到板无限延伸。因此必须重新计算恢复截面的面积 A_ers 。 A_ers相当于替代圆柱的截面面积，其荷载扩展恒定。

对于以下示例，工况 3 就足够了。 A_ers按下式计算（见规范 VDI 2230，1986 [1]版）：

A_{ers} = \frac{π}{4} \cdot (d_{W} ² - d_{h} ²) \frac{π}{8} \cdot d_{W} \cdot l_{K} \cdot ({(\sqrt[3]{\frac{l_{K} \cdot d_{W}}{(l_{K} d_{W}) ²}} 1)}^{2} - 1) (3.2)

公式 6

有
d_W是支承面直径，
d_h是内孔直径。

支承面的直径可以简化为 90% 的两面宽度：
d_W = 0.9 ∙ s (3.3)
有
s 是螺栓头/螺帽的对边宽度。

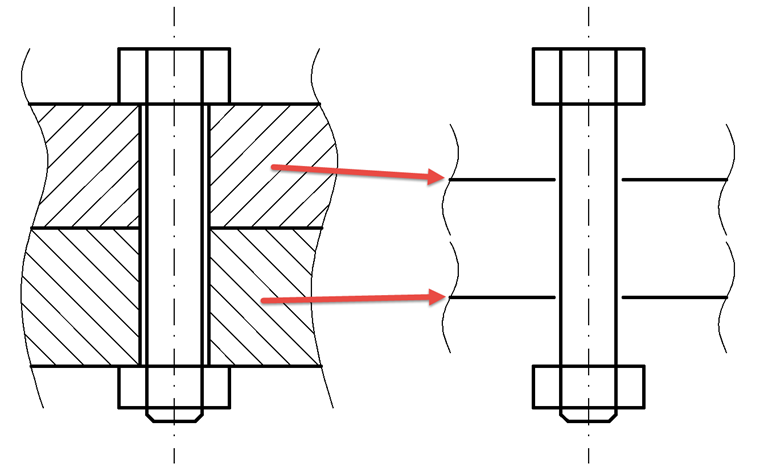
因为在面模型中荷载作用的点不一定在构件（板）的上部，而是在面的中间，所以确定在该点上的板的刚度。为此引入荷载系数 n，它相应地减小了夹持长度。如图03所示。

Umwandlung von Platten-Volumenmodell zu Platten-Flächenmodell

网格划分为两个实际构件（在本例中为两块板）。在有两块板的情况下，n 始终为 0.5，因为每块板总是使用一半。新的板刚度 c_Pn计算如下：

\begin{array}{l} c_{Pn} = c_{S} \cdot \frac{1 - n \cdot Φ_{K}}{n \cdot Φ_{K}} (3.4) \\ Φ_{K} = \frac{c_{S}}{c_{S} c_{P}} (3.5) \end{array}

公式 7

有
Φ_K是荷载比，

为了创建特征线，除了刚度外还需要力。必须指定剩余夹紧荷载 F_KR 、工作荷载 F_A和紧固系数 α_A （角度控制）。但是需要计算由此产生的最小和最大装配内力 F_Mmin和 F_Mmax 。以下是角度受控制的装配预紧的公式：
F_Mmin = F_Kmin + F_PA (3.6)
F_Mmax = α_A ∙ F_Mmin (3.7)
有
α_A是角度控制方法的预应力系数，
F_Kmin是连接中所需的最小残余夹紧力，
F_PA由于工作荷载引起的附加板荷载。

附加板荷载 F_PA是在施加工作荷载时产生的力。计算公式为：
F_PA = (1 - n ∙ Φ_K ) ∙ F_A (3.8)
有
F_A是工作荷载。

在不考虑沉降的简化计算中，预应力 F_V对应于最小预应力 F_Mmin 。考虑工作荷载线，缺少最大螺栓力 F_Smax ，这是在考虑工作荷载时产生的：
F_Smax = F_Mmax + F_SA (3.9)
有
F_SA是附加螺栓力。

螺栓附加力 F_SA的计算方法类似于公式 3.8：
F_SA = n∙ Φ_K ∙ F_A (3.10)

螺栓的最大承载力 (F_0.2 ) 作为最后一个缺失的力必须通过螺栓在螺纹中的截面积来确定。这是根据截面直径d_s计算得出的，d s 是由中心区直径d_k (d₃ )和侧面直径d_fl (d₂ )的平均值得出：

F_{0, 2} = A_{S} \cdot f_{ub} = \frac{π}{4} \cdot {(\frac{d_{2} d_{3}}{2})}^{2} \cdot f_{ub} (3.11)

公式 8

有
d₂是螺纹侧面直径，
d₃是螺纹的内径，
f_ub是螺栓材料的抗拉强度。

除了力外，还必须计算相应的变形值，以便在节点图中输入特征线。公式 1.1 中根据 f 进行了换算。下面是变形 f 到相应外力 F 的公式：

\begin{array}{l} F_{0, 2} \to f_{0, 2} = \frac{F_{0, 2}}{c_{S}} (4.1) \\ F_{Mmax} \to f_{SMmax} = \frac{FMmax}{c_{S}} (4.2) \\ F_{Mmax} \to f_{Mmax} = F_{Mmax} \cdot (\frac{1}{c_{Pn}} \frac{1}{c_{S}}) (4.3) \\ F_{SA} \to f_{SA} = f_{PA} = \frac{F_{SA}}{c_{S}} (4.4) \\ F_{Smax} \to f_{Smax} = \frac{F_{Smax}}{c_{S}} (4.5) \end{array}

公式 9

节点图的线旁点/值如下：

特征线	应变	力
螺栓	0	0
螺栓	f_0,2	[F12]_0.2
楼板	f_SMmax	[F7]_Mmax
楼板	f_SMmax + f_PMmax或 f_Mmax	0
工作荷载	f_SMmax + f_SA	F_Mmax − F_PA
工作荷载	f_SMmax + f_SA	F_Mmax + F_SA = F_Smax

表 1 – 节点图的线点/值

在 RFEM 中建模预应力螺栓连接

模型要求精度与实用性相结合。因此，连接将由面、杆件和接触实体组成。

为计算示例指定了以下参数：
F_A = 25 kN
F_K = 10 kN
E_S = E_P = 210 000 N/mm²
t₁ = t₂ = 10 mm
l_K = t₁ + t₂ = 20 mm
d_h = 10mm
D_A > d_W + l_K
n= 0.5
α_A = 1.0

螺栓:
M10 8.8
f_ub = 800 N/mm²
d₂ = 9.03mm
d₃ = 8.16mm
s = 17mm

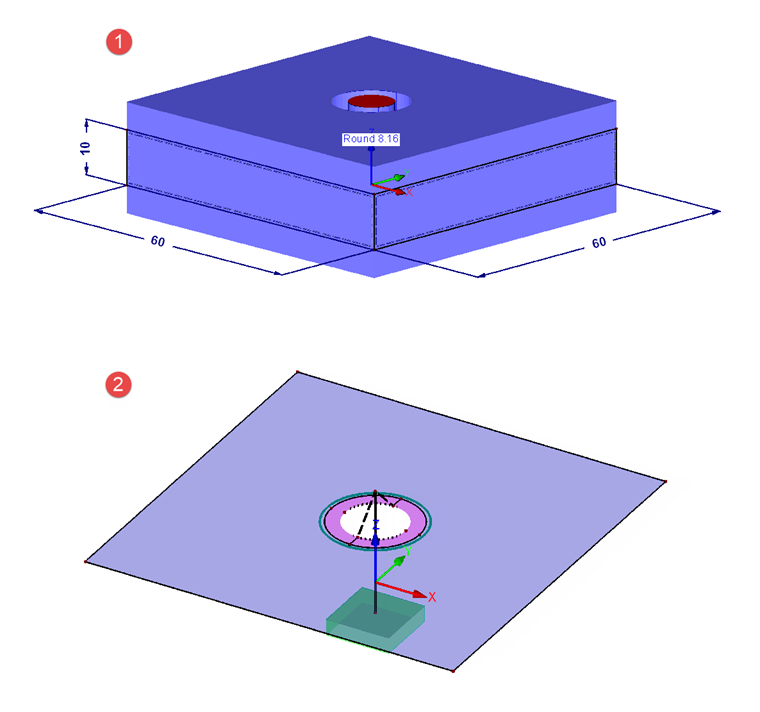
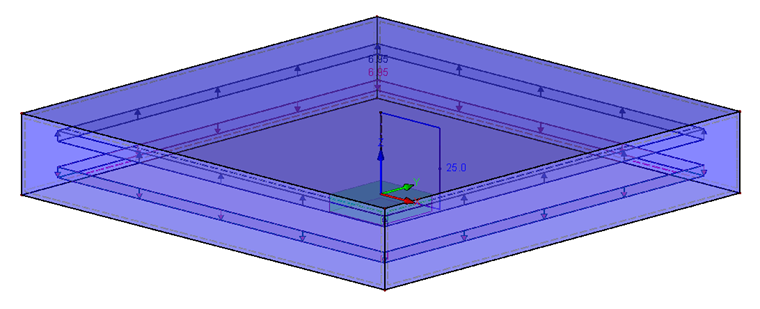
该模型包括两个重叠的正方形面，在中间有一个孔洞（直径 d_h ），尺寸为 60 x 60 mm（满足 D_A > d_W + l_K ）。因为 t₁ = t₂ ，所以板件间距为 10 mm。荷载直接作用在板的中间（中间纤维）。因此 n 等于 0.5。该模型由螺栓杆件底端的固定支座支撑。为了使总的支座反力为零，荷载必须同时施加到上部和下部的板上。荷载为 6.95 N/mm² 总作用力为 25 kN。

为了在螺栓（梁）和板之间实现良好的荷载传递，可以在孔周围建模一个外径为 d_W的刚性面（圆环）。板之间的连接是通过三个接触体生成的。一个实体位于孔洞周围，没有刚性面部分；两个接触实体像两个壳一样围绕孔洞。接触实体必须与板的材料相同，以便准确地反映板之间的刚度。此外，该接触在提升时失效，在水平方向上有一个系数为 0.1 的刚性摩擦。

FEM-Modell der Schraubenverbindung

结构如图04所示。编号1显示具有实际尺寸的面和杆件。编号2显示的是上表面，有梁（螺栓）和刚性杆件，刚性杆件通过螺栓和板之间的连接。刚性面（粉红色）在内部边缘上也有一个刚性杆件，可以传递任何弯矩。

另一个重要的问题是有限元网格。由于尺寸较小，所以有限元网格的主网格尺寸 l_有限元已设置为 2 mm。此外，在刚性面上已经用l_FE 0.2 mm定义了面网格细化。

因为在实际操作中螺栓直径和作用在螺栓上的作用力都是未知的，所以可以模拟没有孔洞的结构，螺栓力。这个预先设定尺寸的模型如图 05 所示。

简化的预尺寸有限元模型

为了能够在模型中检测残余预应力，平行于螺栓放置一个结果杆件（距离 0.1 mm）。包括接触体的所有内力。

解析解与数值比较

为了比较这两种方案，首先需要创建节点图。要求的值列于表1中。表2中所示的中间值和特征线是通过替换实际示例（见上）的值获得的。与表1类似，表3总结了最重要的数值，图06显示了完整的节点图。

符号	公式编号	值
C_{[THESIS.THESISTITLE]}	2.2	549 kN/mm
_热线	3.2	303 平方毫米
C_P	3.1	3182 kN/mm
Φ_K	3.5	0,147
C_Pn	3.4	6.921 kN/mm
[F12]_SA	3.10	1.8 kN
[F12]_SA	4.4	3μm
[F7]_PA	3,8	23.2 千牛
[F7]_Mmax	3.6, 3.7	33.2 千牛顿
f_SMmax	4,2	60 μm
[F12]_Mmax	4.3	65μm
[F12]_0.2	3,11	46.2 千N
f_0,2	4.1	≤84

表 2 – 中间结果和计算示例的结果

特征线	变形 [μm]	力[kN]
螺栓	0	0,0
螺栓	84	46,2
楼板	60	33,2
楼板	65	33,2
工作荷载	63	10.0
工作荷载	63	35,0

表 3 – 计算示例特征线点/值

Vereinfachtes Verspannungsdreieck des Rechenbeispiels

最初创建两个荷载工况进行数值求解。第一个荷载工况（LC1预应力）包括预应力的杆件荷载，第二种荷载工况（LC2工作荷载）包括工作荷载，此外，生成两个荷载工况（系数1.0）的荷载组合（CO1:LC1 + LC2）。该计算基于具有 15 个荷载步的线性静力分析（接触实体具有更好的收敛性）。

预应力可以采用杆件荷载类型初始或末端预应力。实际预应力为末端预应力。由于最终预应力需要花费大量的计算时间，我们建议使用初始预应力的杆件荷载。其缺点是不包含板的反力。因此，计算后杆件的轴力太小，因为部分可以通过板的变形来折减。这种差异可以通过两种方式来缩小。一方面，这可以通过板的变形来预测，并按照下面的公式转换为附加力 F_Zus,v (预测的)：
F Zus_,v = f_PMmax ∙ c_S (5.1)

另一方面，这也可以迭代地确定。首先要计算预应力荷载工况。施加在杆件中的初始预应力和合成轴力之间的差值就是附加力 F_Zus,i （迭代）。可以使用下面的公式：
F_Zus,i = F_Mmax - N_S (5.2)
有
N_S为初始预应力为 F_Mmax时杆件的轴力。

附加力 F_Zus,v由表 2 中数值计算得出:
F Zus_,v = f_PMmax ∙ c_S = (f_Mmax - f_SMmax ) ∙ c_S = 5 μm ∙ 549kN/mm = 2,8 kN

在图 07 中计算了作用在杆件上的荷载工况之后，可以得到迭代附加力 F_Zus,i 。

没有预应力补偿的预应力荷载工况初次计算

F_Zus,i = 33,2 kN - 30,4 kN = 2,8 kN

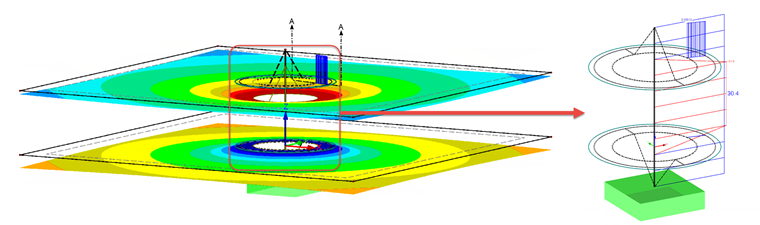
因此，两种情况下产生的预应力都是 36 kN。这样可以重新计算荷载工况。结果如图08所示。

Ergebnisse des Lastfalls Vorspannung

附加的结果杆件将所有接触实体的接触力相加，其结果为 34.2 kN。这比螺栓杆件的轴向力 33 kN 大 1.2 kN。图中所示的两个面 S1 和 S27 的变形必须相加，以便与 f_PMmax进行比较。平均来说，其结果如下：

u_{z, 1} = \frac{0, 00555 0, 00552}{2} \frac{0, 00001 0, 00003}{2} = 5, 6 μm > 5, 0 μm = f_{Mmax}

公式 10

因此，变形比计算出的变形 f_Mmax大0.6 μm。

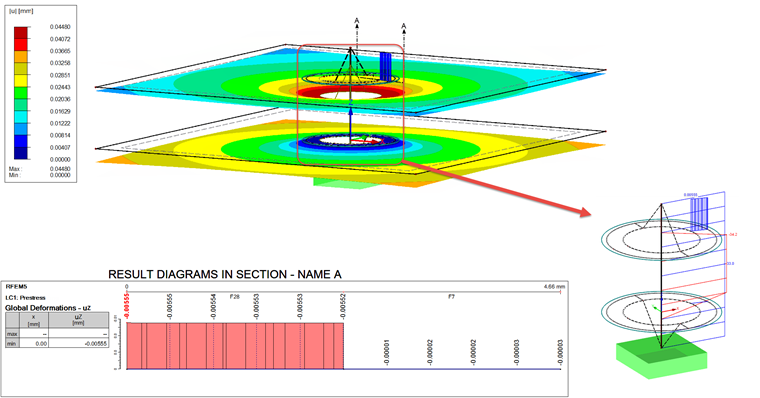
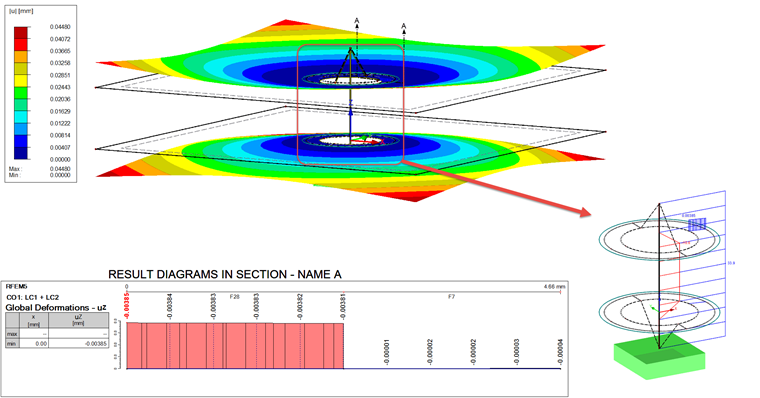
在考虑荷载工况 LC1 时的计算结果如图 09 所示。

Ergebnisse der Lastkombination (Vorspannung und Betriebslast)

螺栓杆件的结果为 33.9 kN。该杆件力可以与力 F_Smax = 35 kN（见表 1和表 3“工作荷载”）进行比较。扭矩为1.1 kN。两者之间的偏差也很重要。根据解析计算，其差异等于力 F_SA = 1.8 kN。两者的区别只有有限元模型的一半，为 33.9 kN − 33 kN = 0.9 kN。

变形的情况下也有类似的偏差（见图09中的图）。显示的值为通过施加工作荷载折减的值。因此，变形必须通过工作荷载和预应力引起的变形来计算。示意图中的实际变形是u_z,1与平均变形之间的差值。分析参考值为f_SA 。变形 u_z,2为：

u_{z, 2} = u_{z, 1} - (\frac{0, 00385 0, 00381}{2} \frac{0, 00001 0, 00004}{2}) = 5, 5 μm - 3, 9 μm = 1, 6 μm < 3 μm = f_{SA}

公式 11

因此变形比计算的变形 f_Mmax小 1.4 μm。

最后，对结果杆中的结果进行比较。如图图 09 所示，结果杆件的荷载是受压，为 10.6 kN。该值必须与夹紧荷载 F_K = 10 kN 进行比较。由此得出 0.6 kN 的偏差。表 4 汇总了所有结果。

符号	解析值	有限元计算		偏差
符号	解析值	杆件	楼板	偏差
[F7]_Mmax [kN]	33,2	33,0	34,2	0.2/1.2
f_PMmax [μm]	5.0	-	5.6	0.6
f_SA [μm]	3.0	-	1.6	1.4
F_Mmax + F_SA [kN]	35,0	33,9	-	1.1
F_Mmax - F_PA [kN]	10.0	-	10,6	0.6

表 4 – 解析模型/有限元计算的比较值

评估

如表4所示，模型之间存在部分较大的差异。通常，最大的匹配出现在预应力荷载工况中。根据结果杆件（板）或螺栓杆件的评估，与 F_Mmax的偏差为 3.6% 或 0.6%（考虑分析结果）。

最大偏差是由施加工作荷载后的螺栓杆件和板的变形引起的。对杆件的轴力与解析值之间的偏差为1.1 kN。该偏差是关于解析解，初始值为 3%。但是在考虑螺栓附加力时，两者之间的差异会更大。有限元模型的偏差如下：
F_SA,FEM = (F_Mmax + F_SA ) - F_Mmax = 33,9 kN - 33 kN = 0,9 kN << 1,8 kN = F_SA

出现这种情况的原因是，两块板在 z 方向上都没有刚度，并且接触体在其厚度方向上只有一个有限元单元。因此在体内部不能有荷载扩展。实体荷载传递只能通过板的弯矩和剪力变形来实现。从数值可以明显看出，有限元模型中板和接触实体组合中预应力荷载工况下的刚度小于理论模型中的（变形较小的部分）。这里由梁的理论和螺栓所决定的截面可以排除螺栓刚度较大的那个。

另一方面，在有限元模型中的荷载组合的情况下，变形更小，或者螺栓力的增量明显更小。这再次表明板具有更高的刚度。总结起来，只有一种原因是：板和接触实体的组合具有不同的荷载延伸，因此公式 3.2 得出的在有限元模型中的方法不适用于该形式。因此，您可能需要通过举例和扩展的有限元模型来进行比较，以确定哪个更接近于实际情况。

但是，请注意以下几点：两种形式的残余夹紧力几乎相同。连接处的预应力可以很好地建模，并可用于节点分析。