Základy diagramu přípoje
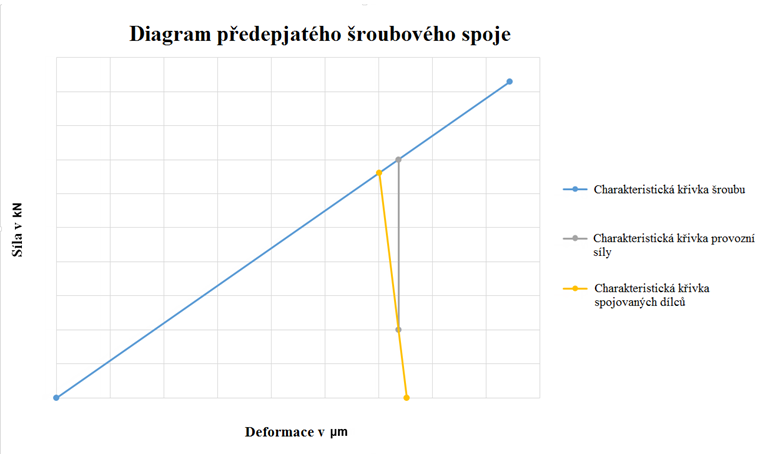
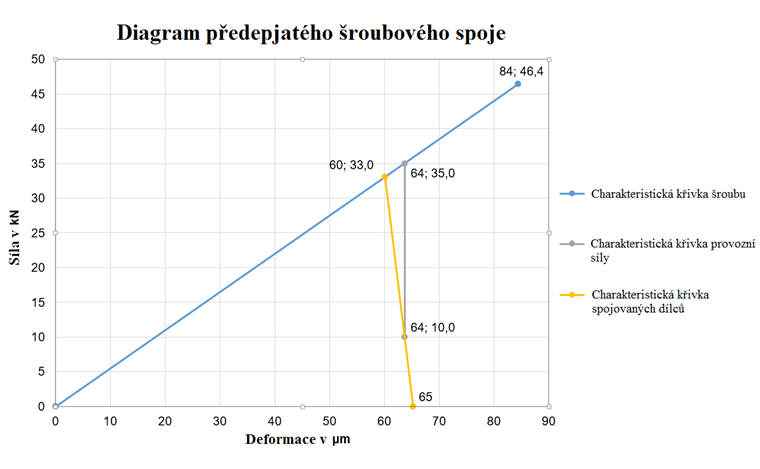
Diagram spoje představuje grafické znázornění sil v předpjatém šroubovém spoji. Tlakové síly vznikající ve spojovaných konstrukčních prvcích a s nimi spojené deformace se porovnávají se silami a deformacemi ve šroubu. Obrázek 01 ukazuje takový diagram.
Modrá linie (charakteristická linie) představuje graf šroubu, žlutá graf konstrukčních prvků. Obvykle je tuhost šroubů menší než tuhost konstrukčních prvků. Existují však také různé výjimky, jako například v případě matic. Průsečík obou linií představuje předpínací sílu ve spoji bez působícího vnějšího zatížení. Koncovým bodem linie šroubu je maximální odporová síla v závitu.
Kromě linie šroubu a dílčí linie je zde ještě jedna důležitá charakteristická linie vnější tahové síly (také předpětí). Tato linie je na Obrázku 01 znázorněna šedě. Vychází z charakteristické linie složek požadované zbytkové svěrné síly na ose y. Zbytková svěrná síla je síla, která ještě drží komponenty pohromadě. Pokud například kromě tahové složky u stávajícího provozního zatížení musí spoj přenášet také vodorovnou sílu (bez smykového protažení šroubu, tedy pouze třením složky), pak zbytková svěrná síla musí být zvolena tak, aby byla zajištěna dostatečná únosnost.
Kromě těchto charakteristických linií existují další linie, které lze použít pro podrobnější zobrazení. Protože však tyto linie nemají žádný vliv na základní postup, nebudeme je v tomto příspěvku dále vysvětlovat a použijeme pouze prezentované zjednodušené schéma spoje. Doplňkovými křivkami by například mohla být křivka udávající vliv sedání nebo excentrického napětí a zatížení.
Vzorce zjednodušeného diagramu spoje
Pro sestavení diagramu spoje je třeba nejdříve vypočítat příslušné tuhosti, deformace a síly. Obecně lze pružiny spočítat podle Hookova zákona následovně:
c = tuhost (konstanta tuhosti)
F = síla pružiny
f = deformace (vychýlení)
V případě taženého prutu z izotropního materiálu pak lze konstantu tuhosti stanovit přímo na základě modulu pružnosti:
E = modul pružnosti
A = průřezová plocha taženého prutu
l = délka taženého prutu
Pro stanovení tuhosti šroubu se zjednodušeně zohlední pouze dřík šroubu. Dále by bylo možné uvažovat hlavu šroubu, závit, matici, různé průměry dříku apod. Prvky v jejich převrácené hodnotě přitom přičítáme k celkové tuhosti. Tuhost pružiny šroubu (s dolním indexem S) vypočítáme pomocí následující rovnice:
cS = tuhost pružiny šroubu
ES = modul pružnosti šroubu
AS = průřezová plocha šroubu
lK = svěrná délka (výška/tloušťka dílců)
Pro průřezovou plochu v oblasti závitu šroubu se použije průměr boků profilu závitu d3. Celková rovnice má tak následující tvar:
Tuhost spojovaných dílců se vypočítá obdobně. Protože se zde jedná o jednu nebo o několik desek (ploch), použijeme index P:
cP = tuhost pružiny dílců/desek
EP = modul pružnosti desek
AP = průřezová plocha desek
lK = svěrná délka (výška/tloušťka dílců)
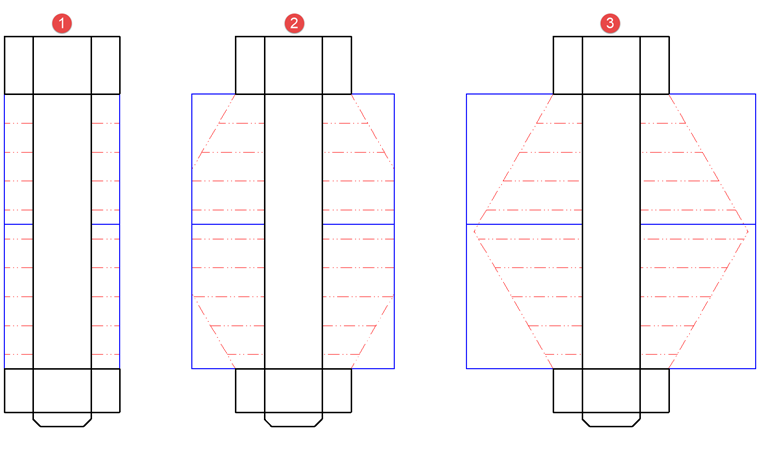
Průřezová plocha AP je na rozdíl od šroubu závislá na tloušťce. Vychází se z toho, že zatížení se roznáší pod úhlem asi 60°. Je přitom třeba rozlišovat tři případy, které vidíme na obr. 02.
V případě 1 představují spojované části mezi šroubem a maticí jakousi objímku, jejíž průměr je maximálně roven průměru dosedací plochy šroubu, případně matice.
Příklad 2 pokrývá oblast, kdy je průměr této objímky přinejmenším roven průměru dosedací plochy šroubu nebo matice a maximálně se rovná průměru kuželu roznášení zatížení (na obr. 02 červeně). Ta se táhne symetricky z obou stran a průměr je největší uprostřed upínací délky.
Případ 3 pokrývá oblast maximálního kužele roznášení zatížení až po nekonečné protažení desky. Z tohoto důvodu je třeba vypočítat náhradní plochu Aers. Aers pak odpovídá průřezové ploše náhradního válce s konstantním roznášením zatížení.
Pro následující analýzu postačuje v našem příkladu případ 3. Aers se přitom vypočítá pomocí níže uvedené rovnice (viz VDI 2230, rok vydání 1986 [1]):
dW = průměr dosedací plochy
dh = průměr otvoru
Průměr dosedací plochy můžeme přitom zjednodušeně uvažovat jako 90 % šířky klíče:
dW = 0,9 ∙ s (3.3)
s = šířka klíče na hlavu šroubu/matici
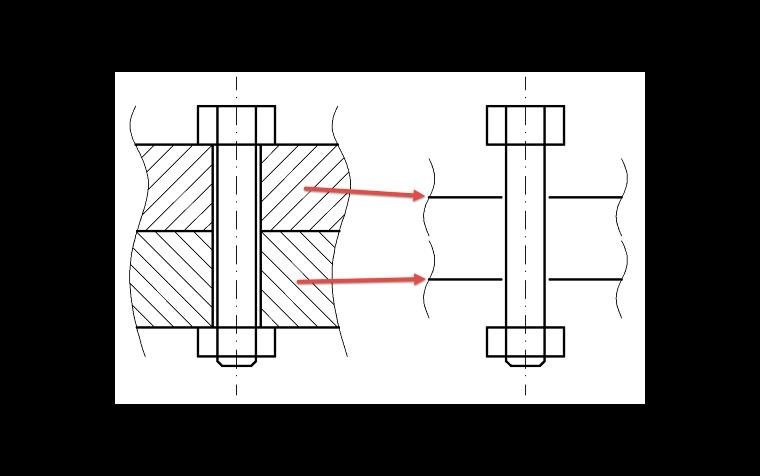
Vzhledem k tomu, že působiště zatížení u plošného modelu není nutně na horní straně dílce (desky), nýbrž vždy ve středové ploše, je třeba tuhost desky vypočítat v tomto místě působení zatížení. Pro daný účel se zavádí součinitel působení zatížení n, kterým se odpovídajícím způsobem redukuje svěrná délka. Daný problém je znázorněn na obr. 03.
Vlastní dílce, v našem případě dvě desky, se redukují na své středové plochy. V případě dvou desek je pak n vždy 0,5, protože se vždy použije polovina každé desky. Nová tuhost desek cPn se pak vypočítá následovně:
ΦK = poměr zatížení
Pro zakreslení charakteristických křivek potřebujeme kromě tuhostí ještě různé síly. Je třeba předem zadat zbytkovou svěrnou sílu FKR, provozní sílu FA a faktor utažení αA (postup utahování v závislosti na úhlu natočení). Výsledné minimální a maximální montážní síly FMmin a FMmax je oproti tomu třeba vypočítat. Níže uvádíme vzorec pro stanovení montážních sil, který zohledňuje postup utahování v závislosti na úhlu natočení:
FMmin = FKmin + FPA (3.6)
FMmax = αA ∙ FMmin (3.7)
αA = utahovací faktor pro způsob utahování podle úhlu natočení
FKmin = minimální nutná zbytková svěrná síla ve spoji
FPA = přídavná síla v desce od provozní síly
Přídavná síla v desce FPA je síla, která vzniká při působení provozní síly. Vypočítá se pomocí tohoto vzorce:
FPA = (1 - n ∙ ΦK) ∙ FA (3.8)
FA = provozní síla
Pokud budeme postupovat zjednodušeně a nebudeme uvažovat sedání, bude předpínací síla FV odpovídat minimální předpínací síle FMmin. Pro zohlednění charakteristické křivky provozní síly nám ještě chybí maximální síla ve šroubu FSmax, která vzniká ve šroubu při působení provozní síly:
FSmax = FMmax + FSA (3.9)
FSA = přídavná síla ve šroubu
Vzorec pro přídavnou sílu ve šroubu FSA je obdobou vzorce 3.8:
FSA = n∙ ΦK ∙ FA (3.10)
Jako poslední sílu nám zbývá stanovit maximální únosnost šroubu (F0,2), kterou určíme na základě průřezové plochy šroubu v oblasti závitu. Při jejím výpočtu se vychází z průměru průřezové plochy ds, který se stanoví ze střední hodnoty průměru jádra dk (d3) a průměru boků dfl (d2):
d2 = průměr boků závitu
d3 = průměr jádra závitu
fub = pevnost materiálu šroubu v tahu
Pro zakreslení charakteristických křivek do diagramu spoje je třeba kromě sil vypočítat odpovídající hodnoty deformací. Vzorec 1.1 proto upravíme pro výpočet f. Níže uvádíme rovnice pro stanovení deformací f k příslušným silám F:
Získáme tak následující body/hodnoty pro charakteristické křivky diagramu spoje:
| Křivka | Deformace | Síla |
|---|---|---|
| Šroub | 0 | 0 |
| f0,2 | F0,2 | |
| Plocha | fSMmax | FMmax |
| fSMmax + fPMmax nebo fMmax | 0 | |
| Provozní síla | fSMmax + fSA | FMmax - FPA |
| fSMmax + fSA | FMmax + FSA = FSmax |
Tabulka 1 - Body/hodnoty pro charakteristické křivky diagramu spoje
Modelování předpjatého šroubového spoje v programu RFEM
Model by měl být co možná přesný a zároveň proveditelný. Spoj tak budeme modelovat pomocí ploch, prutů a kontaktních těles.
Pro náš výpočetní příklad zadáme následující parametry:
FA = 25 kN
FK = 10 kN
ES = EP = 210 000 N/mm²
t1 = t2 = 10 mm
lK = t1 + t2 = 20 mm
dh = 10 mm
DA > dW + lK
n = 0,5
αA = 1,0
Šroub:
M10 8.8
fub = 800 N/mm²
d2 = 9,03 mm
d3 = 8,16 mm
s = 17 mm
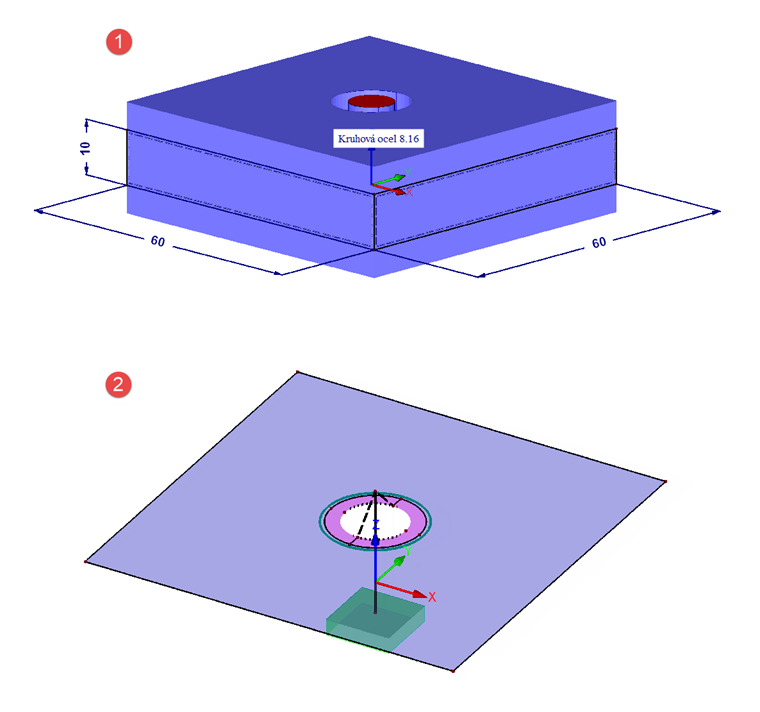
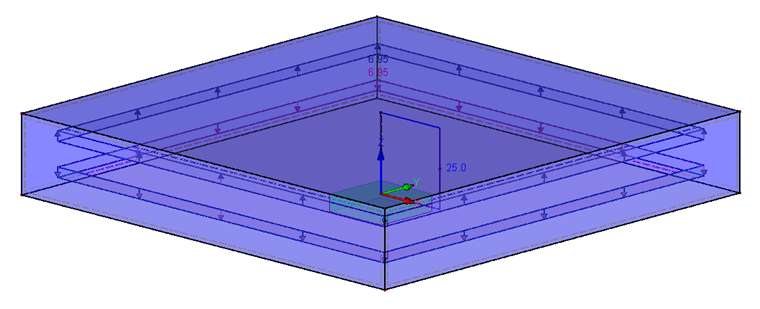
Model obsahuje dvě čtvercové plochy nad sebou, které mají uprostřed otvor o průměru dh a jejichž rozměry činí 60 x 60 mm (aby bylo splněno DA > dW + lK). Protože t1 = t2, je vzdálenost mezi deskami 10 mm. Zatížení působí přímo ve středu desky (neutrální vlákno). Z toho vyplývá, že n je 0,5. Model je podepřen na spodním konci prutu šroubu pevnou podporou. Má-li být podporová síla v součtu rovna nule, je třeba uvažovat zatížení jak na horní tak na spodní desce. Hodnota zatížení činí 6,95 N/mm² a odpovídá celkové síle 25 kN.
Pro dobrý přenos zatížení mezi šroubem (nosníkem) a deskami modelujeme okolo otvoru tuhou plochu (prstenec) s vnějším průměrem dW. Spojení mezi deskami se vytvoří pomocí tří kontaktních těles. Jedním z nich je těleso okolo otvoru vyjma části s tuhými plochami, dvě kontaktní tělesa leží jako dvě skořepiny okolo otvoru. Kontaktní tělesa musí být ze stejného materiálu jako desky, abychom správně zachytili tuhost mezi plochami. Kontakt je dále neúčinný při zdvihu a je u něj definováno tuhé tření ve vodorovném směru se součinitelem 0,1.
Konstrukce je znázorněna na obr. 04. Pod číslem 1 jsou zobrazeny plochy a pruty se svými skutečnými rozměry. Pod číslem 2 vidíme horní plochu s nosníkem (šroubem) a s tuhými pruty, které tvoří spojení mezi šroubem a deskou. Tuhá plocha (růžově) je přitom na vnitřní hraně také opatřena tuhým prutem, takže lze dobře přenášet jakékoli momenty.
Další důležitý bod představuje síť konečných prvků. Kvůli malým rozměrům jsme stanovili hlavní velikost sítě konečných prvků lFE na 2 mm. Navíc jsme zadali zahuštění sítě prvků lFE 0,2 mm na tuhých plochách.
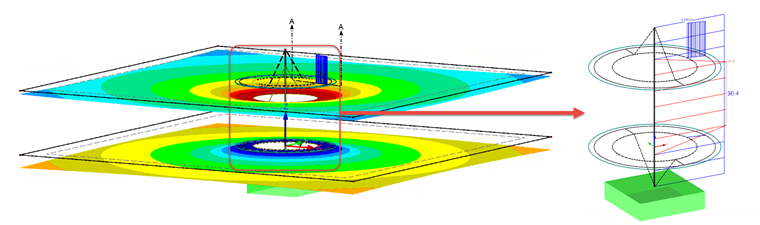
Vzhledem k tomu, že v praxi není znám ani průměr šroubu ani provozní síla na šroubu, nabízí se pro prvotní posouzení modelu a výpočet sil ve šroubu řešení bez otvoru a za použití tuhého prutu namísto nosníku. Toto modelové řešení pro předběžný návrh je znázorněno na obr. 05.
Abychom mohli zjistit zbytkové předpětí v modelu, zadali jsme rovnoběžně se šroubem (ve vzdálenosti 0,1 mm) výsledkový prut, který zahrnuje veškeré vnitřní síly kontaktního tělesa.
Porovnání analytického a numerického řešení
Pro porovnání řešení je třeba nejdříve vytvořit diagram předpjatého spoje. Hodnoty, které k tomu potřebujeme, jsou uvedeny v tabulce 1. Pokud za ně dosadíme hodnoty z našeho praktického příkladu (viz výše), dostaneme mezihodnoty a hodnoty pro charakteristické křivky diagramu, které vidíme v tabulce 2. Tabulka 3 předkládá souhrn nejdůležitějších hodnot podle tabulky 1 a na obr. 06 si můžeme prohlédnout sestavený diagram spoje.
| Bitmapa | Číslo vzorce | Hodnota |
|---|---|---|
| cS | 2.2 | 549 kN/mm |
| Aers | 3.2 | 303 mm² |
| cP | 3.1 | 3 182 kN/mm |
| ΦK | 3,5 | 0,147 |
| cPn | 3.4 | 6 921 kN/mm |
| FSA | 3.10 | 1,8 kN |
| fSA | 4.4 | 3 μm |
| FPA | 3.8 | 23,2 kN |
| FMmax | 3.6, 3.7 | 33,2 kN |
| fSMmax | 4.2 | 60 μm |
| fMmax | 4.3 | 65 μm |
| F0,2 | 3.11 | 46,2 kN |
| f0,2 | 4.1 | 84 μm |
Tabulka 2 - Mezihodnoty a výsledky výpočetního příkladu
| Křivka | Deformace [μm] | Síla [kN] |
|---|---|---|
| Šroub | 0 | 0,0 |
| 84 | 46,2 | |
| Plocha | 60 | 33,2 |
| 65 | 33,2 | |
| Provozní síla | 63 | 10,0 |
| 63 | 35,0 |
Tabulka 3 - Body/hodnoty pro charakteristické křivky diagramu výpočetního příkladu
V případě numerického řešení zadáme nejdříve dva zatěžovací stavy. První zatěžovací stav (ZS1 Předpětí) bude obsahovat zatížení na prut předpětím a druhý zatěžovací stav provozní zatížení (ZS2 Provozní zatížení). Dále se vytvoří kombinace zatížení z obou zatěžovacích stavů se součinitelem 1,0 (KZ1: ZS1 + ZS2). Výpočet se provede podle teorie prvního řádu s 15 zatěžovacími stupni (lepší konvergence u kontaktních těles se zadanou neúčinností).
Pro předpětí můžeme na prutu zadat zatížení typu počáteční předpětí nebo konečné předpětí. Vlastní předpínací síla je konečné předpětí. Protože výpočet zatížení typu konečné předpětí je časově náročný, doporučujeme zadat zatížení typu počáteční předpětí. Nevýhodou ovšem je, že zatížení v takovém případě nezohledňuje zpětnou sílu desek. Normálová síla v prutu je tak po skončení výpočtu příliš malá, protože je částečně snížena deformací desek. Tuto nesrovnalost lze odstranit dvěma způsoby. Zaprvé lze vzniklý rozdíl odhadnout z deformace desek a přepočítat ho na (předpokládanou) přídavnou sílu FZus,v pomocí následujícího vzorce:
FZus,v = fPMmax ∙ cS (5.1)
Zadruhé lze daný rozdíl stanovit iteračním výpočtem. K tomu je třeba vypočítat zatěžovací stav předpětí. Rozdíl mezi uvažovaným počátečním předpětím a výslednou normálovou silou pak odpovídá přídavné síle FZus,i (iteračně stanovené). Použít lze přitom následující rovnici:
FZus,i = FMmax - NS (5.2)
NS = normálová síla v prutu při počátečním předpětí FMmax
Přídavná síla FZus,v se stanoví na základě hodnot z tabulky 2 následovně:
FZus,v = fPMmax ∙ cS = (fMmax - fSMmax) ∙ cS = 5 μm ∙ 549 kN/mm = 2,8 kN
Iteračně stanovenou přídavnou sílu FZus,i můžeme po výpočtu zatěžovacího stavu na prutu vyčíst z obr. 07.
FZus,i = 33,2 kN - 30,4 kN = 2,8 kN
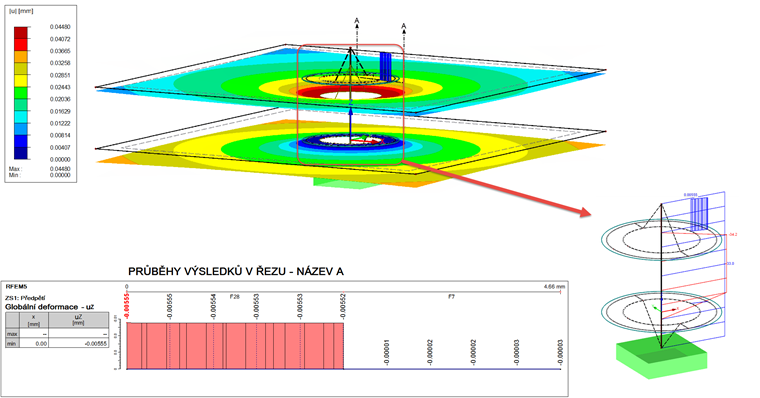
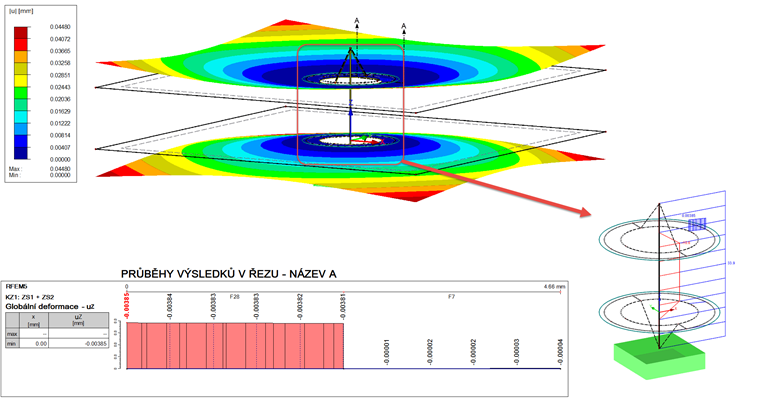
Předpětí tak v obou případech činí 36 kN. Zatěžovací stav lze nyní znovu přepočítat. Výsledek vidíme na obr. 08.
Přídavný výsledkový prut, který integruje kontaktní síly všech kontaktních těles, dosahuje výsledku 34,2 kN. To je o 1,2 kN více, než normálová síla na prutu šroubu, která činí 33 kN. Pro porovnání s fPMmax je třeba přičíst deformaci obou ploch (F1 a F27), která je znázorněna v diagramu. V průměru dostaneme tento výsledek:
Deformace je tak o 0,6 μm větší než vypočítaná deformace fMmax.
Výsledek výpočtů za působení provozní síly v KZ1 je znázorněn na obr. 09.
Výsledná síla na prutu šroubu je 33,9 kN. Tuto sílu na prutu lze porovnat se silou FSmax = 35 kN (viz tabulka 1 a 3, provozní síla). Odchylka činí 1,1 kN. Odchylka v rozdílech je tu také důležitá. Podle analytického výpočtu by měl rozdíl odpovídat síle FSA = 1,8 kN. Model konečných prvků ovšem vykazuje hodnotou 33,9 kN - 33 kN = 0,9 kN pouze poloviční rozdíl.
K obdobně velkým odchylkám dospějeme v případě deformace (viz diagram na obr. 09). V případě zde zobrazené hodnoty se jedná o hodnotu, která je redukovaná provozní silou. Následně je tak třeba stanovit deformaci vyvolanou působením provozní síly na základě deformace předpětím. Vlastní deformace pak odpovídá rozdílu uz,1 a průměrné hodnoty deformace v diagramu. Analytická hodnota pro porovnání je fSA. Pro deformaci uz,2 tak platí:
Deformace je tak o 1,4 μm menší než vypočítaná deformace fMmax.
Nakonec ještě porovnáme výsledky na výsledkovém prutu. Při zatížení dostaneme podle obr. 09 pro výsledkový prut tlakovou sílu 10,6 kN. Tuto hodnotu je třeba porovnat se svěrnou silou FK = 10 kN, z čehož vyplývá odchylka 0,6 kN. V tabulce 4 znovu shrneme veškeré výsledky.
| Bitmapa | Analytická Hodnota | Výpočet MKP | Odchylka | |
|---|---|---|---|---|
| Prut | Plocha | |||
| FMmax [kN] | 33,2 | 33,0 | 34,2 | 0,2 / 1,2 |
| fPMmax [μm] | 5,0 | - | 5,6 | 0,6 |
| fSA [μm] | 3,0 | - | 1,6 | 1,4 |
| FMmax + FSA [kN] | 35,0 | 33,9 | - | 1,1 |
| FMmax - FPA [kN] | 10,0 | - | 10,6 | 0,6 |
Tabulka 4 - Hodnoty pro porovnání analytického modelu /výpočtu MKP
Vyhodnocení
Jak je zřejmé z tabulky 4, zčásti jsme mezi oběma modely zaznamenali velké rozdíly. Největší shodu lze obecně pozorovat v zatěžovacím stavu předpětí. Odchylky ve FMmax činí v případě vyhodnocení výsledkového prutu (desky) 3,6 % a při vyhodnocení prutu šroubu 0,6 % (vztaženo k výsledku analytického výpočtu).
Největší odchylku vykazuje výsledek u prutu šroubu a deformace desek po zohlednění provozní síly. V tomto případě se normálová síla na prutu odchyluje od analytického řešení o 1,1 kN. Tato odchylka činí ve vztahu k analytickému řešení zprvu 3 %. Ovšem vzhledem k přídavné síle ve šroubu je rozdíl podstatně větší. Odchylka pro model MKP se stanoví následovně:
FSA,FEM = (FMmax + FSA) - FMmax = 33,9 kN - 33 kN = 0,9 kN << 1,8 kN = FSA
Příčinou těchto odchylek může být to, že obě desky nemají žádnou tuhost ve směru z a kontaktní těleso má při své tloušťce pouze jeden konečný prvek. Zatížení se tak nemůže po tělese roznášet. Další přenos zatížení v tělese probíhá výlučně formou deformace desky ohybem a posouvající silou. Pokud se na hodnoty pozorně podíváme, zjistíme, že model KP v zatěžovacím stavu předpětí ve spojení desek a kontaktního tělesa vykazuje menší tuhost než analytický model (viz menší deformace). Na tomto místě lze vyloučit větší tuhost šroubu, neboť tato tuhost je pevně dána průřezem a teorií nosníků.
Na druhé straně jsme v případě kombinace zatížení v modelu MKP zaznamenali menší deformaci, respektive síla ve šroubu vykazuje podstatně menší růst. To ukazuje opět na větší tuhost v desce. Společně se tak nabízí jediné vysvětlení: spojení desky a kontaktního tělesa vykazuje jiné roznášení zatížení, a tak použití vzorce 3.2 v modelu MKP není v daném tvaru platné. Pravděpodobně by tu bylo třeba na reálném příkladu nebo na rozšířeném modelu MKP prověřit, které z obou řešení více odpovídá skutečnosti.
Čeho je ovšem třeba si všimnout, je téměř totožná zbytková svěrná síla v obou případech. Předpětí ve spoji je tudíž modelováno dobře a lze ho použít pro posouzení spojů.
Závěr
Modelování předepjatého šroubového spoje pomocí kontaktních těles, ploch a nosníků představuje kompromis mezi praktickým řešením a reálným ztvárněním. Praktičností jsou tu myšleny podstatně nižší časové nároky na výpočet v porovnání s výpočtem prostorového modelu MKP, od něhož lze zas ovšem očekávat větší přesnost. Posouzení šroubu nicméně není bez výhrad nebo případně je tu třeba provést další analýzu, která výsledky přiblíží realitě.
Protože se však předpínací síly i zbytkové svěrné síly do značné míry shodují s výsledky analytického výpočtu, lze tento způsob modelování považovat za zcela vhodný postup pro posouzení spojů.