Grundlagen Verspannungsdreieck
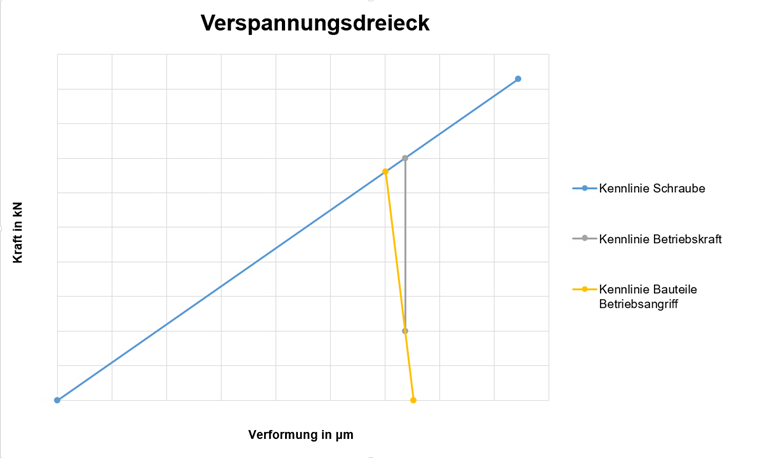
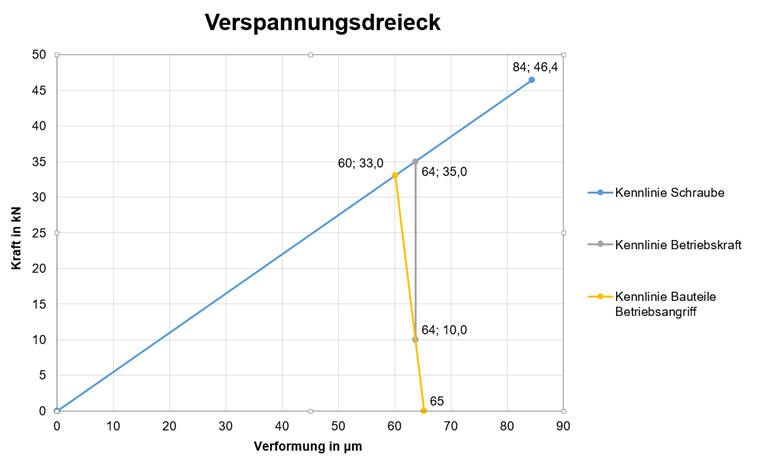
Das Verspannungsdreieck dient der grafischen Darstellung der Kräfte in einer vorgespannten Schraubverbindung. Dabei werden die in den zu verbindenden Bauteilen entstehenden Druckkräfte und damit einhergehenden Verformungen den Kräften und Verformungen in der Schraube gegenübergestellt. In Bild 01 ist ein solches Dreieck dargestellt.
Die blaue Linie (Kennlinie) stellt den Graphen für die Schraube dar, die gelbe den für die Bauteile. Typischerweise ist die Steifigkeit der Schraube kleiner als die der Bauteile. Es gibt aber auch diverse Ausnahmen wie zum Beispiel bei Hülsen. Der Schnittpunkt der beiden Linien gibt die Vorspannkraft in der Verbindung ohne äußere Belastung wieder. Der Endpunkt der Schraubenkennlinie ist die maximal aufnehmbare Kraft im Gewinde.
Neben der Schraubenkennlinie und der Kennlinie der Bauteile gibt es noch eine weitere wichtige Kennlinie, nämlich die der äußeren Zugkrafteinwirkung (auch Betriebskraft). Diese Kennlinie wird im Bild grau dargestellt. Ihr Ursprung liegt auf der Kennlinie der Bauteile an der y-Stelle der gewünschten Restklemmkraft. Dabei ist die Restklemmkraft die Kraft, welche die Bauteile noch zusammenhält. Wenn zum Beispiel bei einer vorhandenen Betriebskraft neben dem Zuganteil auch noch eine horizontale Kraft von der Verbindung aufgenommen werden soll (ohne Scherung der Schraube, also nur durch Reibung der Bauteile), dann muss die Restklemmkraft so gewählt werden, dass auch hier eine ausreichende Sicherheit vorliegt.
Es gibt neben diesen Kennlinien noch weitere, welche für eine detailliertere Abbildung verwendet werden können. Da diese aber auf die prinzipielle Vorgehensweise keinen Einfluss haben, wird hier nicht weiter auf sie eingegangen und das vorgestellte vereinfachte Verspannungsdreieck verwendet. Zusätzliche Kennlinien wären zum Beispiel die aus Setzung oder exzentrischer Verspannung und Belastung.
Formeln des vereinfachten Verspannungsdreiecks
Für das Aufstellen des Verspannungsdreiecks müssen zuerst die zugehörigen Steifigkeiten, Verformungen und Kräfte berechnet werden. Im Allgemeinen lassen sich Federsteifigkeiten nach dem hookeschen Gesetz wie folgt berechnen:
c = Steifigkeit (Federkonstante)
F = Federkraft
f = Verformung (Auslenkung)
Bei einem Zugstab mit isotropem Material lässt sich dann die Federkonstante auch direkt über das Elastizitätsmodul (E-Modul) berechnen:
E = Elastizitätsmodul
A = Querschnittsfläche des Zugstabs
l = Länge des Zugstabs
Für die Steifigkeit der Schraube wird vereinfacht nur der Schraubenschaft angesetzt. Weitere Möglichkeiten sind der Ansatz von Schraubenkopf, Gewinde, Mutter, verschiedene Schaftdurchmesser et cetera. Dabei werden die Elemente mit ihrem Kehrwert zur Gesamtsteifigkeit addiert. Die Federsteifigkeit der Schraube errechnet sich mit folgender Formel (Index S):
cS = Federsteifigkeit der Schraube
ES = E-Modul der Schraube
AS = Querschnittsfläche der Schraube
lK = Klemmlänge (Höhe/Dicke der Bauteile)
Für die Querschnittsfläche im Bereich des Gewindes der Schraube wird der Gewindeflankendurchmesser d3 verwendet. Damit ergibt sich als Gesamtformel:
Die Steifigkeit der Bauteile wird ähnlich berechnet. Da es sich hier um eine oder mehrere Platten handelt, wird der Index P verwendet:
cP = Federsteifigkeit der Bauteile/Platten
EP = E-Modul der Platten
AP = Querschnittsfläche der Platten
lK = Klemmlänge (Höhe/Dicke der Bauteile)
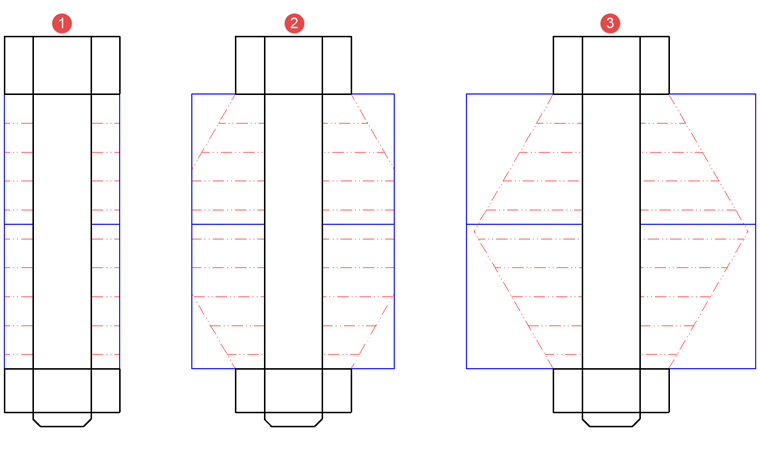
Die Querschnittsfläche AP ist im Gegensatz zur Schraube dickenabhängig. Es wird davon ausgegangen, dass sich die Last unter einem Winkel von zirka 60° ausbreitet. Dabei gibt es drei Fälle zu unterscheiden, welche in Bild 02 dargestellt werden.
Bei Fall 1 sind die Bauteile zwischen Schraube und Mutter wie eine Hülse und der Durchmesser dieser Hülse ist maximal gleich dem Durchmesser der Auflagefläche von Schraube beziehungsweise Mutter.
Fall 2 deckt den Bereich ab, bei dem der Durchmesser dieser Hülse minimal gleich dem Durchmesser der Auflagefläche von Mutter oder Schraube ist und maximal gleich dem Durchmesser des Lastausbreitungskegels (in Bild 02 rot). Dieser erstreckt sich von beiden Seiten symmetrisch und in der Mitte der Klemmlänge ist der Durchmesser am größten.
Fall 3 deckt den Bereich vom maximalen Lastausbreitungskegel bis hin zur unendlichen Plattenausdehnung ab. Aus diesem Grund muss eine Ersatzfläche Aers berechnet werden. Aers entspricht dann der Querschnittsfläche eines Ersatzzylinders mit konstanter Lastausbreitung.
Für die folgenden Betrachtungen genügt Fall 3. Aers berechnet sich dabei mit folgender Formel (siehe VDI 2230, Ausgabe 1986 [1]):
dW = Durchmesser Auflagefläche
dh = Durchmesser Bohrung
Der Durchmesser der Auflagefläche kann dabei vereinfacht mit 90 % der Schlüsselweite angenommen werden:
dW = 0,9 ∙ s (3.3)
s = Schlüsselweite des Schraubenkopfes/der Mutter
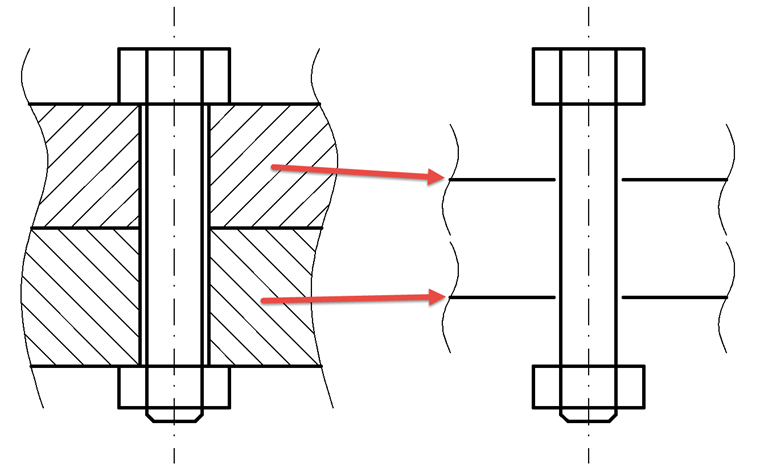
Da der Lastangriffspunkt bei einem Flächenmodell zwangläufig nicht an der Oberseite des Bauteils (der Platte) erfolgt, sondern stets in der Mittelfläche, muss die Plattensteifigkeit an diesem Lastangriffspunkt ermittelt werden. Dafür wird der Lastangriffsfaktor n eingeführt, welcher die Klemmlänge entsprechend abmindert. Eine Veranschaulichung dieser Problematik zeigt Bild 03.
Die eigentlichen Bauteile, in diesem Fall zwei Platten, werden auf ihre Mittelflächen reduziert. Im Falle von zwei Platten ist n dann immer 0,5, da stets die Hälfte jeder Platte verwendet wird. Die neue Plattensteifigkeit cPn errechnet sich dann wie folgt:
ΦK = Lastverhältnis
Für das Aufstellen der Kennlinien werden neben den Steifigkeiten auch noch diverse Kräfte benötigt. Die Restklemmkraft FKR, die Betriebskraft FA, und der Anziehfaktor αA (drehwinkelgesteuertes Anziehverfahren) müssen vorgegeben werden. Die resultierenden minimalen und maximalen Montagekräfte FMmin und FMmax hingegen müssen errechnet werden. Nachstehend die Formel für die Montagekräfte bei der Verwendung eines drehwinkelgesteuerten Anziehverfahrens:
FMmin = FKmin + FPA (3.6)
FMmax = αA ∙ FMmin (3.7)
αA = Anziehfaktor drehwinkelgesteuertes Verfahren
FKmin = minimal erforderliche Restklemmkraft in der Verbindung
FPA = Plattenzusatzkraft durch Betriebskraft
Die Plattenzusatzkraft FPA ist die Kraft, welche bei Anliegen der Betriebskraft erzeugt wird. Sie berechnet sich nach der Formel:
FPA = (1 - n ∙ ΦK) ∙ FA (3.8)
FA = Betriebskraft
Die Vorspannkraft FV entspricht bei der Vereinfachung ohne Betrachtung von Setzungen der minimalen Vorspannkraft FMmin. Für die Betrachtung der Kennlinie der Betriebskraft fehlt noch die maximale Schraubenkraft FSmax, welche bei Anliegen der Betriebskraft in der Schraube entsteht:
FSmax = FMmax + FSA (3.9)
FSA = Schraubenzusatzkraft
Die Schraubenzusatzkraft FSA wiederum errechnet sich analog zu Formel 3.8:
FSA = n∙ ΦK ∙ FA (3.10)
Die maximale Tragkraft der Schraube (F0,2) als letzte noch fehlende Kraft muss über den Spannungsquerschnitt ermittelt werden. Dieser errechnet sich mit Hilfe des Spannungsdurchmessers ds, der sich aus dem Mittelwert von Kerndurchmesser dk (d3) und dem Flankendurchmesser dfl (d2) ergibt:
d2 = Flankendurchmesser des Gewindes
d3 = Kerndurchmesser des Gewindes
fub = Zugfestigkeit des Schraubenmaterials
Neben den Kräften müssen die Verformungen als korrespondierende Werte ermittelt werden, damit die Kennlinien im Verspannungsdreieck eingetragen werden können. Dazu dient die nach f umgestellte Formel 1.1. Nachstehend die Formeln für die Verformungen f zu den jeweiligen Kräften F:
Damit ergeben sich folgende Kennlinienpunkte/-werte für das Verspannungsdreieck:
| Kennlinie | Verformung | Kraft |
|---|---|---|
| Schraube | 0 | 0 |
| f0,2 | F0,2 | |
| Platte | fSMmax | FMmax |
| fSMmax + fPMmax oder fMmax | 0 | |
| Betriebskraft | fSMmax + fSA | FMmax - FPA |
| fSMmax + fSA | FMmax + FSA = FSmax |
Tabelle 1 - Kennlinienpunkte/-werte für das Verspannungsdreieck
Modellierung einer vorgespannten Schraubenverbindung in RFEM
Das Modell soll eine gute Mischung aus Genauigkeit und Praktikabilität bilden. Daher wird die Verbindung mit Hilfe von Flächen, Stäben und Kontaktvolumen erfolgen.
Für ein Rechenbeispiel werden daher folgende Parameter vorgegeben:
FA = 25 kN
FK = 10 kN
ES = EP = 210.000 N/mm²
t1 = t2 = 10 mm
lK = t1 + t2 = 20 mm
dh = 10 mm
DA > dW + lK
n = 0,5
αA = 1,0
Schraube:
M10 8.8
fub = 800 N/mm²
d2 = 9,03 mm
d3 = 8,16 mm
s = 17 mm
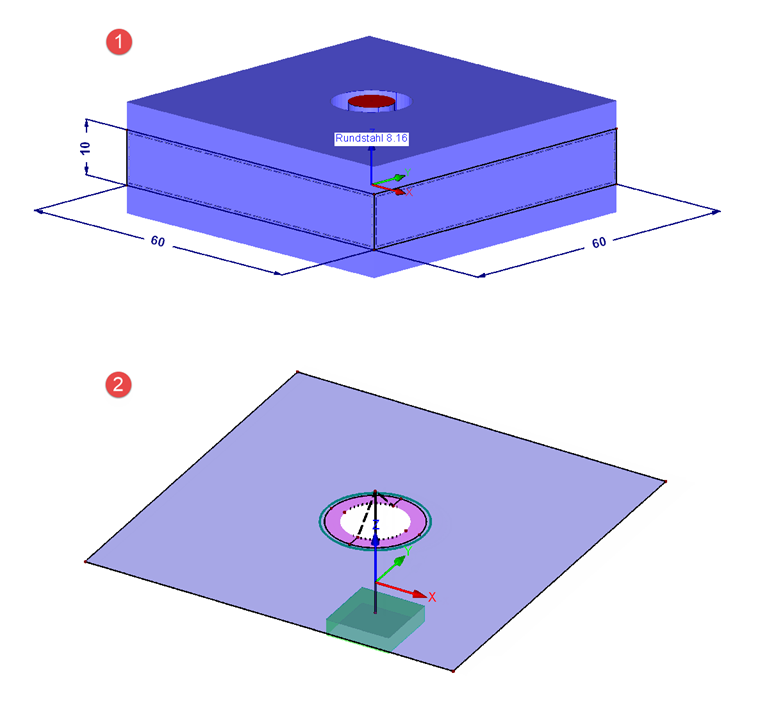
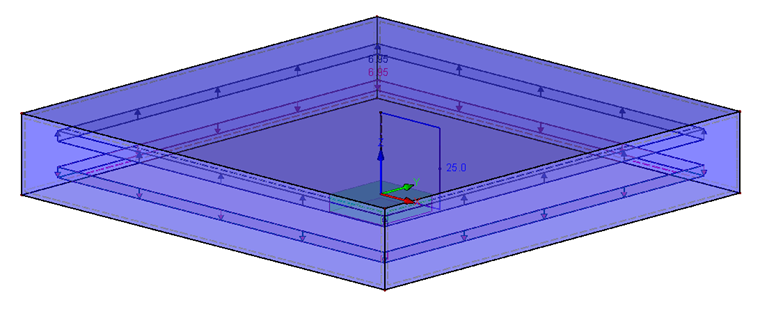
Das Modell beinhaltet zwei übereinanderliegende quadratische Flächen mit einem Loch (Durchmesser dh) in der Mitte, welche die Abmessungen 60 x 60 mm haben (um DA > dW + lK zu erfüllen). Da t1 = t2, ergibt sich ein Plattenabstand von 10 mm. Die Last greift direkt in Plattenmitte an (neutrale Faser). Dadurch ist n mit 0,5 angegeben. Die Lagerung des Modells erfolgt am unteren Ende des Schraubenstabes mit einem Festlager. Damit die Lagerkraft in Summe null ergibt, muss dann die Last sowohl an der oberen als auch unteren Platte angebracht werden. Die Last ergibt sich zu 6,95 N/mm² für 25 kN Gesamtkraft.
Für einen guten Lastübertrag zwischen Schraube (Balkenstab) und Platten wird um das Loch eine starre Fläche (Ring) mit dem äußeren Durchmesser dW modelliert. Die Verbindung zwischen den Platten wird über drei Kontaktvolumen erzeugt. Eines ist das Volumen um das Loch ohne den Teil mit den starren Flächen, zwei Kontaktvolumen liegen wie zwei Schalen um das Loch. Die Kontaktvolumina müssen das gleiche Material wie die Platten haben, um die Steifigkeit zwischen den Platten korrekt wiedergeben zu können. Zusätzlich fällt der Kontakt beim Abheben aus und hat eine starre Reibung in horizontaler Richtung mit dem Faktor 0,1.
Die Struktur ist in Bild 04 dargestellt. Unter Nummer 1 werden die Flächen und Stäbe mit ihren tatsächlichen Abmessungen dargestellt. Nummer 2 zeigt die obere Fläche mit Balkenstab (Schraube) und den Starrstäben, welche die Verbindung zwischen Schraube und Platte herstellen. Die starre Fläche (pink) wird dabei an der Innenkante ebenfalls mit einem Starrstab versehen, sodass jegliche Momente gut übertragen werden können.
Ein weiterer wichtiger Punkt ist das FE-Netz. Wegen der geringen Abmessungen wurde als Haupt-FE-Netzgröße für lFE 2 mm festgelegt. Zudem wurden Flächennetzverdichtungen mit lFE 0,2 mm an den Starrflächen definiert.
Da in der Praxis weder Schraubendurchmesser noch Betriebskraft an der Schraube bekannt sind, bietet sich für die erste Betrachtung des Modells und die Ermittlung der Schraubenkräfte die Modellierung ohne Bohrung und statt eines Balkenstabs die Verwendung eines Starrstabes an. Diese Modellierung für die Vordimensionierung ist in Bild 05 dargestellt.
Um die Restvorspannung im Modell ablesen zu können, wurde ein Ergebnisstab parallel zur Schraube (Abstand 0,1 mm) angesetzt. Dieser integriert alle Schnittgrößen des Kontaktvolumens auf.
Vergleich von analytischer und numerischer Lösung
Für den Vergleich muss zunächst das Verspannungsdreieck aufgestellt werden. Die dafür benötigten Werte sind in Tabelle 1 aufgelistet. Durch das Einsetzen der Werte für das praktische Beispiel (siehe oben) erhält man die in Tabelle 2 dargestellten Zwischenwerte und Kennlinienwerte. Tabelle 3 enthält zusammengefasst die wichtigsten Werte analog zu Tabelle 1 und Bild 06 zeigt das fertige Verspannungsdreieck.
| Formelzeichen | Formelnummer | Wert |
|---|---|---|
| cS | 2.2 | 549 kN/mm |
| Aers | 3.2 | 303 mm² |
| cP | 3.1 | 3.182 kN/mm |
| ΦK | 3.5 | 0,147 |
| cPn | 3.4 | 6.921 kN/mm |
| FSA | 3.10 | 1,8 kN |
| fSA | 4.4 | 3 μm |
| FPA | 3.8 | 23,2 kN |
| FMmax | 3.6, 3.7 | 33,2 kN |
| fSMmax | 4.2 | 60 μm |
| fMmax | 4.3 | 65 μm |
| F0,2 | 3.11 | 46,2 kN |
| f0,2 | 4.1 | 84 μm |
Tabelle 2 - Zwischenergebnisse und Ergebnisse des Rechenbeispiels
| Kennlinie | Verformung [μm] | Kraft [kN] |
|---|---|---|
| Schraube | 0 | 0,0 |
| 84 | 46,2 | |
| Platte | 60 | 33,2 |
| 65 | 33,2 | |
| Betriebskraft | 63 | 10,0 |
| 63 | 35,0 |
Tabelle 3 - Kennlinienpunkte/-werte des Rechenbeispiels
Für die numerische Lösung wurden zunächst zwei Lastfälle angelegt. Der erste Lastfall (LF1 Vorspannung) beinhaltet die Stablast der Vorspannung und der zweite (LF2 Betriebslast) die Betriebslast. Zusätzlich wurde eine Lastkombination aus beiden Lastfällen (Faktor 1,0) erzeugt (LK1: LF1 + LF2). Die Berechnung erfolgt nach Theorie erster Ordnung mit 15 Laststufen (bessere Konvergenz bei Kontaktvolumen mit Ausfall).
Für die Vorspannung kann am Stab die Stablast Anfangsvorspannung oder Endvorspannung verwendet werden. Die eigentliche Vorspannkraft ist eine Endvorspannung. Da die Last Endvorspannung einen hohen Rechenaufwand benötigt, ist es ratsam, die Stablast Anfangsvorspannung zu verwenden. Diese hat aber den Nachteil, dass die so aufgebrachte Last nicht die rückstellende Kraft durch die Platten beinhaltet. Damit ist nach dem Fertigstellen der Berechnung die Normalkraft im Stab zu gering, da ein Teil durch Verformung der Platten abgebaut werden kann. Diese Differenz kann auf zwei Wegen abgebaut werden. Zum einen kann diese über die Verformung der Platten vorausgesagt und in eine Zusatzkraft FZus,v (vorausgesagt) umgerechnet werden nach folgender Formel:
FZus,v = fPMmax ∙ cS (5.1)
Alternativ kann diese auch iterativ bestimmt werden. Dazu muss der Vorspannungslastfall berechnet werden. Die Differenz zwischen aufgebrachter Anfangsvorspannung und der resultierenden Normalkraft im Stab entspricht dann der Zusatzkraft FZus,i (iterativ). Nachfolgende Formel kann dazu verwendet werden:
FZus,i = FMmax - NS (5.2)
NS = Normalkraft im Stab bei Anfangsvorspannung FMmax
Die Zusatzkraft FZus,v ergibt sich nach den Werten aus Tabelle 2 wie folgt:
FZus,v = fPMmax ∙ cS = (fMmax - fSMmax) ∙ cS = 5 μm ∙ 549 kN/mm = 2,8 kN
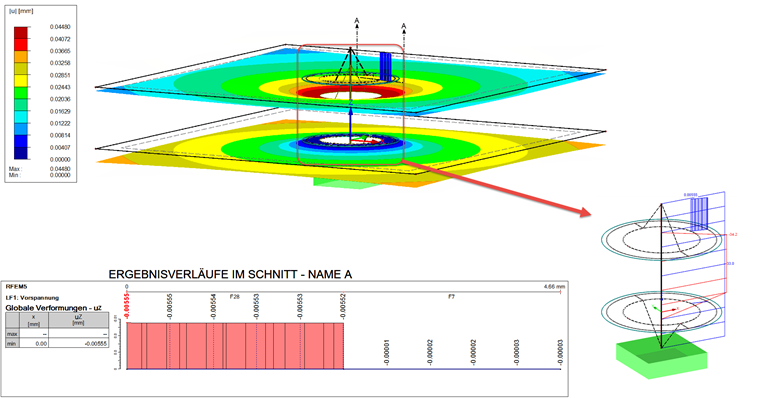
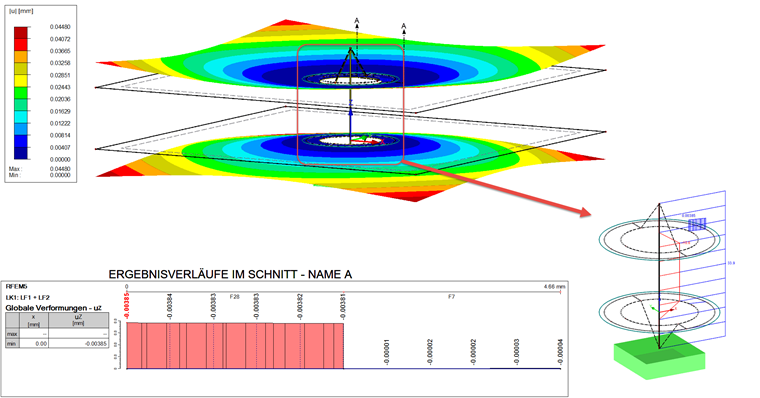
Die iterative Zusatzkraft FZus,i kann nach Berechnung des Lastfalls am Stab in Bild 07 abgelesen werden.
FZus,i = 33,2 kN - 30,4 kN = 2,8 kN
Die Vorspannung ergibt sich also in beiden Fällen zu 36 kN. Damit lässt sich der Lastfall neu berechnen. Das Resultat ist in Bild 08 dargestellt.
Der zusätzliche Ergebnisstab, welcher die Kontaktkräfte aller Kontaktvolumen aufaddiert, hat als Ergebnis 34,2 kN. Dies liegt um 1,2 kN über der Normalkraft des Schraubenstabes mit 33 kN. Die im Diagramm dargestellte Verformung von beiden Flächen (F1 und F27) muss addiert werden, um sie mit fPMmax vergleichen zu können. Im Mittel ergibt sich diese wie folgt:
Die Verformung ist damit um 0,6 μm größer als die errechnete Verformung fMmax.
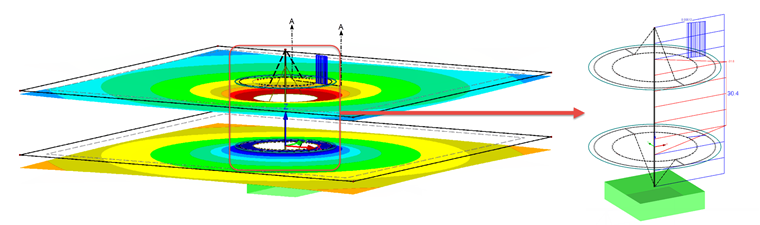
Ein Resultat der Berechnungen unter der Betriebslast in LK1 ist in Bild 09 dargestellt.
Der Schraubenstab hat als Ergebnis 33,9 kN. Diese Stabkraft kann der Kraft FSmax = 35 kN gegenübergestellt werden (siehe Tabellen 1 und 3, Betriebskraft). Die Abweichung beträgt 1,1 kN. Die Abweichung der Differenzen ist hier auch von Bedeutung. Nach der analytischen Berechnung sollte die Differenz gleich der Kraft FSA = 1,8 kN sein. Die Differenz des FE-Modells ist allerdings mit 33,9 kN - 33 kN = 0,9 kN lediglich halb so groß.
Ähnlich große Abweichungen erhält man bei der Verformung (siehe Diagramm in Bild 09). Der hier dargestellte Wert ist der durch die Betriebskraft verminderte Wert. Folglich muss die Verformung durch die Betriebskraft mit Hilfe der Verformung durch die Vorspannung errechnet werden. Die eigentliche Verformung ist dann die Differenz aus uz,1 und der mittleren Verformung im Diagramm. Der analytische Vergleichswert ist fSA. Damit ergibt sich für die Verformung uz,2:
Die Verformung ist damit um 1,4 μm kleiner als die errechnete Verformung fMmax.
Zuletzt noch der Vergleich der Ergebnisse im Ergebnisstab. Unter Belastung ergibt sich laut Bild 09 für den Ergebnisstab eine Druckkraft von 10,6 kN. Dieser Wert muss mit der Klemmkraft FK = 10 kN verglichen werden. Hier ergibt sich eine Abweichung von 0,6 kN. Tabelle 4 fasst nochmal alle Ergebnisse zusammen.
| Formelzeichen | Analytischer Wert | FEM-Rechnung | Abweichung | |
|---|---|---|---|---|
| Stab | Platte | |||
| FMmax [kN] | 33,2 | 33,0 | 34,2 | 0,2 / 1,2 |
| fPMmax [μm] | 5,0 | - | 5,6 | 0,6 |
| fSA [μm] | 3,0 | - | 1,6 | 1,4 |
| FMmax + FSA [kN] | 35,0 | 33,9 | - | 1,1 |
| FMmax - FPA [kN] | 10,0 | - | 10,6 | 0,6 |
Tabelle 4 - Vergleichswerte analytisches Modell/FEM-Rechnung
Auswertung
Wie in Tabelle 4 ersichtlich, gibt es teilweise große Differenzen zwischen den Modellen. Die größten Übereinstimmungen liegen, allgemeiner betrachtet, im Lastfall Vorspannung. Die Abweichungen von FMmax liegen je nach Betrachtung des Ergebnisstabes (Platte) oder des Schraubenstabes bei 3,6 % beziehungsweise 0,6 % (bezogen auf das analytische Ergebnis).
Die größte Abweichung liegt im Ergebnis des Schraubenstabes und der Plattenverformung nach dem Aufbringen der Betriebskraft. Hier besteht zwischen der Normalkraft am Stab und der analytischen Lösung eine Abweichung von 1,1 kN. Diese Abweichung beträgt, bezogen auf die analytische Lösung, zunächst 3 %. Aber in Bezug auf die Schraubenzusatzkraft ist der Unterschied wesentlich größer. Die Abweichung ergibt sich für das FEM-Modell wie folgt:
FSA,FEM = (FMmax + FSA) - FMmax = 33,9 kN - 33 kN = 0,9 kN << 1,8 kN = FSA
Diese Abweichungen können dadurch zustande kommen, dass die beiden Platten keine Steifigkeit in z-Richtung haben und das Kontaktvolumen lediglich ein FE-Element in seiner Dicke besitzt. Demzufolge kann es zu keiner Lastausbreitung innerhalb des Volumens kommen. Die Lastweiterleitung im Volumen erfolgt ausschließlich über die Verformung der Platte durch Biegung und Querkraft. Wenn man die Werte betrachtet, dann wird ersichtlich, dass im FE-Modell im Lastfall Vorspannung im Verbund von Platten und Kontaktvolumen eine geringere Steifigkeit vorliegt als im analytischen Modell (siehe geringere Verformung). Es kann an dieser Stelle eine höhere Steifigkeit der Schraube ausgeschlossen werden, da diese durch die Balkentheorie und den Querschnitt feststeht.
Auf der anderen Seite wird bei der Lastkombination im FEM-Modell eine geringere Verformung ausgegeben beziehungsweise die Schraubenkraft hat einen wesentlich geringeren Zuwachs. Das wiederum deutet auf eine höhere Steifigkeit in der Platte hin. Zusammen betrachtet gibt es dafür nur eine Erklärung: Der Verbund aus Platte und Kontaktvolumen hat eine andere Lastausbreitung, sodass der Ansatz aus Formel 3.2 im FEM-Modell nicht in der Form gültig ist. Es müsste hier wahrscheinlich am realen Beispiel oder an einem erweiterten FEM-Modell untersucht werden, welche der beiden Lösungen der Realität eher entspricht.
Was jedoch zu beachten ist: Die Restklemmkraft ist in beiden Varianten nahezu identisch. Die Vorspannung in der Verbindung wird demnach gut abgebildet und kann für Untersuchungen an Anschlüssen verwendet werden.
Zusammenfassung
Die Modellierung einer vorgespannten Schraubenverbindung mit Hilfe von Kontaktvolumen, Flächen und Balkenstäben ist eine Mischung aus praktikabler Lösung und realer Abbildung. Praktikabel meint hier, dass der Rechenaufwand gegenüber einer Berechnung mit FEM-Volumen, welche die Verbindung wohl genauer abbilden würden, wesentlich geringer ausfällt. Es müssen dadurch aber Abstriche bei der Schraubenbemessung gemacht werden beziehungsweise muss hier noch eine weiterführende Untersuchung durchgeführt werden, welche die Ergebnisse zur Realität ins Verhältnis setzt.
Da die Vorspannkräfte und Restklemmkräfte weitestgehend mit denen aus der analytischen Rechnung übereinstimmen, ist davon auszugehen, dass diese Art der Modellierung für die Untersuchung von Anschlüssen durchaus zu Rate gezogen werden kann.