Modélisation d'un assemblage par boulon précontraint

Principes de base du diagramme des assemblages

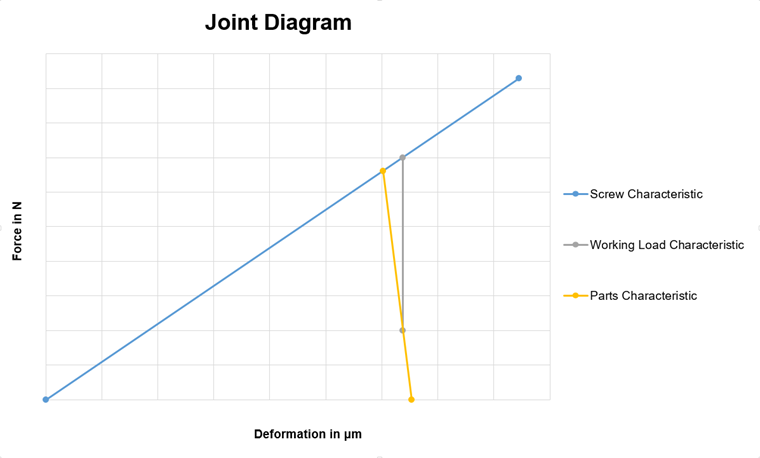
Le diagramme d'assemblage est une représentation graphique des efforts dans un assemblage boulonné précontraint. Les efforts de compression dans les composants à connecter et les déformations associées sont ici comparés aux efforts et aux déformations dans le boulon. La Figure 01 montre ce type de diagramme.

La ligne bleue (ligne caractéristique) représente le graphique du boulon, la ligne jaune un graphique des composants structurels. La rigidité des boulons est généralement inférieure à la rigidité des composants structuraux. Cependant, il existe également diverses exceptions, telles que les écrous. L'intersection des deux lignes représente la force de précontrainte dans la connexion sans charge externe appliquée. Le point d'extrémité de la ligne du boulon représente la force de résistance maximale dans le filetage.

Outre la ligne de boulon et la ligne du composant, il existe une autre ligne caractéristique importante de l'effort de traction externe (également précontrainte). Cette ligne est affichée en gris sur la Figure 01. Elle tire son origine de la ligne caractéristique des composants sur l'axe y de la force de serrage résiduelle souhaitée. La force de serrage résiduelle est la force qui maintienne les composants ensemble. Par exemple, si un effort horizontal doit être absorbé par l'assemblage (sans déformation de cisaillement du boulon, donc uniquement par la friction du composant) en plus du composant de traction dans le cas de la charge de travail existante, alors l'effort de serrage résiduel doivent être sélectionnés de manière à ce que la résistance soit suffisante.

Outre ces lignes caractéristiques, il existe d'autres lignes qui peuvent être utilisées pour une représentation plus détaillée. Ces lignes n'ayant aucune influence sur la procédure de base, elles ne seront cependant pas expliquées plus en détail dans cet article et seul le diagramme d'assemblage simplifié présenté ici sera utilisé. Par exemple, les lignes caractéristiques supplémentaires seraient dues à l'ensemble de compression ou à la contrainte et à la charge excentriques.

Formules du diagramme d'assemblage simplifié

Pour créer le diagramme d’assemblage, vous devez d’abord calculer les rigidités, déformations et efforts correspondants. En général, les rigidités de ressort peuvent être calculées selon la loi de Hooke comme suit:

Où
c = rigidité (constante de ressort)
F = force de ressort
f = déformation (flèche).

Dans le cas d'une barre en traction avec un matériau isotrope, la constante de ressort peut être calculée directement à l'aide du module d'élasticité (module d'élasticité) :

Où
E = module d'élasticité
A = aire de la section de la barre en traction
l est la longueur de la barre de traction.

La rigidité du boulon est simplifiée et seule la tige du boulon est appliquée. D'autres possibilités consiste à appliquer la tête de boulon, le filetage, l'écrou, différents diamètres de tige, etc. Dans ce cas, les éléments avec leur valeur réciproque sont ajoutés à la rigidité totale. La rigidité de ressort du boulon est calculée à l'aide de la formule suivante (index S) :

Où
c_S = rigidité de ressort des boulons
E_S = module d'élasticité du boulon
A_S = aire de la section du boulon
l_K est la longueur de serrage (hauteur/épaisseur des composants).

Le diamètre de la paroi du filetage d₃ est utilisé pour l'aire de la section dans la plage de filetage des boulons. Ainsi, la formule complète est obtenue comme suit :

La rigidité du composant est calculée de manière similaire. Comme il existe une plaque ou plusieurs, l'index P est utilisé :

Où
c_P = rigidité de ressort des composants/plaques
E_P = module d'élasticité des plaques
A_P = aire de la section des plaques
l_K est la longueur de serrage (hauteur/épaisseur des composants).

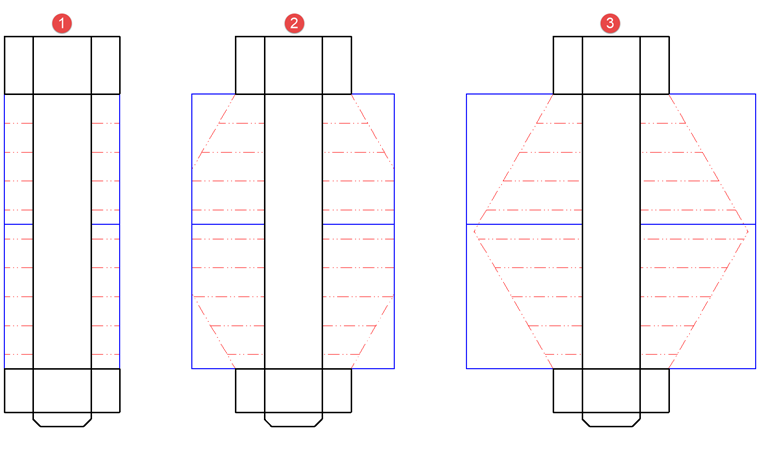
L'aire de la section A_P dépend de l'épaisseur, contrairement à la vis. Nous supposons que la charge est appliquée à un angle d'environ 60°. Comme le montre la Figure 02, trois cas sont possibles.

Dans le cas 1, les composants entre le boulon et l'écrou sont comme un mandrin et ce diamètre de mandrin est maximal égal au diamètre de la surface portante du boulon ou de l'écrou.
Le Cas 2 couvre la plage où ce diamètre de mandrin est à peu égal au diamètre de la surface portante de l'écrou ou du boulon et au maximum au diamètre du cône d'extension de charge (en rouge sur la Figure 02). Celle-ci s'étend symétriquement des deux côtés et son diamètre est le plus grand au milieu de la longueur de serrage.
Le Cas 3 couvre toute la plage qui va de l’extension de charge maximale en cône à l’extension de plaque infinie. Il est donc nécessaire de calculer l'aire de remplacement A_ers. Un_ers correspond à l'aire de la section d'un cylindre de remplacement avec une extension de charge constante.

Pour l'exemple suivant, le cas 3 est suffisant. A_ers est calculé à l'aide de la formule suivante (voir la VDI 2230, édition 1986 [1] ) :

Où
d_W = diamètre de la surface portante
d_h = diamètre du forage

Le diamètre de la surface portante peut être appliqué de manière simplifiée comme 90 % de la largeur sur les plaques :
d_W = 0,9 ∙ s (3,3)
Où
s est la largeur sur un plat de la tête/l'écrou du boulon.

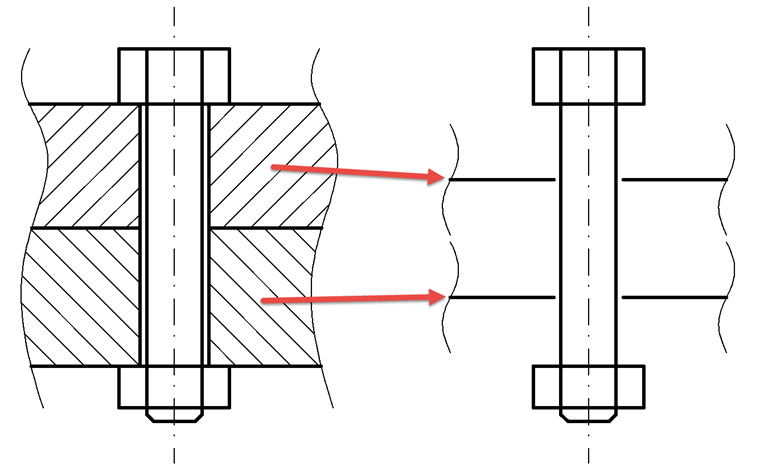
Étant donné que le point d’application de la charge dans un modèle surfacique n’est pas nécessairement au sommet du composant (la plaque), mais toujours au centre de la surface, la rigidité de la plaque doit être déterminée au niveau de ce point d’application de charge. Pour ce faire, le facteur d'application de charge n est introduit, ce qui réduit la longueur de serrage en conséquence. Ce problème est illustré sur la Figure 03.

Les composants réels (deux plaques, dans ce cas) sont réduits au centre des surfaces. Dans le cas de deux plaques, n est toujours égal à 0,5, car la moitié de chaque plaque est toujours utilisée. La nouvelle rigidité de plaque c_Pn est ensuite calculée comme suit :

Où
Φ_K = rapport de charge.

Outre les rigidités, les efforts internes sont néanmoins nécessaires pour créer des lignes caractéristiques. La charge de serrage résiduelle F_KR, la charge de travail F_A et le facteur de serrage α_A (serrage contrôlé par l'angle) doivent être définis. En revanche, les efforts d'assemblage résultants F_Mmin et F_Mmax doivent être calculés. Voici la formule des précontraintes de l'assemblage pour un serrage contrôlé par l'angle :
F_Mmin = F_Kmin + F_AP (3,6)
F_Mmax = α_A ∙ F_Mmin (3,7)
Où
α_A est le facteur de serrage pour la méthode basée sur l'angle
F_{Kmin =} force de serrage résiduelle minimum requise dans l’assemblage
_FPA est la charge de plaque supplémentaire due à la charge de travail.

La charge de plaque supplémentaire_FPA est la force qui s'exerce sur la charge de travail. Celle-ci est calculée selon la formule :
F_AP = (1 - n ∙ Φ_K ) ∙ F_A (3,8)
Où
F_A est la charge de travail.

Dans la simplification qui ne considère pas les tassements, la force de précontrainte F_V correspond à la force de précontrainte minimale F_Mmin. Pour considérer la ligne de charge de travail, il manque l'effort de traction maximal F_Smax qui apparaît dans le boulon au niveau de la charge de travail :
F_Smax = F_Mmax + F_SA (3,9)
Où
F_SA représente l'effort supplémentaire appliqué aux boulons.

L'effort additionnel F_SA est à nouveau calculé de la même manière que la formule 3.8 :
F_SA = n∙ Φ_K ∙ F_A (3,10)

La capacité de charge maximale du boulon (F_0,2 ) en tant que dernière force manquante doit être déterminée à l'aide de l'aire de section du boulon dans le filetage. Celle-ci est calculée à l'aide du diamètre de l'aire de la section d_s, qui résulte de la valeur moyenne du diamètre du noyau d_k (d₃ ) et du diamètre de la semelle d_fl (d₂ ) :

Où
d₂ = diamètre de la semelle du filetage
d₃ = diamètre central du filetage
f_ub est la résistance en traction du matériau des pièces de fixation.

Outre les efforts, les déformations doivent être déterminées sous forme de valeurs correspondantes afin que les lignes caractéristiques puissent être entrées dans le diagramme d'assemblage. Pour ce faire, la formule 1.1 convertie selon f est utilisée. Voici les formules des déformations f par rapport aux efforts respectifs F :

On obtient ainsi les points de ligne/valeurs suivants pour le diagramme d'assemblage :

Ligne caractéristique	déformation	Force
Boulon	0	0
	f0,2	f0,2
Plaque	fSMmax	fMmax
	fSMmax + fPMmax ou fMmax	0
Charge de service	fSMmax + fSA	FMmax − FAP
	fSMmax + fSA	FMmax + FSA = FSmax

Tableau 1 – Points/valeurs de ligne pour le diagramme d’assemblage

Modélisation d'un assemblage par boulon précontraint dans RFEM

Le modèle doit être un bon mélange de précision et de fonctionnalité. Par conséquent, l'assemblage sera composé de surfaces, de barres et de solides de contact.

Les paramètres suivants sont définis pour l'exemple de calcul :
F_A = 25 kN
F_K = 10 kN
E_S = E_P = 210 000 N/mm²
t₁ = t₂ = 10 mm
l_K = t₁ + t₂ = 20 mm
d_h = 10 mm
d_A > d_W + l_K
n = 0,5
α_A = 1,0

Boulon :
M10 8,8
f_ub = 800 N/mm²
d₂ = 9,03 mm
d₃ = 8,16 mm
s = 17 mm

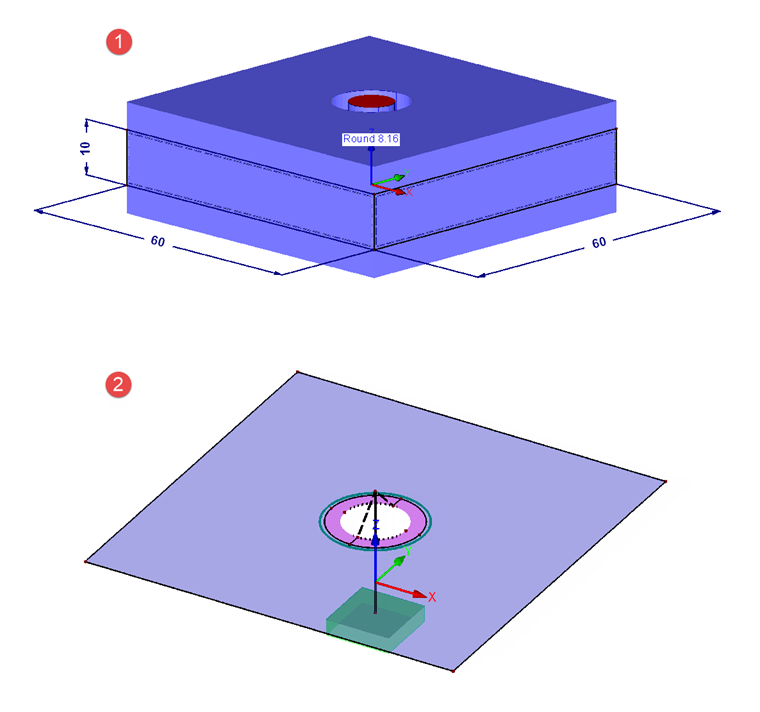
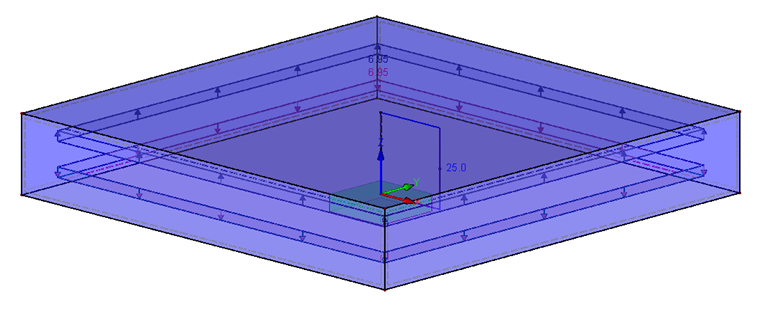
Le modèle comprend deux surfaces carrées superposées avec un trou (diamètre d_h ) au centre, qui ont des dimensions 60 x 60 mm (pour remplir D_A > d_W + l_K ). Comme t₁ = t₂, l’espacement des plaques est de 10 mm. La charge agit directement au centre du centre de la plaque ( fibre neutre ). Le n résultant est ainsi de 0,5. Le modèle est supporté par un appui fixe à l'extrémité inférieure de la barre du boulon. Pour obtenir une force d'appui totale égale à zéro, la charge doit être appliquée à la fois aux plaques supérieure et inférieure. La charge appliquée est de 6,95 N/mm² pour un effort total de 25 kN.

Pour un bon transfert de charge entre le boulon (poutre) et les plaques, une surface rigide (anneau) de diamètre extérieur d_W est modélisée autour du trou. La connexion entre les plaques est générée à l'aide de trois solides de contact. Un solide se trouve autour du trou sans la partie surfacique rigide ; deux solides de contact reposent autour du trou comme deux coques. Les solides de contact doivent avoir le même matériau que les plaques afin de représenter avec précision la rigidité entre les plaques. De plus, le contact est en échec lors du soulèvement et il y a une friction rigide dans la direction horizontale avec le facteur de 0,1.

La structure est affichée sur la Figure 04. Le numéro 1 affiche les surfaces et les barres avec leurs dimensions réelles. Le numéro 2 affiche la surface supérieure avec la poutre ( boulon ) et les barres rigides, qui représentent la connexion entre le boulon et la plaque. La surface rigide (en rose) a également une barre rigide sur le bord intérieur pour pouvoir transférer les moments.

Le maillage EF est un autre aspect important. La taille du maillage EF principal pour l_EF a été définie sur 2 mm en raison de ces petites dimensions. De plus, le raffinement du maillage surfacique a été défini avec l_EF 0,2 mm sur les surfaces rigides.

Étant donné que le diamètre et la force de travail des boulons ne sont pas connus, il est possible de modéliser la structure sans le trou et d'utiliser une barre rigide au lieu d'une poutre pour la première vérification du modèle et pour la détermination du sur les boulons. Ce modèle pour le prédimensionnement est illustré dans la Figure 05.

Une barre résultante a été fixée parallèle au boulon (distance de 0,1 mm) afin de pouvoir détecter la précontrainte résiduelle sur le modèle. Cela inclut tous les efforts internes du solide de contact.

Comparaison des solutions analytiques et numériques

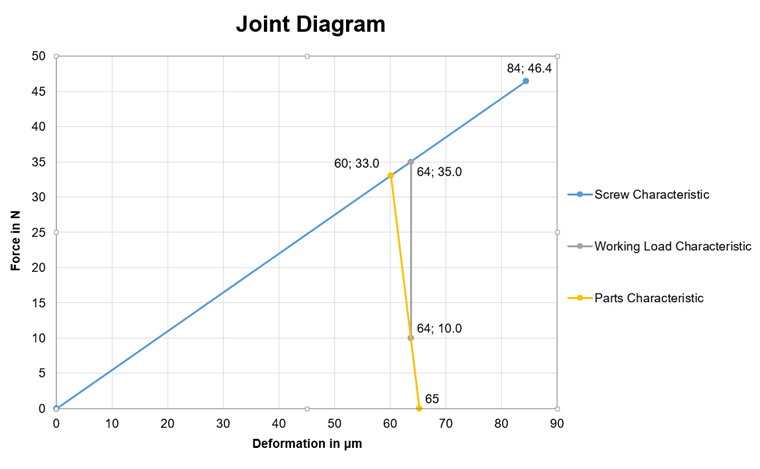
Pour comparer les solutions, vous devez d'abord créer le diagramme d'assemblage. Les valeurs requises sont listées dans le Tableau 1. Les valeurs intermédiaires et les lignes caractéristiques indiquées dans le Tableau 2 sont obtenues en substituant les valeurs à l'exemple pratique (voir ci-dessus). Le Tableau 3 contient un résumé des valeurs les plus importantes analogues au Tableau 1 et la Figure 06 montre le diagramme d'assemblage complet.

Symbole	Numéro de la formule	Valeur
cS	2,2	549 kN/mm
As	3.2	303 mm²
cP	3,1	3 182 kN/mm
ΦK	3,5	0,147
cPn	3,4	6 921 kN/mm
fSA	3.10	1,8 kN
fSA	4.4	3 µm
FAP	3.8	23,2 kN
fMmax	3,6, 3,7	33,2 kN
fSMmax	4.2	60 µm
fMmax	4.3	65 µm
f0,2	3,11	46,2 kN
f0,2	4.1	84 µm

Tableau 2 – Résultats intermédiaires et résultats de l’exemple de calcul

Ligne caractéristique	Déformation [μm]	Force [kN]
Boulon	0	0,0
	84	46,2
Plaque	60	33,2
	65	33,2
Charge de service	63	10.0
	63	35,0

Tableau 3 – Points/valeurs caractéristiques de l’exemple de calcul

Deux cas de charge ont été initialement créés pour la solution numérique. Le premier cas de charge (Précontrainte CC1) inclut la charge de barre de la précontrainte et le deuxième cas (Charge de travail CC2) inclut la charge de travail. De plus, la combinaison de charges des deux cas de charge (facteur 1,0) a été générée (CO1 : CC1 + CC2). Le calcul est basé sur une analyse statique linéaire avec 15 pas de charge (une meilleure convergence dans le cas des solides de contact en échec).

Pour la précontrainte, vous avez la possibilité d'appliquer le type de charge de barre précontrainte initiale ou précontrainte finale à la barre. La précontrainte réelle est la précontrainte finale. Étant donné que la charge de précontrainte finale nécessite beaucoup de temps de calcul, il est recommandé d'utiliser la charge de barre de précontrainte initiale. Cependant, cette charge a le défaut de ne pas inclure la force de réaction traversant les plaques. L’effort normal dans la barre est donc trop faible après le calcul, car une partie peut être réduite par déformation des plaques. Cette différence peut être réduite de deux manières. Celle-ci peut être prévue à l'aide de la déformation de la plaque et convertie en force supplémentaire F_{Zus, v} (calculée) selon la formule suivante :
F_Zus,v = f_PMmax ∙ c_S (5,1)

Toutefois, cette valeur peut également être déterminée itérativement. Pour ce faire, le cas de charge précontraint doit être calculé. La différence entre la précontrainte initiale appliquée et l'effort normal résultant dans la barre correspond à l'effort additionnel F_Zus,i (itératif). La formule suivante peut être utilisée :
F_Zus,i = F_Mmax - N_S (5,2)
Où
N_S est l'effort normal dans la barre à la précontrainte initiale F_Mmax.

La force additionnelle F_Zus,v résulte des valeurs du Tableau 2 comme suit :
F_Zus,v = f_PMmax ∙ c_S = (f_Mmax - f_SMmax ) ∙ c_S = 5 μm ∙ 549kN/mm = 2,8 kN

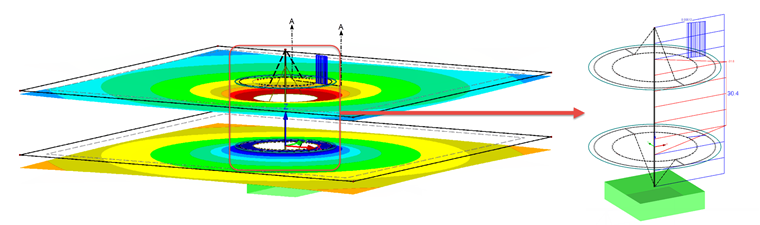
La force supplémentaire itérative F_Zus,i peut être obtenue après avoir calculé le cas de charge sur la barre dans la Figure 07.

F_Zus,i = 33,2 kN - 30,4 kN = 2,8 kN

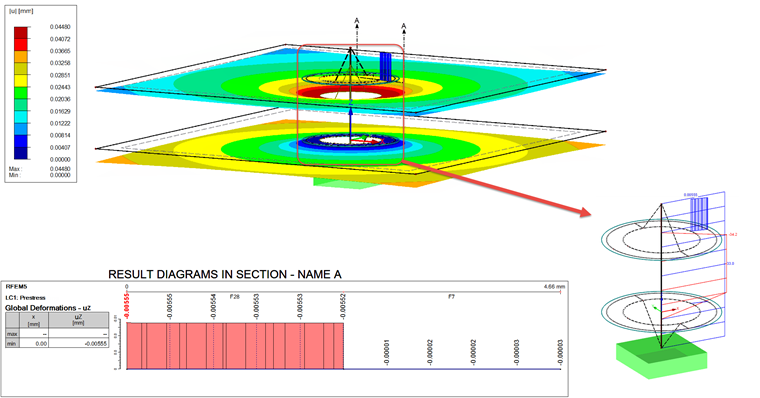
La précontrainte résultante est ainsi de 36 kN dans les deux cas. Le cas de charge peut ainsi être recalculé. Le résultat est illustré sur la Figure 08.

La barre résultante supplémentaire, qui additionne les efforts de contact de tous les solides de contact, a un résultat de 34,2 kN. C'est environ 1,2 kN de plus que l'effort normal de la barre de boulon, qui est de 33 kN. La déformation des deux surfaces (S1 et S27) affichée dans le diagramme doit être ajoutée pour pouvoir la comparer avec f_PMmax. En moyenne, les résultats sont les suivants :

La déformation est ainsi 0,6 μm supérieure à la déformation calculée f_Mmax.

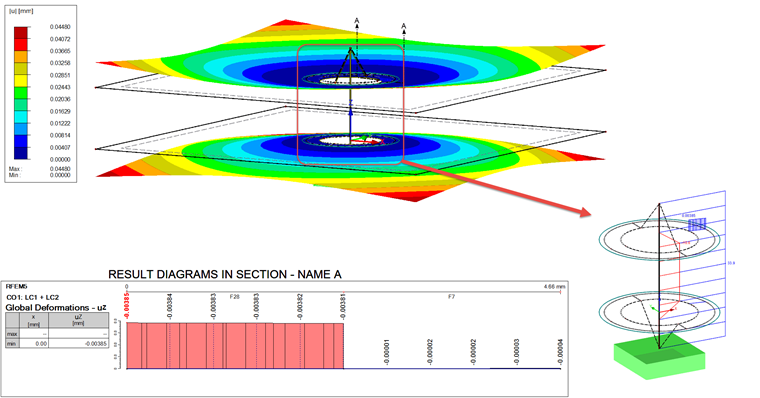
Le résultat des calculs soumis à la charge de travail dans le CC1 est affiché sur la Figure 09.

Le boulon a un résultat de 33,9 kN. Cette force de barre peut être comparée à la force F_Smax = 35 kN (voir les Tableaux 1 et 3, Charge de travail). La différence est de 1,1 kN. L’écart des différences est également important ici. D'après le calcul analytique, la différence doit être égale à la force F_SA = 1,8 kN. Cependant, la différence du modèle EF n'est pas aussi grande, avec 33,9 kN − 33 kN = 0,9 kN.

Des écarts similaires sont obtenus dans le cas d'une déformation (voir le diagramme de la Figure 09). La valeur indiquée représente la valeur réduite de la charge de travail. La déformation doit donc être calculée par la charge de service à l'aide de la déformation par la précontrainte. La déformation réelle est la différence entre u_z,1 et la déformation moyenne dans le diagramme. La valeur de référence analytique est f_SA. On obtient ainsi la déformation u_z,2 :

La déformation est ainsi inférieure d'environ 1,4 μm à la déformation calculée f_Mmax.

Enfin, les résultats dans la barre résultante sont comparés. Comme vous pouvez le voir sur la Figure 09, la charge de la barre résultante est une force de compression de 10,6 kN. Cette valeur doit être comparée avec la charge de serrage F_K = 10 kN. On obtient un écart de 0,6 kN. Le tableau 4 comprend un résumé de tous les résultats.

Symbole	Analytique Valeur	Calcul par MEF		Écart
		barre	Plaque
fMmax [kN]	33,2	33,0	34,2	0,2/1,2
fPMmax [μm]	5.0	-	5.6	0,6
fSA [μm]	3,0	-	1,6	1,4
FMmax +FSA [kN]	35,0	33,9	-	1,1
FMmax - FAP [kN]	10.0	-	10,6	0,6

Tableau 4 – Valeurs de comparaison du modèle analytique/calcul aux éléments finis

Évaluation

Comme le montre le Tableau 4, il existe des différences partiellement importantes entre les modèles. Les correspondances les plus larges se trouvent généralement dans le cas de charge Précontrainte. Selon l'évaluation de la barre résultante (plaque) ou de la barre boulonnée, les écarts par rapport à F_Mmax sont de 3,6 % ou 0,6 % (par rapport au résultat analytique).

Le plus grand écart est dû à la déformation de la barre et de la plaque après application de la charge de travail. Dans ce cas, il existe un écart de 1,1 kN entre l'effort normal sur la barre et la solution analytique. Cet écart est initialement de 3 % pour la solution analytique. Cependant, la différence est bien plus grande lorsque l'on se réfère à l'effort additionnel du boulon. L'écart du modèle aux éléments finis est le suivant :
F_SA,FEM = (F_Mmax + F_SA ) - F_Mmax = 33,9 kN - 33 kN = 0,9 kN | 1,8 kN = F_SA

Ces écarts peuvent être causés par le fait que les deux plaques n'ont pas de rigidité dans la direction z et que le solide de contact n'a qu'un élément EF dans son épaisseur. Ainsi, il ne peut pas y avoir d'extension de charge à l'intérieur du solide. Le transfert de charge dans le solide s'effectue exclusivement via la déformation de la plaque par flexion et effort tranchant. Les valeurs montrent que le modèle EF dans le cas de charge Précontrainte dans la combinaison de plaques et de solides de contact a une rigidité plus faible que dans le modèle analytique (voir la déformation plus petite). À ce stade, la rigidité plus élevée du boulon peut être exclue, car elle est déterminée par la théorie de la poutre et la section.

En revanche, la déformation est plus faible dans le cas de la combinaison de charges dans le modèle aux éléments finis ou l'effort sur les boulons est affiché avec un incrément beaucoup plus faible. Cela indique également la rigidité plus élevée dans la plaque. En résumé, il n'y a qu'une explication à ce problème : Le modèle composite constitué d'une plaque et d'un solide de contact a une extension de charge différente, l'approche de la formule 3.2 dans le modèle aux éléments finis n'est donc pas valide dans ce cas. Il serait probablement nécessaire d'examiner un exemple réel ou un modèle d'analyse aux éléments finis étendu pour trouver la solution la plus proche de la réalité.

Cependant, il est important de noter que La force de serrage résiduelle est presque identique dans les deux variantes. La précontrainte dans l’assemblage est ainsi modélisée et peut être utilisée pour l’analyse des assemblages.

Résumé

La modélisation d’un assemblage boulonné précontraint à l’aide de solides de contact, de surfaces et de poutres est une combinaison de solution pratique et d’affichage réel. En pratique, le temps de calcul est considérablement plus petit, par rapport au calcul avec les solides EF, qui représenteraient probablement l'assemblage avec plus de précision. Cependant, il est nécessaire d'améliorer la vérification des boulons ou d'effectuer une analyse plus approfondie afin de définir les résultats par rapport à la réalité.

Étant donné que les efforts de précontrainte et les efforts de serrage résiduels correspondent en grande partie à ceux du calcul analytique, on suppose que ce type de modélisation peut être utilisé pour l'analyse des assemblages.

Littérature

[1]	Association des ingénieurs allemands : (1986). Ligne directrice VDI 2230 – Calcul systématique des assemblages boulonnés soumis à de fortes contraintes Berlin : Beth, 1993