Basics of Joint Diagram
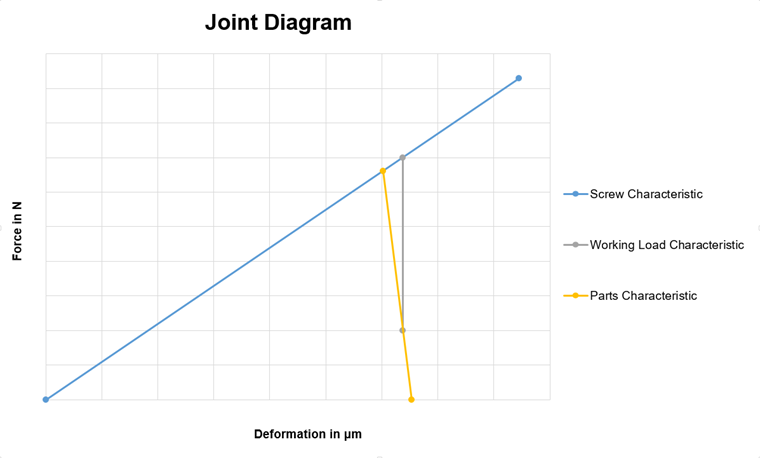
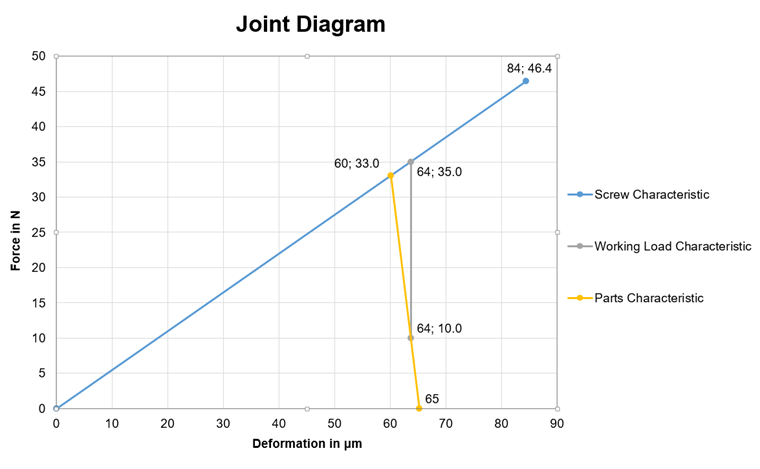
The joint diagram is a graphical representation of forces in a prestressed bolt connection. In this case, the compression forces arising in the components to be connected and the accompanying deformations are contrasted with the forces and deformations in the bolt. Image 01 shows such a diagram.
The blue line (characteristic line) represents a graph of the bolt, the yellow one a graph of the structural components. Typically, the bolt stiffness is smaller than the stiffness of the structural components. However, there are also various exceptions such as in the case of nuts. The intersection of both lines represents the preloading force in the connection without an external load applied. The end point of the bolt line is the maximum resistance force in the thread.
In addition to the bolt line and the component line, there is another important characteristic line of the external tensile force (also preload). This line is shown in gray in Image 01. It originates from the characteristic line of the components on the y-axis of the desired residual clamping force. The residual clamping force is the force that still holds the components together. For example, if there is a horizontal force to be absorbed by the connection (without shear strain of the bolt, so only by the component friction) in addition to the tensile component in the case of the existing working load, then the residual clamping force must be selected in a way that there is sufficient resistance.
In addition to these characteristic lines, there are other lines that can be used for a more detailed representation. However, since these lines have no influence on the basic procedure, they will not be explained further in this article, and the presented simplified joint diagram will only be used. For example, the additional characteristic lines would be due to the compression set or the eccentric stress and load.
Formulas of Simplified Joint Diagram
In order to create the joint diagram, it is necessary to calculate the corresponding stiffnesses, deformations, and forces first. In general, the spring stiffnesses can be calculated according to the Hooke's law as follows:
where
c is the stiffness (spring constant),
F is the spring force,
f is the deformation (deflection).
In the case of a tension member with isotropic material, the spring constant can be calculated directly using the elastic modulus (modulus of elasticity):
where
E is the elastic modulus,
A is the cross-section area of the tension member,
l is the length of the tension member.
The bolt stiffness is simplified and only the bolt shaft is applied. Other options are to apply the bolt head, thread, nut, different shaft diameters, and so on. In that case, the elements with their reciprocal value are added to the total stiffness. The spring stiffness of the bolt is calculated using the following formula (Index S):
where
cS is the spring stiffness of the bolt,
ES is the elastic modulus of the bolt,
AS is the cross-section area of the bolt,
lK is the clamping length (height/thickness of the components).
The thread flank diameter d3 is used for the cross-section area in the bolt thread range. Thus, the total formula results:
The component stiffness is calculated in a similar way. Since there is one plate or more, the index P is used:
where
cP is the spring stiffness of the components/plates,
EP is the elastic modulus of the plates,
AP is the cross-section area of the plates,
lK is the clamping length (height/thickness of the components).
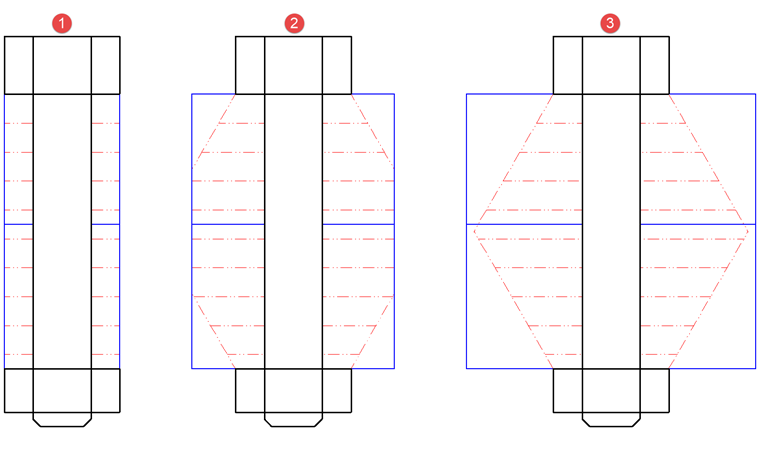
The cross-section area AP depends on the thickness, in contrast to the bolt. It is assumed that the load is extended at an angle of approximately 60°. There are three different cases, as shown in Image 02.
In Case 1, the components between the bolt and the nut are like a sleeve, and this sleeve diameter is maximally equal to the bearing surface diameter of the bolt or nut.
Case 2 covers the range where this sleeve diameter is minimally equal to the bearing surface diameter of the nut or bolt, and maximally equal to the diameter of the load extension cone (marked red in Image 02). This stretches symmetrically from both sides, and the diameter is the largest in the middle of the clamping length.
Case 3 covers the range from the maximum load extension cone to the infinite plate extension. For this reason, it is necessary to calculate the replacement area Aers. Aers corresponds to the cross-section area of a replacement cylinder with a constant load extension.
For the following example, Case 3 is sufficient. Aers is calculated using the following formula (see VDI 2230, edition 1986 [1]):
where
dW is the bearing surface diameter,
dh is the bore diameter.
The bearing surface diameter can be applied in a simplified way as 90% of the width across flats:
dW = 0.9 ∙ s (3.3)
where
s is the width across flats of the bolt head/nut.
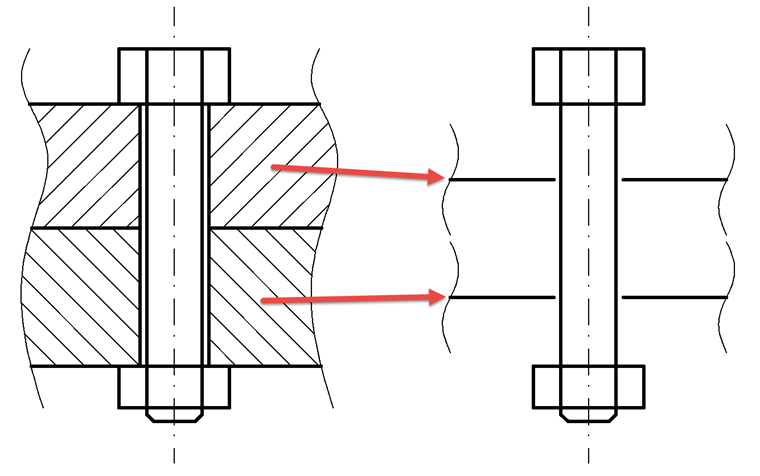
Since the load application point in a surface model is not necessarily at the top of the component (the plate), but always in the middle of the surface, the plate stiffness must be determined on this load application point. For this, the load application factor n is introduced, which reduces the clamping length accordingly. This problem is illustrated in Image 03.
The actual components (two plates, in this case), are reduced to the middle of the surfaces. In the case of two plates, n is always 0.5, as half of each plate is always used. The new plate stiffness cPn is then calculated as follows:
where
ΦK is the load ratio.
To create the characteristic lines, various forces are still required, in addition to stiffnesses. The residual clamping load FKR, the working load FA, and the tightening factor αA (angle-controlled tightening) must be specified. The resulting minimum and maximum assembly forces FMmin and FMmax, in contrast, must be calculated. Below is the formula for the assembly preloads at an angle-controlled tightening:
FMmin = FKmin + FPA (3.6)
FMmax = αA ∙ FMmin (3.7)
where
αA is the tightening factor for the angle-controlled method,
FKmin is the minimum required residual clamping force in the connection,
FPA is the additional plate load due to the working load.
The additional plate load FPA is the force arising when applying the working load. It is calculated according to the formula:
FPA = (1 - n ∙ ΦK) ∙ FA (3.8)
where
FA is the working load.
In the simplification without considering settlements, the prestressing force FV corresponds to the minimum prestressing force FMmin. To consider the working load line, the maximum bolt force FSmax is missing, which arises in the bolt when concerning the working load:
FSmax = FMmax + FSA (3.9)
where
FSA is the additional bolt force.
The additional bolt force FSA is again calculated similarly to Formula 3.8:
FSA = n∙ ΦK ∙ FA (3.10)
The maximum loading capacity of the bolt (F0.2) as the last missing force must be determined using the cross-section area of the bolt in the thread. This is calculated using the cross-section area diameter ds, which results from the mean value of the core diameter dk (d3) and the flank diameter dfl (d2):
where
d2 is the flank diameter of the thread,
d3 is the core diameter of the thread,
fub is the tensile strength of the bolt material.
In addition to the forces, the deformations must be determined as the corresponding values so the characteristic lines can be entered in the joint diagram. For this, Formula 1.1 converted according to f is used. Below are the formulas for the deformations f to the respective forces F:
This results in the following line points/values for the joint diagram:
| Characteristic Line | Deformation | Force |
|---|---|---|
| Bolt | 0 | 0 |
| f0,2 | F0,2 | |
| Plate | fSMmax | FMmax |
| fSMmax + fPMmax or fMmax | 0 | |
| Working load | fSMmax + fSA | FMmax − FPA |
| fSMmax + fSA | FMmax + FSA = FSmax |
Table 1 – Line Points/Values for Joint Diagram
Modeling Prestressed Bolt Connection in RFEM
The model should be a good mix of accuracy and practicability. Therefore, the connection will consist of surfaces, members, and contact solids.
The following parameters are specified for the calculation example:
FA = 25 kN
FK = 10 kN
ES = EP = 210,000 N/mm²
t1 = t2 = 10 mm
lK = t1 + t2 = 20 mm
dh = 10 mm
DA > dW + lK
n = 0.5
αA = 1.0
Bolt:
M10 8.8
fub = 800 N/mm²
d2 = 9.03 mm
d3 = 8.16 mm
s = 17 mm
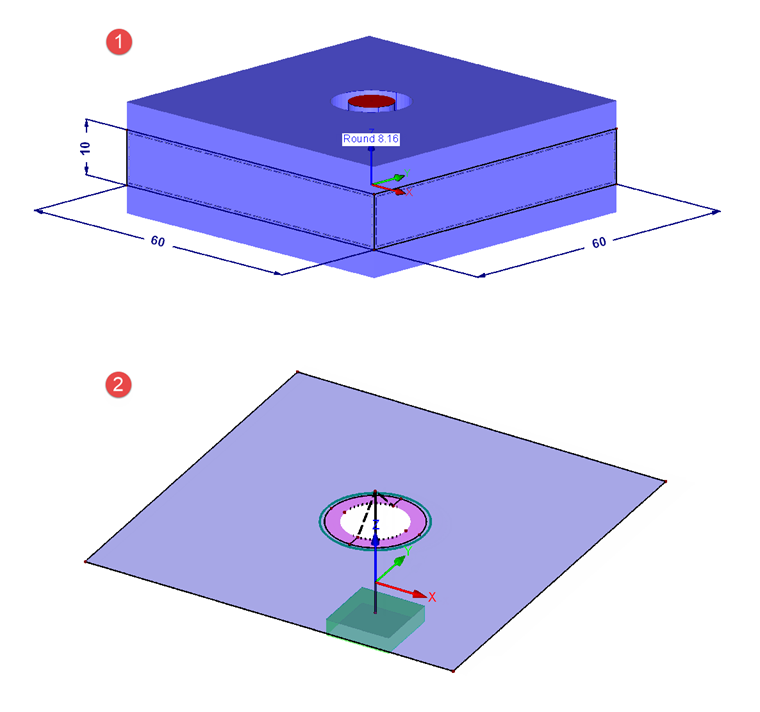
The model includes two superimposed square surfaces with a hole (diameter dh) in the middle, which have the dimensions 60 x 60 mm (to fulfil DA > dW + lK). Since t1 = t2, this results in a plate spacing of 10 mm. The load acts directly in the middle of the plate (neutral fiber). Thus, the resulting n is 0.5. The model is supported by a fixed support at the bottom end of the bolt member. In order to achieve a total support force equal to zero, the load must be applied to both the upper and the bottom plates. The load is 6.95 N/mm² for 25 kN of the total force.
For a good load transfer between the bolt (beam) and plates, a rigid surface (ring) with the outer diameter dW is modeled around the hole. The connection between the plates is generated using three contact solids. One solid is around the hole without the rigid surface part; two contact solids rest around the hole like two shells. The contact solids must have the same material as the plates to reflect the stiffness between the plates accurately. Furthermore, the contact fails when lifting, and it has a rigid friction in the horizontal direction with the factor of 0.1.
The structure is displayed in Image 04. Number 1 shows the surfaces and members with the actual dimensions. Number 2 shows the upper surface with the beam (bolt) and the rigid members, which represent the connection between the bolt and the plate. The rigid surface (pink) also has a rigid member on the inner edge to be able to transfer any moments.
Another important point is the FE mesh. Due to the small dimensions, the main FE mesh size for lFE has been set to 2 mm. Moreover, the surface mesh refinement has been defined with lFE 0.2 mm on the rigid surfaces.
Since neither the bolt diameter nor the working force on the bolt is known in practice, it is possible to model the structure without the hole and to use a rigid member instead of a beam for the first design of the model and for the determination of the bolt forces. This model for pre-dimensioning is shown in Image 05.
In order to be able to detect the residual prestress in the model, a result member was attached parallel to the bolt (distance 0.1 mm). This includes all the internal forces of the contact solid.
Comparison of Analytical and Numerical Solutions
To compare the solutions, it is necessary first to create the joint diagram. The required values are listed in Table 1. The intermediate values and characteristic lines shown in Table 2 are obtained by substituting the values for the practical example (see above). Table 3 includes the summary of the most important values analogous to Table 1, and Image 06 shows the complete joint diagram.
| Symbol | Formula Number | Value |
|---|---|---|
| cS | 2.2 | 549 kN/mm |
| Aers | 3.2 | 303 mm² |
| cP | 3.1 | 3,182 kN/mm |
| ΦK | 3.5 | 0.147 |
| cPn | 3.4 | 6,921 kN/mm |
| FSA | 3.10 | 1.8 kN |
| fSA | 4.4 | 3 μm |
| FPA | 3.8 | 23.2 kN |
| FMmax | 3.6, 3.7 | 33.2 kN |
| fSMmax | 4.2 | 60 μm |
| fMmax | 4.3 | 65 μm |
| F0,2 | 3.11 | 46.2 kN |
| f0,2 | 4.1 | 84 μm |
Table 2 – Intermediate Results and Results of Calculation Example
| Characteristic Line | Deformation [μm] | Force [kN] |
|---|---|---|
| Bolt | 0 | 0.0 |
| 84 | 46.2 | |
| Plate | 60 | 33.2 |
| 65 | 33.2 | |
| Working load | 63 | 10.0 |
| 63 | 35.0 |
Table 3 – Characteristic Line Points/Values of Calculation Example
Two load cases were initially created for the numerical solution. The first load case (LC1 Prestress) includes the member load of the prestress, and the second case (LC2 Working load) includes the working load. Furthermore, the load combination of both load cases (factor 1.0) was generated (CO1: LC1 + LC2). The calculation is based on the linear static analysis with 15 load steps (better convergence in the case of contact solids with failure).
For the prestress, it is possible to apply the member load type initial prestress or end prestress to the member. The actual preload is the end prestress. Since the end prestress load requires a lot of computing time, we recommend using the member load of initial prestress. However, this has the disadvantage that this load does not include the reacting force through the plates. Therefore, the axial force in the member is too small after the calculation, since a part can be reduced by deformation of the plates. This difference can be reduced in two ways. On one hand, this can be predicted by means of the plate deformation and converted into an additional force FZus,v (predicted) according to the following formula:
FZus,v = fPMmax ∙ cS (5.1)
On the other hand, this can also be determined iteratively. For this, the prestress load case must be calculated. The difference between the applied initial prestress and the resulting axial force in the member corresponds to the additional force FZus,i (iterative). The following formula can be used:
FZus,i = FMmax - NS (5.2)
where
NS is the axial force in the member at initial prestress FMmax.
The additional force FZus,v results from the values in Table 2 as follows:
FZus,v = fPMmax ∙ cS = (fMmax - fSMmax) ∙ cS = 5 μm ∙ 549kN/mm = 2.8 kN
The iterative additional force FZus,i can be obtained after calculating the load case on the member in Image 07.
FZus,i = 33.2 kN - 30.4 kN = 2.8 kN
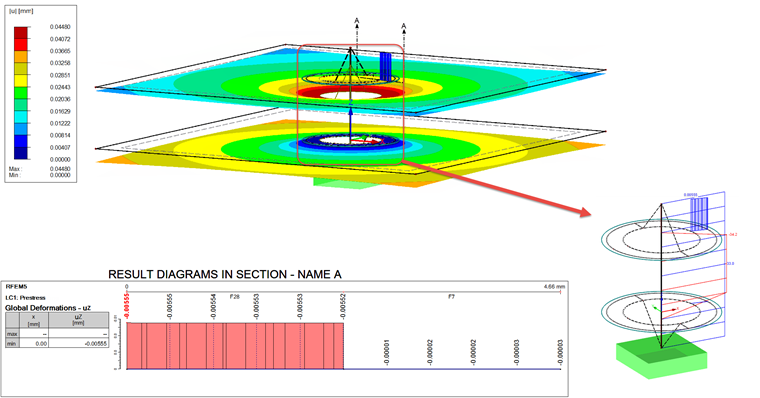
Thus, the resulting prestress is 36 kN in both cases. This allows for recalculation of the load case. The result is shown in Image 08.
The additional result member, which adds up the contact forces of all contact solids, has the result of 34.2 kN. This is about 1.2 kN more than the axial force of the bolt member, which is 33 kN. The deformation of both surfaces (S1 and S27) shown in the diagram must be added in order to be able to compare it with fPMmax. On average, this results as follows:
The deformation is thus 0.6 μm greater than the calculated deformation fMmax.
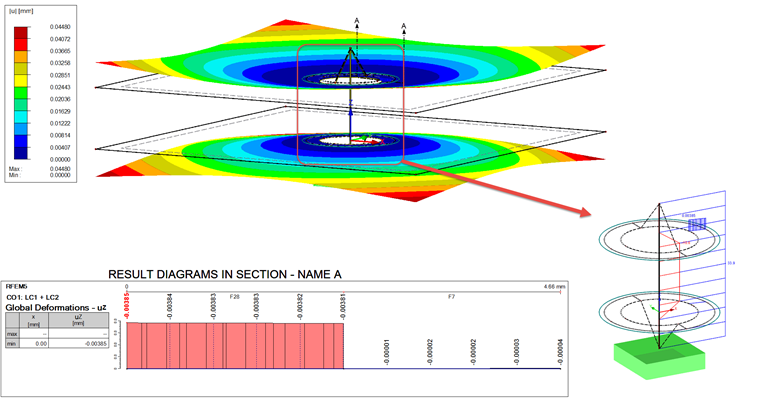
The result of the calculations subjected to the working load in LC1 is shown in Image 09.
The bolt member has the result of 33.9 kN. This member force can be compared to the force FSmax = 35 kN (see Table 1 and Table 3, Working Load). The difference is 1.1 kN. The deviation of the differences is also important here. According to the analytical calculation, the difference should be equal to the force FSA = 1.8 kN. However, the difference of the FE model is only half as great, with 33.9 kN − 33 kN = 0.9 kN.
Similar deviations are obtained in the case of deformation (see the diagram in Image 09). The value shown is the value reduced by the working load. Thus, the deformation must be calculated by the working load using the deformation by the prestress. The actual deformation is the difference between uz,1 and the mean deformation in the diagram. The analytical reference value is fSA. This results in the deformation uz,2:
Thus, the deformation is about 1.4 μm smaller than the calculated deformation fMmax.
Finally, the results in the result member are compared. As you can see in Image 09, the load for the result member is the compressive force of 10.6 kN. This value must be compared with the clamping load FK = 10 kN. This results in a deviation of 0.6 kN. Table 4 includes a summary of all the results.
| Symbol | Analytical Value | FEM Calculation | Deviation | |
|---|---|---|---|---|
| Member | Plate | |||
| FMmax [kN] | 33.2 | 33.0 | 34.2 | 0.2 / 1.2 |
| fPMmax [μm] | 5.0 | - | 5.6 | 0.6 |
| fSA [μm] | 3.0 | - | 1.6 | 1.4 |
| FMmax + FSA [kN] | 35.0 | 33.9 | - | 1.1 |
| FMmax - FPA [kN] | 10.0 | - | 10.6 | 0.6 |
Table 4 – Comparison Values of Analytical Model/FEM Calculation
Evaluation
As shown in Table 4, there are partially large differences between the models. Generally, the largest matches are in the Prestress load case. Depending on the evaluation of the result member (plate) or the bolt member, the deviations from FMmax are 3.6% or 0.6% (referred to the analytical result).
The largest deviation is the result of the bolt member and the plate deformation after applying the working load. In this case, there is a deviation of 1.1 kN between the axial force on the member and the analytical solution. This deviation, referred to the analytical solution, is initially 3%. However, the difference is much greater when referred to the bolt additional force. The deviation of the FEA model is as follows:
FSA,FEM = (FMmax + FSA) - FMmax = 33.9 kN - 33 kN = 0.9 kN << 1.8 kN = FSA
These deviations can be caused by the fact that both plates have no rigidity in the z-direction and the contact solid has only one FE element in its thickness. Thus, there can be no load extension within the solid. The load transfer in the solid is done exclusively via the deformation of the plate by bending and shear force. It is obvious from the values that the FE model in the Prestress load case in the combination of plates and contact solids has smaller stiffness than in the analytical model (see the smaller deformation). At this point, the higher stiffness of the bolt can be excluded, as this is determined by the beam theory and the cross-section.
On the other hand, there is a smaller deformation in the case of the load combination in the FEA model, or the bolt force has a significantly smaller increment. This, again, indicates the higher stiffness in the plate. In summary, there is only one explanation for this: The composite of a plate and contact solids has a different load extension, so the approach from Formula 3.2 in the FEA model is not valid in the form. It would likely be necessary to examine a real example or an extended FEA model to find out which solution is closer to reality.
However, it is important to note the following: The residual clamping force is almost identical in both variants. Thus, the prestress in the connection is modeled well and can be used for the joint analysis.
Summary
Modeling a prestressed bolt connection using contact solids, surfaces, and beams is a combination of a practical solution and real display. Practical means that the computing time is significantly smaller, compared to the calculation with FEA solids, which would probably represent the connection more accurately. However, it is necessary to improve the bolt design or to perform further analysis, which sets the results in relation with the reality.
Since the preloading forces and the residual clamping forces largely correspond to those from the analytical calculation, it can be assumed that this modeling type can be used for the connection analysis.