Modelação de uma ligação de parafuso pré-esforçada

Noções básicas do diagrama de ligação

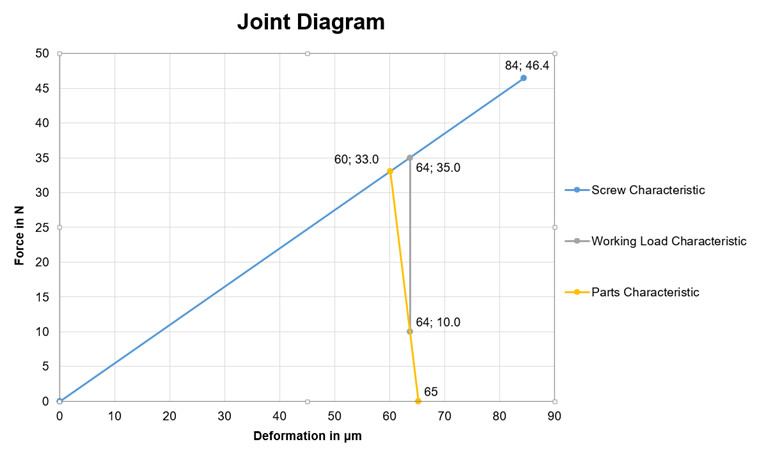
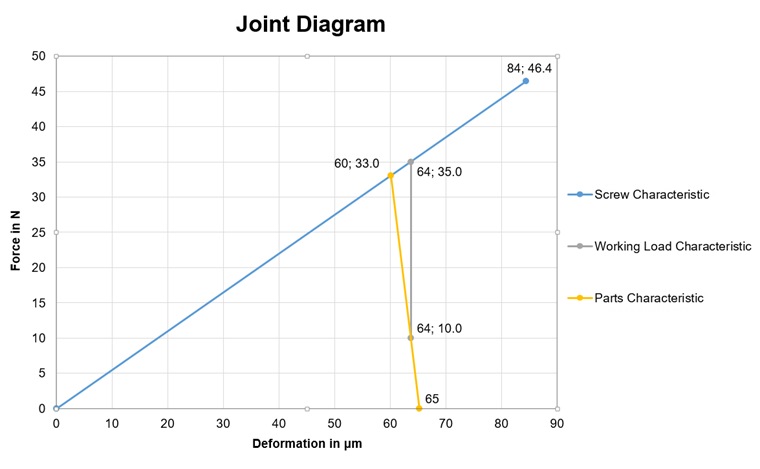
O diagrama de ligação é uma representação gráfica das forças numa ligação de parafuso pré-esforçada. Neste caso, as forças de compressão que surgem nos componentes a serem ligados e as respetivas deformações são comparadas com as forças e as deformações no parafuso. A Figura 01 mostra esse diagrama.

A linha azul (linha característica) representa o gráfico do parafuso, a linha amarela o gráfico dos componentes estruturais. Normalmente, a rigidez dos parafusos é inferior à rigidez dos componentes estruturais. No entanto, também existem várias exceções, como no caso das nozes. A interseção das duas linhas representa a força de pré-carga na ligação sem uma carga externa aplicada. O ponto final da linha do parafuso é a força resistente máxima na rosca.

Além da linha dos parafusos e dos componentes, existe ainda uma outra linha característica importante da força de tração externa (também pré-carga). Esta linha é apresentada a cinzento na Figura 01. Esta origina-se na linha característica dos componentes no eixo y da força de aperto residual desejada. A força de aperto residual é a força que ainda mantém os componentes unidos. Por exemplo, se existe uma força horizontal a ser absorvida pela ligação (sem deformação de corte do parafuso, portanto, apenas pelo componente de atrito) além do componente de tração no caso da carga de trabalho existente, então a força de aperto residual tem de ser seleccionada de forma a existir uma resistência suficiente.

Além dessas linhas características, existem outras linhas que podem ser utilizadas para uma representação mais detalhada. No entanto, uma vez que essas linhas não têm influência no procedimento básico, não serão explicadas neste artigo, sendo apenas utilizado o diagrama de ligação simplificado apresentado. Por exemplo, as linhas características adicionais seriam devido ao conjunto de compressão ou à tensão e carga excêntricas.

Fórmulas de diagramas de ligações simplificados

Para criar um diagrama de ligação, é necessário calcular primeiro as rigidezes, deformações e forças correspondentes. Geralmente, a rigidez da mola pode ser calculada de acordo com a lei de Hooke da seguinte forma:

Onde,
c é a rigidez (constante de mola),
F é a força de mola,
f é a deformação (deflexão).

No caso de uma barra de tração com material isotrópico, a constante da mola pode ser calculada diretamente através do módulo de elasticidade (módulo de elasticidade):

Onde,
E é o módulo elástico,
A é a área da secção do tirante
l comprimento da barra de tração.

A rigidez do parafuso é simplificada e apenas é aplicada a secção do parafuso. Outras opções são aplicar a cabeça do parafuso, a rosca, a porca, diferentes diâmetros do eixo etc. Neste caso, os elementos com os seus valores recíprocos são adicionados à rigidez total. A rigidez da mola do parafuso é calculada através da seguinte fórmula (Índice S):

Onde,
c_S é a rigidez da mola do parafuso
E_S é o módulo de elasticidade do parafuso
A_S é a área da secção do parafuso
l_K é o comprimento de aperto (altura/espessura dos componentes).

O diâmetro do chanfro da rosca_d3 é utilizado para a área da secção no intervalo da rosca do parafuso. Assim, a fórmula total resulta:

A rigidez do componente é calculada de forma semelhante. Uma vez que existe uma chapa ou mais, é utilizado o índice P:

Onde,
c_P é a rigidez da mola dos componentes/placas,
E_P é o módulo elástico das placas,
A_P é a área da secção das placas
l_K é o comprimento de aperto (altura/espessura dos componentes).

A área da secção A_P depende da espessura, em contraste com o parafuso. É assumido que a carga é prolongada num ângulo de aproximadamente 60º. Existem três casos diferentes, como apresentado na Figura 02.

No caso 1, os componentes entre o parafuso e a porca são como uma manga e o diâmetro da manga é igual ao máximo do diâmetro da superfície de apoio do parafuso ou da porca.
O caso 2 cobre a gama onde este diâmetro da manga é no mínimo igual ao diâmetro da superfície de apoio da porca ou parafuso e no máximo igual ao diâmetro do cone de extensão de carga (marcado a vermelho na Figura 02). Esta estende-se simetricamente em ambos os lados e o diâmetro é maior no meio do comprimento de aperto.
O caso 3 cobre o intervalo desde o cone de extensão da carga máxima até à extensão infinita da placa. Por este motivo, é necessário calcular a área de substituição A_es. A_ers corresponde à área da secção de um cilindro de substituição com uma extensão de carga constante.

Para o exemplo a seguir, o Caso 3 é suficiente. O A_ers é calculado através da seguinte fórmula (ver VDI 2230, edição 1986 [1] ):

Onde,
d_W é o diâmetro da superfície de apoio,
d_h é o diâmetro do furo.

O diâmetro da superfície de apoio pode ser aplicado de forma simplificada como 90% da largura através dos planos:
d_W = 0,9 ∙ s (3,3)
Onde,
s é a largura nas superfícies planas da cabeça do parafuso/porca.

Uma vez que o ponto de aplicação da carga num modelo de superfície não se encontra necessariamente na parte superior do componente (a laje), mas sim sempre no meio da superfície, a rigidez da placa tem de ser determinada neste ponto de aplicação da carga. Para isso, é introduzido o fator de aplicação da carga n, o qual reduz o comprimento de aperto em conformidade. Este problema é ilustrado na Figura 03.

Os componentes reais (duas placas, neste caso) são reduzidos ao meio das superfícies. No caso de duas chapas, n é sempre 0,5, visto que é sempre utilizada metade de cada chapa. A nova rigidez da placa c_Pn é então calculada da seguinte forma:

Onde,
Φ_K é a relação de carga.

Para criar as linhas características, são ainda necessárias várias forças, além da rigidez. A carga de aperto residual F_KR, a carga de trabalho F_A, e o fator de aperto α_A (aperto de ângulo controlado) tem de ser especificados. As forças de montagem mínima e máxima resultantes F_{Mín e F Mmáx,} em contraste, devem ser calculadas. Abaixo encontra-se a fórmula para as pré-cargas de montagem com um aperto de ângulo controlado:
F_{Mín = F Kmín+} F_PA (3.6)
F_Mmáx = α_A ∙ F_Mmín (3,7)
Onde,
α_A é o fator de aperto para o método de ângulo controlado,
F_Kmín é a força de aperto residual mínima necessária na ligação,
F_PA é a carga de placa adicional devido à carga de trabalho.

A carga de placa adicional F_PA é a força que resulta quando se aplica a carga de trabalho. É calculada de acordo com a fórmula:
F_PA = (1 - n ∙ Φ_K ) ∙ F_A (3,8)
Onde,
F_A é a carga de trabalho.

Na simplificação sem considerar os assentamentos, a força de pré-esforço F_V corresponde à força de pré-esforço mínima F_Mmin. Para considerar a linha de carga de trabalho, falta a força máxima do parafuso F_Smax que surge no parafuso quando relativa à carga de trabalho:
F_Smáx = F_Mmáx + F_SA (3,9)
Onde,
F_SA força adicional dos parafusos

A força adicional do parafuso F_SA é calculada novamente de forma semelhante à Fórmula 3.8:
F_SA = n ∙ Φ_K ∙ F_A (3,10)

A capacidade de carga máxima do parafuso (F_0,2 ) como última força em falta tem de ser determinada com base na área da secção do parafuso na rosca. Esta é calculada através da área do diâmetro da secção d_s, que resulta do valor médio do diâmetro do núcleo d_k (d₃ ) e do diâmetro do flanco d_fl (d₂ ):

Onde,
d₂ é o diâmetro do chanfro da rosca
d₃ é o diâmetro do núcleo da rosca,
f_ub resistência à tração do material do parafuso

Além das forças, as deformações devem ser determinadas com os valores correspondentes para que as linhas características possam ser introduzidas no diagrama da ligação. Para isso, é utilizada a Fórmula 1.1 convertida de acordo com f. Abaixo estão as fórmulas para as deformações f das respetivas forças F:

Isso resulta nos seguintes pontos/valores de linha para o diagrama de ligação:

Linha característica	Deformação	Força
Parafuso	0	0
	f0,2	F0,2
Laje	fSMmáx	fMmáx
	fSMmáx + fPMmáx ou fMmáx	0
Carga de trabalho	fSMmáx + fSA	FMmáx - FPA
	fSMmáx + fSA	FMmáx + FSA = FSmáx

Tabela 1 – Pontos/valores da linha para diagrama de ligação

Modelação de uma ligação de parafuso pré-esforçada no RFEM

O modelo deve ser uma boa combinação de precisão e exequibilidade. Portanto, a ligação será constituída por superfícies, barras e sólidos de contacto.

Foram especificados os seguintes parâmetros para o exemplo de cálculo:
F_A = 25 kN
_FK = 10 kN
E_S = E_P = 210 000 N/mm²
t₁ = t₂ = 10 mm
l_K = t₁ + t₂ = 20 mm
d_h = 10 mm
D_A > d_W + l_K
n = 0,5
α_A = 1,0

Parafuso:
M10 8,8
f_ub = 800 N/mm²
_d2 = 9,03 mm
_d3 = 8,16 mm
s = 17 mm

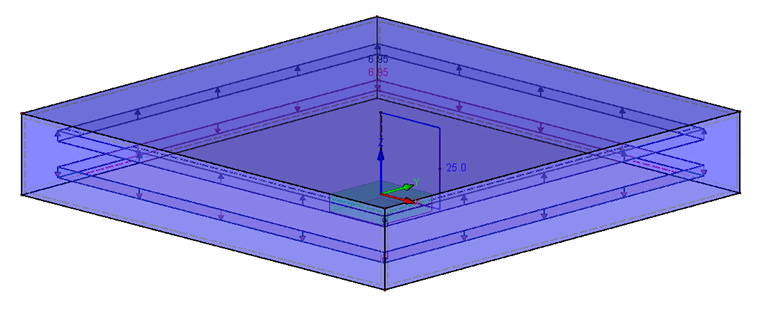
O modelo inclui duas superfícies quadradas sobrepostas com um orifício (diâmetro d_h ) no meio e que têm as dimensões 60 x 60 mm (para cumprir D_A > d_L + l_K ). Uma vez que t₁ = t₂, isto resulta num espaçamento de placas de 10 mm. A carga atua diretamente no meio da placa (fibra neutro). Assim sendo, o n resultante é 0,5. O modelo é suportado por um apoio fixo na extremidade inferior da barra de parafuso. Para obter uma força de apoio total igual a zero, a carga tem de ser aplicada tanto à chapa superior como à inferior. A carga é de 6,95 N/mm² para 25 kN da força total.

Para uma boa transferência de carga entre o parafuso (viga) e as placas, é modelada uma superfície rígida (anel) com o diâmetro exterior d_W em torno do furo. A ligação entre as chapas é gerada através de três sólidos de contacto. Um sólido está em volta do furo sem a parte da superfície rígida; dois sólidos de contacto apoiados em torno do buraco como duas cascas. Os sólidos de contacto têm de ser do mesmo material das placas para refletirem a rigidez entre as placas com precisão. Além disso, o contacto rompe ao ser ascendente e tem um atrito rígido na direção horizontal com um fator de 0,1.

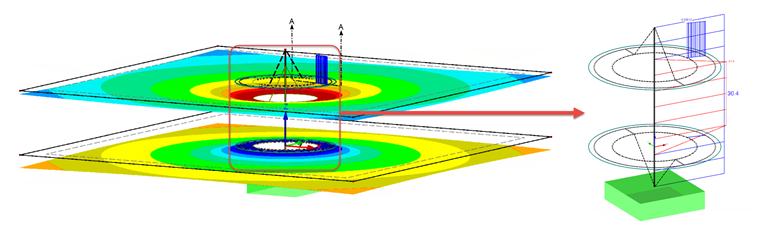
A estrutura é apresentada na Figura 04. O número 1 mostra as superfícies e barras com as dimensões reais. O número 2 mostra a superfície superior com a viga (parafuso) e as barras rígidas que representam a ligação entre o parafuso e a placa. A superfície rígida (cor-de-rosa) também tem uma barra rígida na borda interior para poder transferir quaisquer momentos.

Outro ponto importante é a malha de EF. Devido às pequenas dimensões, o tamanho principal da malha de EF para l_EF foi definido como 2 mm. Além do mais, o refinamento da malha de superfície foi definido com l_FE 0.2 mm nas superfícies rígidas.

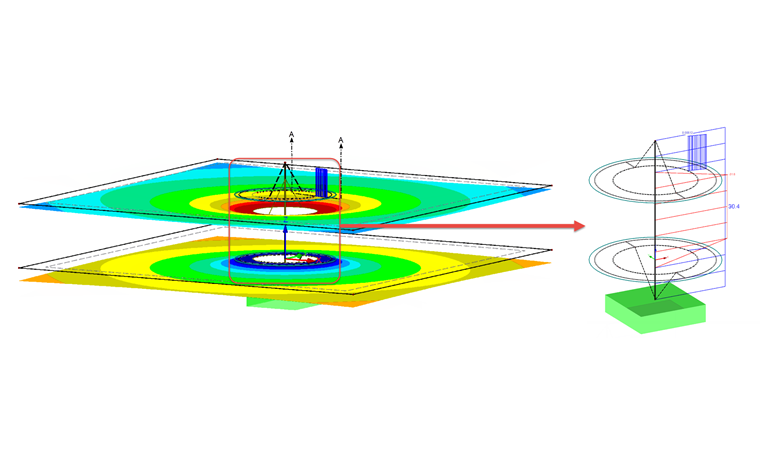
Uma vez que na prática nem o diâmetro do parafuso nem a força de trabalho sobre o parafuso são conhecidos, é possível modelar a estrutura sem a abertura e utilizar uma barra rígida em vez de uma viga para o primeiro dimensionamento do modelo e para a determinação das forças dos parafusos. Este modelo para pré-dimensionamento é apresentado na Figura 05.

Para poder detetar o pré-esforço residual no modelo, foi anexada uma barra resultante paralela ao parafuso (distância de 0,1 mm). Isso inclui todas as forças internas do sólido de contacto.

Comparação de soluções analíticas e numéricas

Para comparar as soluções, é necessário primeiro criar o diagrama da ligação. Os valores necessários estão listados na Tabela 1. Os valores intermédios e as linhas características apresentadas na Tabela 2 são obtidas através da substituição dos valores do exemplo prático (ver acima). A tabela 3 inclui o resumo dos valores mais importantes análogos à tabela 1 e a Figura 06 mostra o diagrama de ligação completo.

Símbolo	Número da fórmula	Valor
c[SCHOOL.NOTES]	2,2	549 kN/mm
Aers	3.2	303 mm²
cP	3,1	3182 kN/mm
ΦK	3,5	0,147
cPn	3,4	6921 kN/mm
FAT	3.10	1,8 kN
FAT	4.4	3 μm
fAP	3.8	23,2 kN
fMmáx	3.6, 3.7	33,2 kN
fSMmáx	4.2	60 μm
FMmáx	4.3	65 μm
F0,2	3,11	46,2 kN
f0,2	4.1	84 μm

Tabela 2 – Resultados intermédios e resultados de um exemplo de cálculo

Linha característica	Deformação [μm]	Força [kN]
Parafuso	0	0,0
	84	46,2
Laje	60	33,2
	65	33,2
Carga de trabalho	63	10.0
	63	35,0

Tabela 3 – Pontos/valores da linha característica do exemplo de cálculo

Foram inicialmente criados dois casos de carga para a solução numérica. O primeiro caso de carga (CC1 Pré-esforço) inclui a carga da barra do pré-esforço e o segundo caso (CC2 Carga de trabalho) inclui a carga de trabalho. Além disso, foi gerada a combinação de carga dos dois casos de carga (fator 1,0) (CO1: CC1 + CC2). O cálculo é baseado na análise estática linear com 15 incrementos de carga ( melhor convergência no caso de sólidos de contacto com rotura ).

Para o pré-esforço, é possível aplicar à barra o tipo de carga de barra pré-esforço inicial ou pré-esforço final. A pré-carga atual é o pré-esforço final. Uma vez que a carga de pré-esforço final requer muito tempo de cálculo, é recomendada a utilização da carga de barra do pré-esforço inicial. No entanto, isso tem a desvantagem de esta carga não incluir a força de reação através das placas. Portanto, a força axial na barra é muito pequena após o cálculo, uma vez que uma parte pode ser reduzida pela deformação das placas. Esta diferença pode ser reduzida de duas formas. Por um lado, isto pode ser previsto através da deformação da placa e convertido numa força adicional F_Zus,v (prevista) de acordo com a seguinte fórmula:
F_Zus,v = f_PMmáx ∙ c_S (5.1)

Por outro lado, isto também pode ser determinado iterativamente. Para isso, o caso de carga de pré-esforço deve ser calculado. A diferença entre o pré-esforço inicial aplicado e a força axial resultante na barra corresponde à força adicional F_Zus,i (iterativo). Pode ser utilizada a seguinte fórmula:
F_Zus,i = F_Mmáx - N_S (5.2)
Onde,
N_S é a força axial na barra com pré-esforço inicial F_Mmáx.

A força adicional F_Zus,v resulta dos valores na Tabela 2 da seguinte forma:
F_Zus,v = f_PMáx ∙ c_S = (f_Mmáx - f_SMmáx ) ∙ c_S = 5 μm ∙ 549kN/mm = 2,8 kN

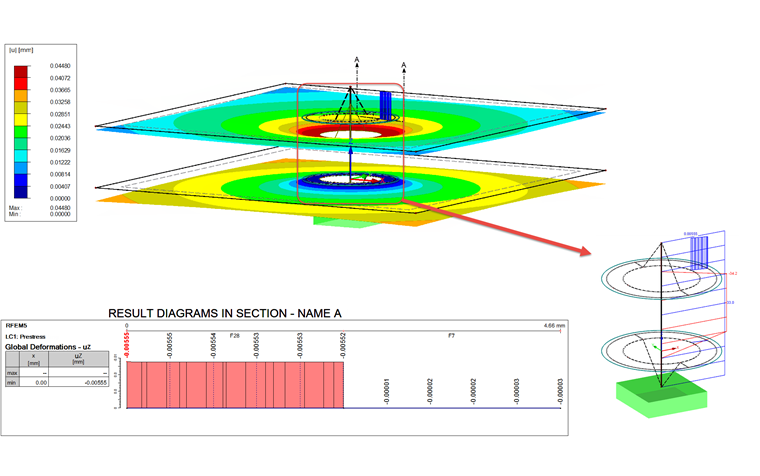
A força adicional iterativa F_Zus,i pode ser obtida após o cálculo do caso de carga na barra na Figura 07.

F_Zus,i = 33,2 kN - 30,4 kN = 2,8 kN

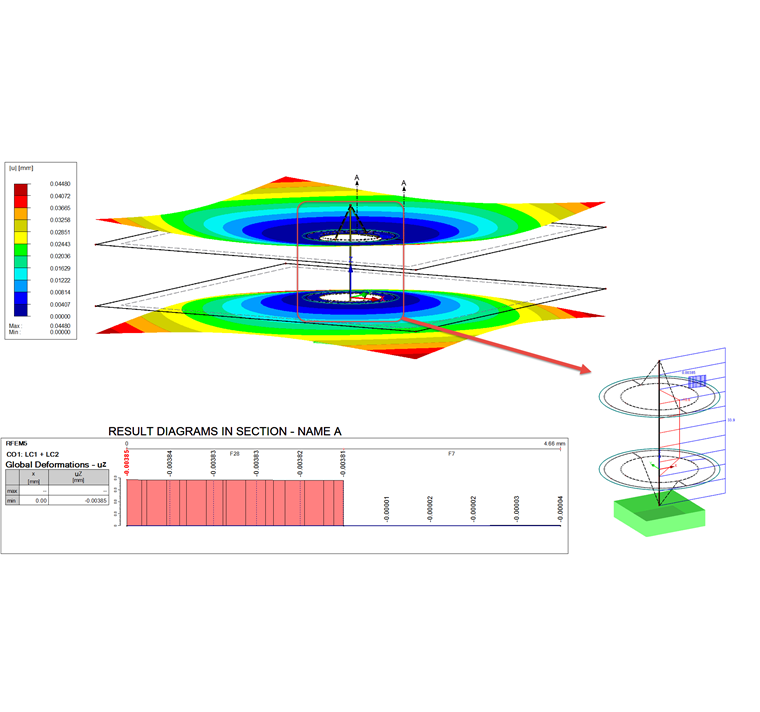
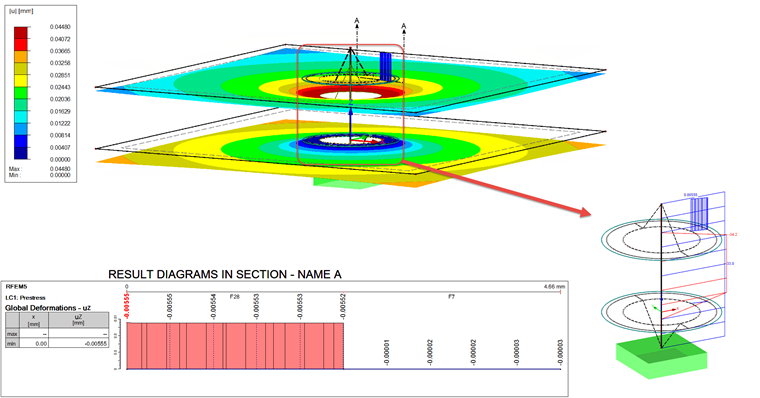
Assim, o pré-esforço resultante é de 36 kN em ambos os casos. Assim, é possível recalcular o caso de carga. O resultado é apresentado na Figura 08.

A barra de resultados adicional, que soma as forças de contacto de todos os sólidos de contacto, tem o resultado de 34,2 kN. Isto é cerca de 1,2 kN a mais do que a força axial da barra de parafuso que é de 33 kN. A deformação de ambas as superfícies (S1 e S27) apresentadas no diagrama deve ser adicionada de forma a poder compará-la com f_PMmax. Em média, isso resulta da seguinte forma:

A deformação é assim 0,6 μm maior do que a deformação calculada f_Mmáx.

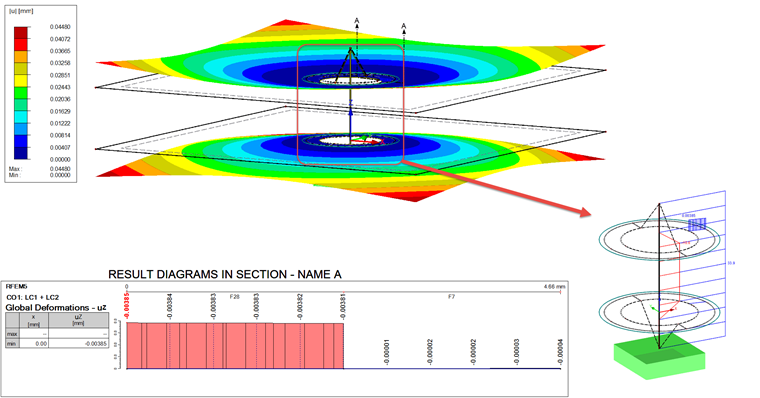
O resultado dos cálculos com carga de trabalho no CC1 é apresentado na Figura 09.

A barra de parafuso tem o resultado de 33,9 kN. Esta força de barra pode ser comparada com a força F_Smáx = 35 kN (ver Tabela 1 e Tabela 3, Carga de trabalho). A diferença é de 1,1 kN. O desvio das diferenças também é importante aqui. De acordo com o cálculo analítico, a diferença deveria ser igual à força F_SA = 1,8 kN. No entanto, a diferença com o modelo de EF é apenas metade, com 33,9 kN - 33 kN = 0,9 kN.

São obtidos desvios semelhantes no caso da deformação (ver diagrama na Figura 09). O valor apresentado é o valor reduzido pela carga de trabalho. Assim, a deformação tem de ser calculada pela carga de trabalho utilizando a deformação pelo pré-esforço. A deformação real é a diferença entre u_z,1 e a deformação média no diagrama. O valor de referência analítico é f_SA. Isto resulta na deformação u_z,2 :

Assim, a deformação é cerca de 1,4 μm menor do que a deformação calculada f_Mmáx.

Por fim, os resultados na barra de resultados são comparados. Como pode ver na Figura 09, a carga para a barra resultante é uma força de compressão de 10,6 kN. Este valor tem de ser comparado com a carga de aperto F_K = 10 kN. Isso resulta num desvio de 0,6 kN. A tabela 4 inclui um resumo dos resultados.

Símbolo	Analítico Valor	Cálculo pelo MEF		Desvio
		Barra	Laje
fMmáx [kN]	33,2	33,0	34,2	0,2/1,2
fPMmáx [μm]	5.0	-	5.6	0,6
fSA [μm]	3,0	-	1,6	1,4
FMmáx + FSA [kN]	35,0	33,9	-	1,1
FMmáx - FPA [kN]	10.0	-	10,6	0,6

Tabela 4 – Valores de comparação do modelo analítico/cálculo MEF

Avaliação

Como apresentado na Tabela 4, existem diferenças parcialmente grandes entre os modelos. Geralmente, as maiores correspondências encontram-se no caso de carga de Pré-esforço. Dependendo da avaliação da barra de resultados (placa) ou da barra de parafuso, os desvios em relação a F_Mmáx são de 3,6% ou 0,6% (em relação ao resultado analítico).

O maior desvio resulta da barra de parafuso e da deformação da placa após a aplicação da carga de trabalho. Neste caso, existe um desvio de 1,1 kN entre a força axial na barra e a solução analítica. Este desvio, em relação à solução analítica, é inicialmente de 3%. Contudo, a diferença é muito maior quando se refere à força adicional do parafuso. O desvio do modelo de MEF é o seguinte:
F_SA,FEM = (F_Mmáx + F_SA ) - F_Mmáx = 33,9 kN - 33 kN = 0,9 kN << 1,8 kN = F_SA

Estes desvios podem ser causados pelo facto de ambas as chapas não terem rigidez na direção z e o sólido de contacto ter apenas um elemento de EF na sua espessura. Assim, não pode haver extensão de carga dentro do sólido. A transferência de carga no sólido é realizada exclusivamente através da deformação da placa por flexão e força de corte. É óbvio a partir dos valores que o modelo de EF no caso de carga de Pré-esforço na combinação de placas e sólidos de contacto tem uma rigidez menor do que no modelo analítico (ver deformação menor). Neste momento, a rigidez mais alta do parafuso pode ser excluída, pois isso é determinado pela teoria da viga e pela secção.

Por outro lado, existe uma deformação menor no caso da combinação de cargas no modelo MEF ou a força do parafuso tem um incremento significativamente menor. Isto indica mais uma vez a maior rigidez da laje. Em resumo, existe apenas uma explicação para isso: A composição de uma placa e sólidos de contacto tem uma extensão de carga diferente, pelo que a abordagem da Fórmula 3.2 no modelo de MEF não é válida no formulário. Provavelmente, seria necessário examinar um exemplo real ou um modelo de MEF ampliado para descobrir qual é a solução mais próxima da realidade.

No entanto, é importante ter em atenção o seguinte: A força de aperto residual é quase idêntica nas duas variantes. Assim, o pré-esforço na ligação é bem modelado e pode ser utilizado para a análise da ligação.

Resumo

A modelação de uma ligação de parafuso pré-esforçada utilizando sólidos de contacto, superfícies e vigas é a combinação de uma solução prática e uma representação real. Prático significa que o tempo de cálculo é significativamente menor, em comparação com o cálculo com sólidos MEF, o que provavelmente representaria a ligação com mais precisão. No entanto, é necessário melhorar o dimensionamento dos parafusos ou realizar mais análises que relacionem os resultados com a realidade.

Uma vez que as forças de pré-carregamento e as forças de aperto residuais correspondem em grande parte às do cálculo analítico, pode assumir-se que este tipo de modelação pode ser utilizado para a análise da ligação.

Literatura

[1]	Associação de Engenheiros Alemão: (1986). Diretiva VDI 2230 – Cálculo sistemático de ligações aparafusadas com tensão elevada. Berlin: Beuth.