Система
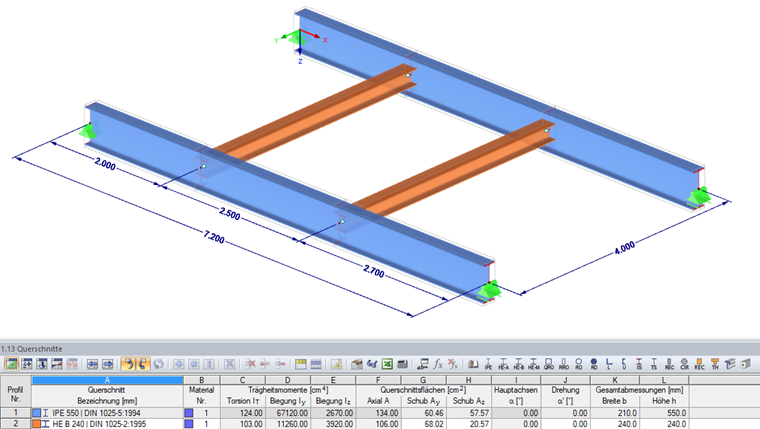
Профили:
Главные балки = IPE 550
Поперечные балки = HE-B 240
Материал:
Конструкционная сталь S235 по DIN EN 1993-1-1, таблица 3.1
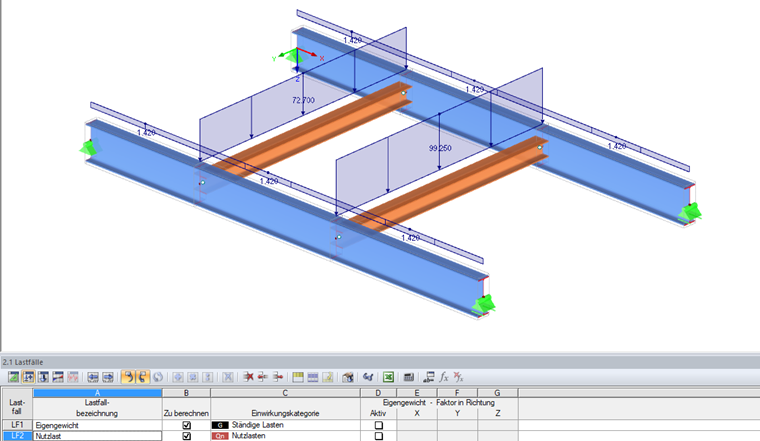
Расчетные нагрузки
LC 1 Собственный вес:
gd = 1,42 кН/м
LC 2 Полезная нагрузка:
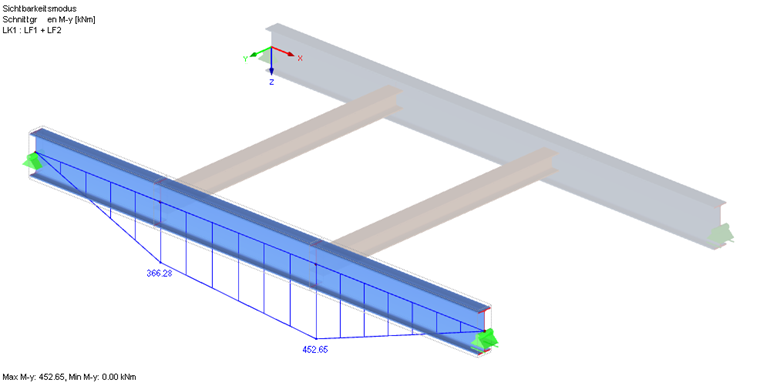
Расчетные внутренние силы
Расчет на устойчивость без учета поперечных балок согласно [3], пункт 6.3.2
Исходя из допущения, что в начале и конце стержня имеется поперечная фиксация и ограничение на кручение, в RF ‑ STEEL EC3 определяется идеальный критический момент для продольного изгиба при кручении Mcr , равный 368 кНм, в соответствии с проверкой в соответствии с [3 ] , П. 6.3.2. Таким образом, расчет по уравнению 6.54 дает 1,64. Следовательно, расчет по предельному состоянию по несущей способности нельзя выполнить без стабилизирующего эффекта поперечных балок.
Расчет на устойчивость с учетом поперечных балок по [3], приложение BB.2.2
Согласно DIN EN 1993-1-1, приложение BB.2.2 предполагается непрерывное защемление от поворота по длине балки. Поэтому имеющееся прерывное защемление от поворота «растягивается» до непрерывного защемления от поворота.
Определение непрерывного защемления от поворота:
Значения взяты из [2] и приведены в соответствие с обозначениями приложения BB.2.2.
Cθ,R,k = 11 823 кНм (составляющая от изгибной деформации поперечных балок)
Cθ,D,k = 359 кНм (составляющая деформации сечения главной балки, учитывается соединение со стенкой)
Преобразование в непрерывное ограничение вращения Cθ со средним расстоянием между второстепенными балками:
Определение требуемого защемления от поворота:
где
Kυ = 0,35 для коэффициента упругого использования сечения
Kθ = 10 по DIN EN 1993-1-1/NA, таблица BB.1
Возможно уменьшение Cθ,min на (MEd/Mel,Rd)²:
Расчет:
Cθ,prov = 134 кНм/м < Cθ,min = 200,9 кНм/м
Расчет посредством проверки достаточного защемления от боковой деформации главной балки по приложению BB.2.2 невозможно выполнить.
Расчет на устойчивость с учетом второстепенных балок в соответствии с [3] , п. 6.3.4
Определение имеющегося прерывного защемления от поворота:
Значения взяты из [2] и приведены в соответствие с обозначениями приложения BB.2.2.
Cθ,R,k = 11 823 кНм (составляющая от изгибной деформации поперечных балок)
Cθ,D,k = 359 кНм (составляющая деформации сечения главной балки, учитывается соединение со стенкой)
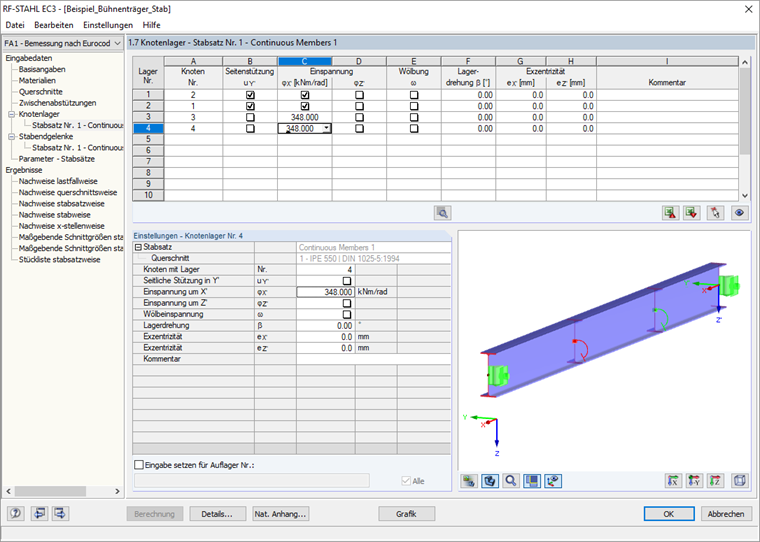
С помощью этой поворотной пружины можно описать конструктивную модель условно выделенного набора стержней для расчета в соответствии с п. 6.3.4 в окне 1.7 дополнительного модуля.
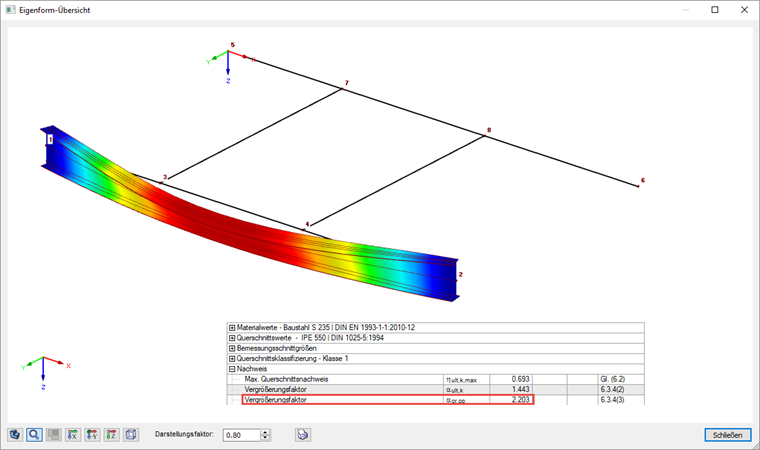
Во время проверки в соответствии с 6.3.4 резольвер для собственных значений, реализованный в RF ‑ STEEL EC3, определяет коэффициент αcr, op , с помощью которого может быть достигнута наименьшая идеальная критическая нагрузка потери устойчивости при деформациях из плоскости конструктивной системы.
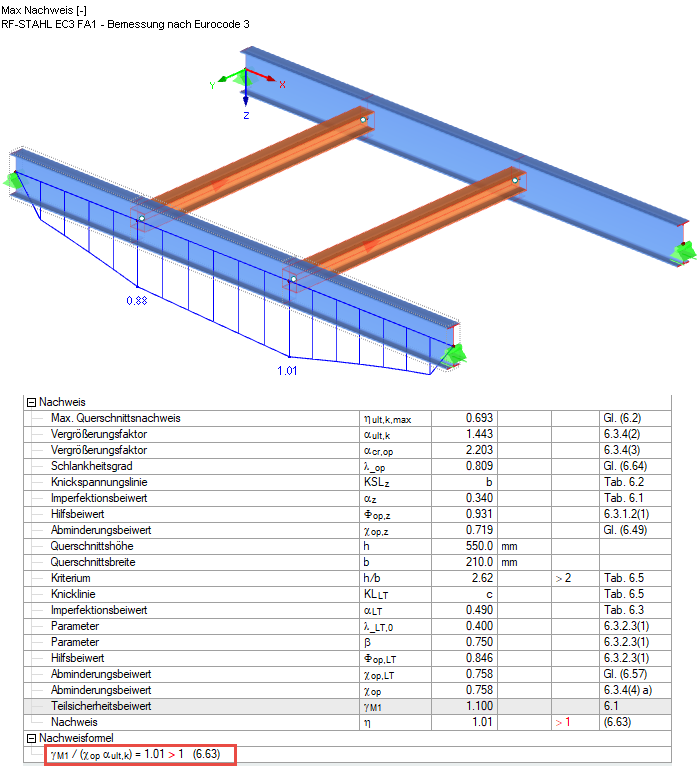
Критический коэффициент потери устойчивости показан среди промежуточных значений (см. Окна результатов), а соответствующая форма колебаний может быть отображена в отдельном окне. Таким образом, получается момент Mcr , равный 452,65 кНм ∙ 2,203 = 997,2 кНм.
Расчет по уравнению 6.63, таким образом, дает 1,01 для модели. Для расчета αcr, op точка приложения нагрузки была применена дестабилизирующим образом в соответствии с заданными параметрами на верхней полке. Учитывая, что реальная точка приложения нагрузки находится между верхней полкой и центром сдвига, можно не учитывать небольшое превышение и считать расчет выполненным.
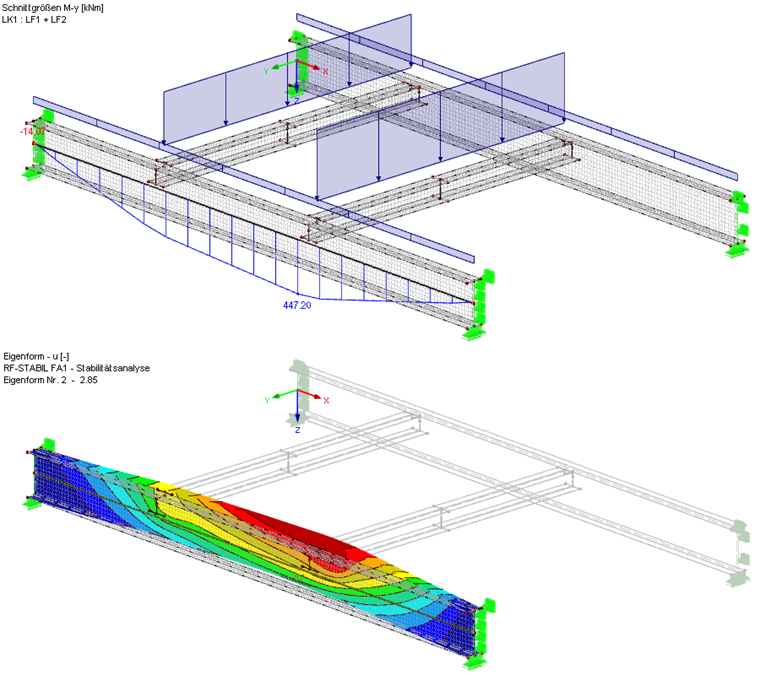
Определение Mкр на модели МКЭ
С помощью функции «Создать поверхности из стержня» и других доступных инструментов моделирования вы можете легко создать модель поверхности за минимальное время. С помощью типа стержня «Результирующая балка» можно определить и графически отобразить момент My в балке. Необходимый критический коэффициент потери устойчивости можно рассчитать для всей модели с помощью дополнительного модуля RF ‑ STABILITY.
С этой моделью МКЭ мы получаем момент Mcr , равный 447,20 кНм ∙ 2,85 = 1274,5 кНм. Это немного выше, чем результат для модели стержня с соответствующими дискретными пружинами вращения. Можно подумать о еще более точном моделировании соединений второстепенных балок.