Systém
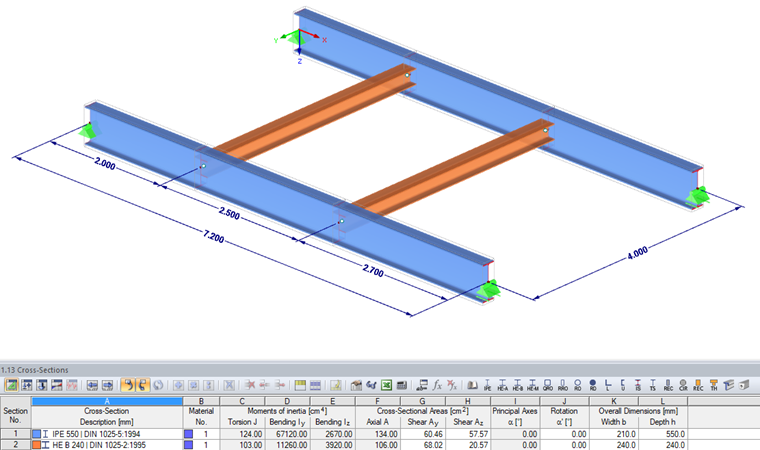
Průřezy:
Hlavní nosníky plošiny = IPE 550
Příčné nosníky = HE-B 240
Materiál:
Stavební ocel S235 podle EN 1993-1-1, tabulky 3.1
Návrhová zatížení
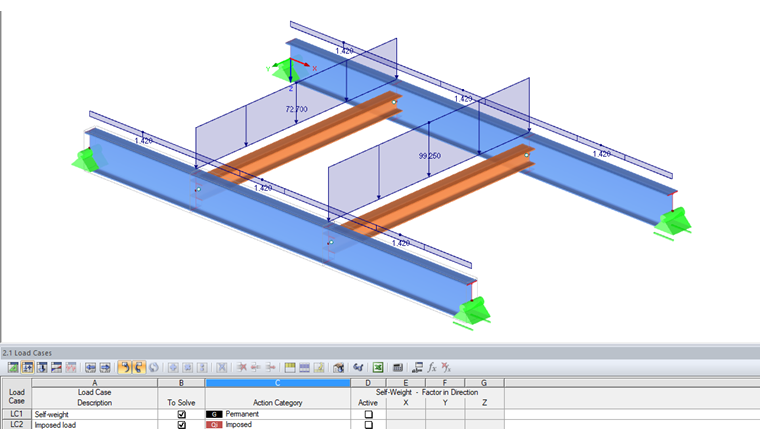
ZS 1 Vlastní tíha:
gd = 1,42 kN/m
ZS 2 Užitné zatížení:
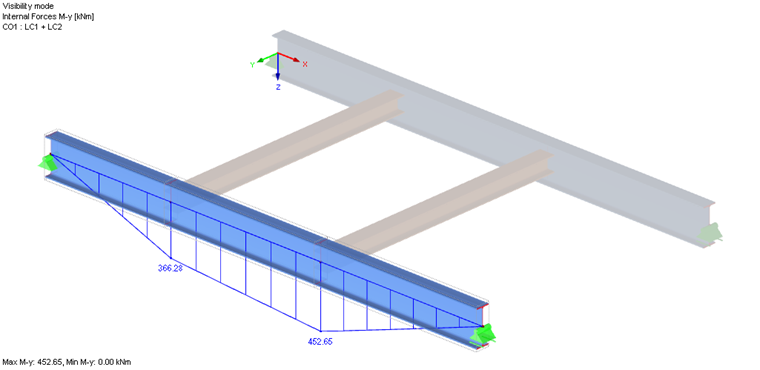
Návrhové vnitřní síly
Posouzení stability bez zohlednění příčných nosníků podle [3], čl. 6.3.2
Přídavný modul RF-STEEL EC3 vypočte v případě vidlicového uložení na začátku a na konci prutu v rámci posouzení podle [3], čl. 6.3.2 pružný kritický moment vzpěru Mcr 368 kNm. Výsledek posouzení podle rovnice 6.54 je tak 1,64. Únosnost tedy nemůže být prokázána bez stabilizačního účinku příčných nosníků.
Posouzení stability se zohledněním příčných nosníků podle [3], přílohy BB.2.2
Podle ČSN EN 1993-1-1, přílohy BB.2.2 se předpokládá spojité torzní uložení po délce nosníku. Nespojité torzní uložení se tedy „roztáhne“ ve spojité torzní uložení.
Stanovení spojitého torzního uložení:
Hodnoty se převezmou z [2] a upraví se pouze podle zápisu v příloze BB.2.2.
Cθ,R,k = 11 823 kNm (složka z deformace příčných nosníků ohybem)
Cθ,D,k = 359 kNm (složka z deformace průřezu hlavního nosníku, přípoj na stojinu se zohledňuje)
Přepočet na spojité torzní uložení Cθ se střední vzdáleností příčných nosníků:
Stanovení nutného torzního uložení:
kde
Kυ = 0,35 pro pružné využití průřezu
Kθ = 10 podle DIN EN 1993-1-1/NA, tabulky BB.1
Je možná redukce Cθ,min pomocí (MEd / Mel,Rd)²:
Posouzení:
Cθ,navrh = 134 kNm/m < Cθ,min = 200,9 kNm/m
Posouzení formou ověření dostatečného omezení boční deformace hlavního nosníku podle přílohy BB.2.2 nelze provést.
Stabilitní analýza se zohledněním příčných nosníků podle [3], čl. 6.3.4
Stanovení nespojitého torzního uložení:
Hodnoty se převezmou z [2] a upraví se pouze podle zápisu v příloze BB.2.2.
Cθ,R,k = 11 823 kNm (složka z deformace příčných nosníků ohybem)
Cθ,D,k = 359 kNm (složka z deformace průřezu hlavního nosníku, přípoj na stojinu se zohledňuje)
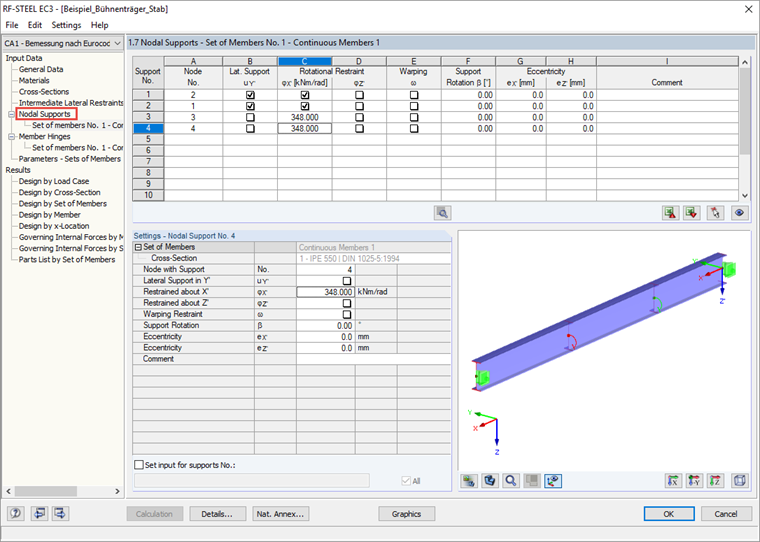
Pomocí této rotační pružiny lze pro posouzení podle článku 6.3.4 v dialogu 1.7 popsat statický model dané sady prutů.
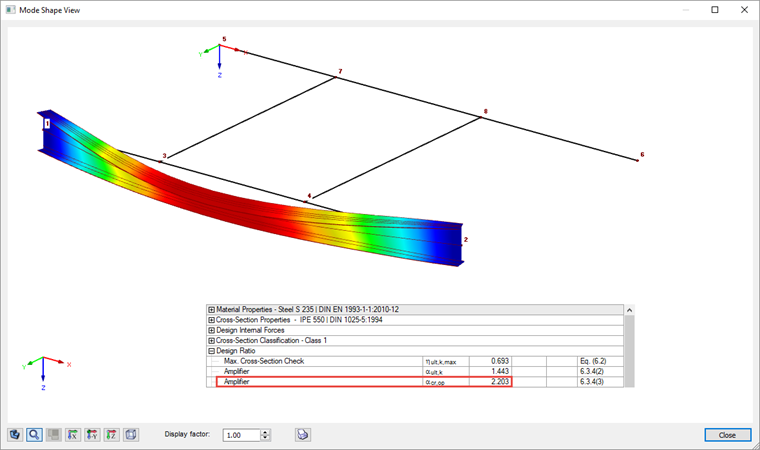
Při posouzení podle 6.3.4 se určí v modulu RF-STEEL EC3 řešením vlastních čísel součinitel αcr,op, kterým je dosaženo nejnižší pružné kritické zatížení s deformacemi z roviny konstrukce.
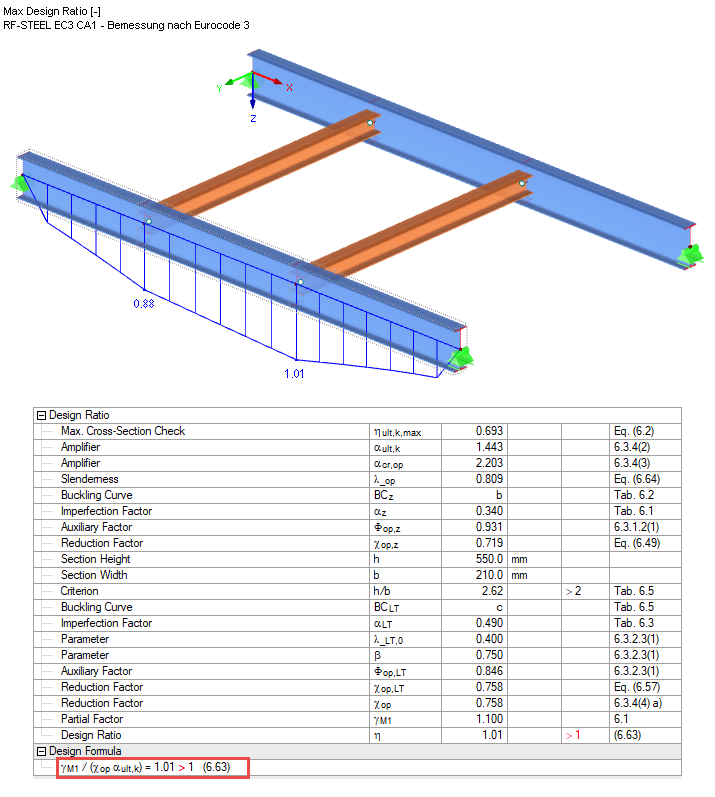
Součinitel kritického zatížení lze vyčíst v mezihodnotách (viz tabulky výsledků) a příslušný vlastní tvar lze zobrazit ve zvláštním okně. Výsledkem je moment Mcr 452,65 kNm ∙ 2,203 = 997,2 kNm.
Při posouzení podle rovnice 6.63 je tak využití u této konstrukce 1,01. Při výpočtu αcr,op se uvažovalo podle detailního nastavení destabilizující působiště zatížení na horní pásnici. Pokud zohledníme, že skutečné působiště zatížení leží mezi horní pásnicí a středem smyku, můžeme nepatrné překročení zanedbat a posouzení považovat za splněné.
Stanovení Mcr na MKP modelu
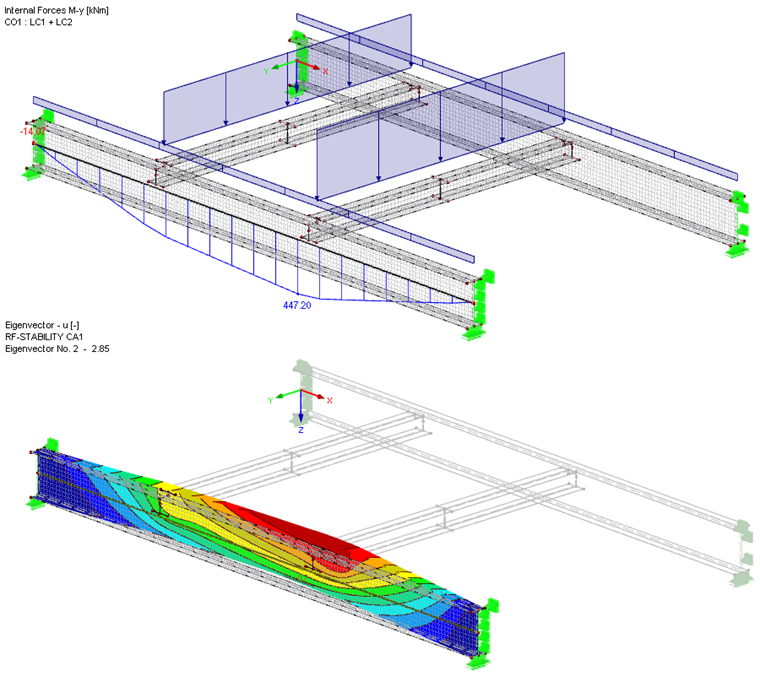
Pomocí funkce „Rozložit pruty na plochy“ a dalších nástrojů pro modelování lze pohodlně a s minimálními časovými nároky vytvořit plošný model konstrukce. Prut typu „Výsledkový prut“ umožňuje stanovit na nosníku moment My a graficky ho vyhodnotit. Potřebujeme pak už jen součinitel kritického zatížení, který lze vypočítat na celkovém modelu pomocí přídavného modulu RF-STABILITY.
Na MKP modelu dostaneme moment Mcr 447,20 kNm ∙ 2,85 = 1 274,5 kNm. To je o něco vyšší hodnota než výsledek na modelu prutu s odpovídajícími nespojitými rotačními pružinami. Můžeme pak zvážit ještě přesnější modelování přípojů příčných nosníků.