15560x

001512

2018-03-27

Lateral Torsional Buckling of Principal Beam with I-Section According to EN 1993-1-1

This example is described in technical literature [1] as Example 9.5 and in [2] as Example 8.5. A lateral-torsional buckling analysis must be performed for a principal beam. This beam is a uniform structural member. Therefore, the stability analysis can be carried out according to Clause 6.3.3 of DIN EN 1993-1-1. Due to the uniaxial bending, it would also be possible to perform the design using the General Method according to Clause 6.3.4. Additionally, the determination of the moment M_cr is validated with an idealized member model in line with the method mentioned above, using an FEM model.

System

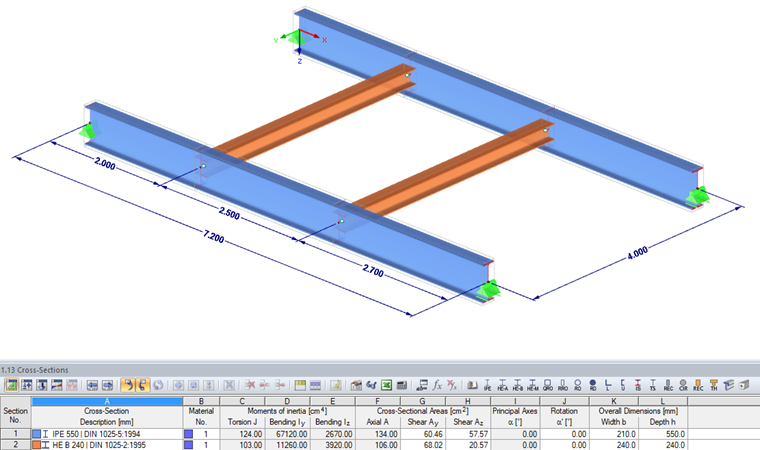
Cross-Sections:
Principal beams = IPE 550
Secondary beams = HE-B 240
Material:
Structural steel S235 according to DIN EN 1993‑1‑1, Table 3.1

Structural System

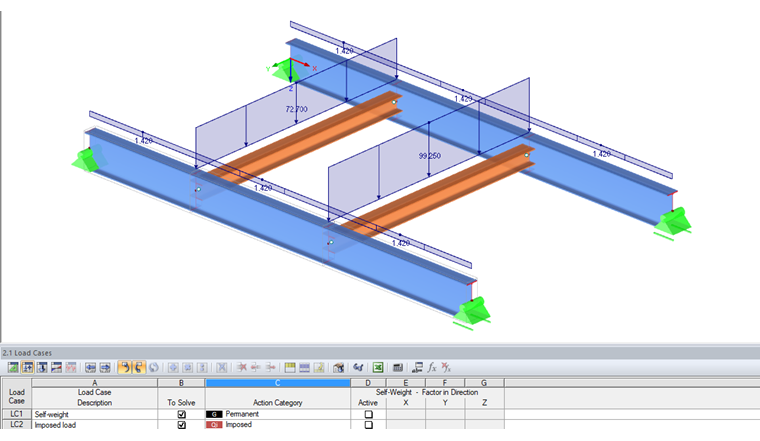
Design Loads

LC 1 Self-Weight:
g_d = 1.42 kN/m
LC 2 Imposed Load:

f_{1, d} = \frac{145.4 kN \cdot 2}{4 m} = 72.70 kN / m

Imposed Load of Secondary Beams

f_{2, d} = \frac{198.5 kN \cdot 2}{4 m} = 99.25 kN / m

Imposed Load of Principal Beams

Loads

Design Internal Forces

Distribution of Bending Moment My for Load Combination CO1 = LC1 + LC2

Stability Analysis Without Considering Secondary Beams According to [3] Clause 6.3.2

Under the assumption of a lateral and torsional restraint available at the member's start and end, an ideal critical moment for lateral torsional buckling M_cr of 368 kNm is determined in RF‑STEEL EC3 in line with the verification according to [3], Clause 6.3.2. Thus, the design according to Equation 6.54 results in 1.64. Hence, the ultimate limit state design cannot be fulfilled without the stabilizing effect of the secondary beams.

Stability Analysis Considering Secondary Beams According to [3], Annex BB.2.2

The rules of DIN EN 1993‑1‑1, Annex BB.2.2 assume a continuous rotational restraint over the beam's length. Therefore, the discrete rotational restraint available in the model is "smeared" to a continuous rotational restraint.

Determination of available continuous rotational restraint:
The values are taken from [2] and only adjusted to the notation of Annex BB.2.2.
C_θ,R,k = 11,823 kNm (a component due to the flexural deformation of the secondary beams)
C_θ,D,k = 359 kNm (a component due to the cross-section deformation of the principal beam, the connection to the web is considered)

Conversion to continuous rotational restraint Cθ with average distance of secondary beams:

x_{m} = \frac{2.5 m + 2.7 m}{2} = 2.6 m

Secondary Beams with Average Distance

C_{θ} = \frac{1}{(\frac{1}{11, 823} \frac{1}{359}) \cdot 2.6} = 134 kNm / m

Continuous Rotational Restraint

Determination of the required rotational restraint:

C_{θ, \min} = \frac{M_{pl, k}^{2}}{{EI}_{z}} \cdot K_{θ} \cdot K_{υ} = \frac{65, 330^{2}}{21, 000 \cdot 2, 670} \cdot 10 \cdot 0.35 = 266.4 kNm / m

Required Rotational Restraint

where
K_υ = 0.35 for the elastic cross-section ratio
K_θ = 10 according to DIN EN 1993‑1‑1/NA, Table BB.1

A reduction of Cθ,min by (MEd / Mel,Rd)² is possible:

C_{θ, \min} = 266.4 * {(\frac{452.7}{521.3})}^{2} = 200.9 kNm / m

Reduction of C_θ,min

Verification:
C_θ,prov = 134 kNm/m < C_θ,min = 200.9 kNm/m

The design in the form of the verification of a sufficient restraint for the principal beam's lateral deformation according to Annex BB.2.2 cannot be performed.

Stability Analysis Considering Secondary Beams According to [3], Clause 6.3.4

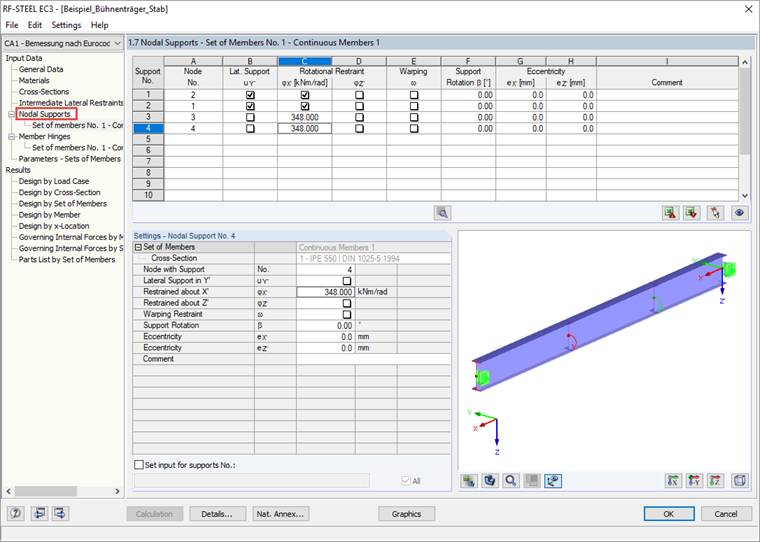
Determination of the available discrete rotational restraint:
The values are taken from [2] and only adjusted to the notation of Annex BB.2.2.
C_θ,R,k = 11,823 kNm (a component due to the flexural deformation of the secondary beams)
C_θ,D,k = 359 kNm (a component due to the cross-section deformation of the principal beam, the connection to the web is considered)

C_{θ} = \frac{1}{\frac{1}{11.823} \frac{1}{359}} = 348 kNm / rad

Discrete Rotational Restraint

With this rotational spring, it is possible to describe the structural model of the notionally singled out set of members for the design according to Clause 6.3.4 in Window 1.7 of the add-on module.

Rotational Spring in Window 1.7

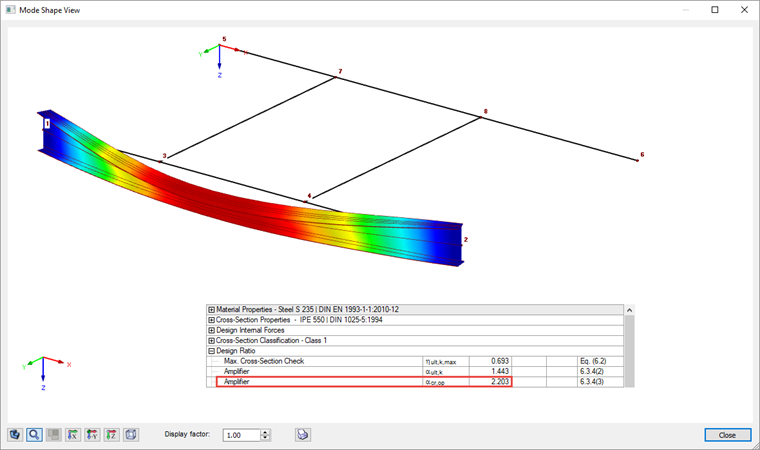
During the verification according to 6.3.4, a resolver for eigenvalues implemented in RF‑STEEL EC3 determines the factor α_cr,op, by which the smallest ideal critical buckling load can be reached with deformations from the structural system plane.

Factor αcr,op Determined by RF-STEEL EC3

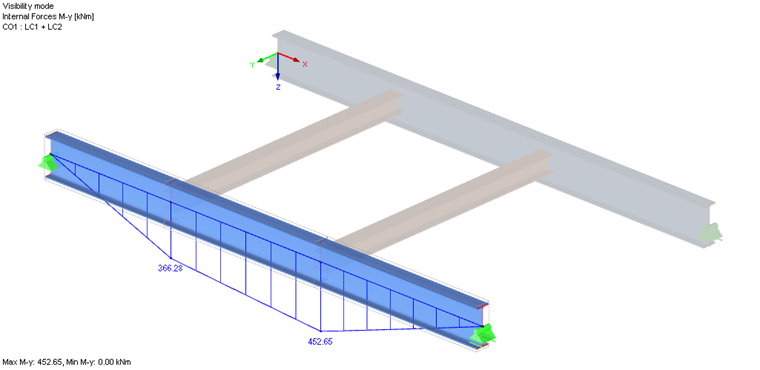
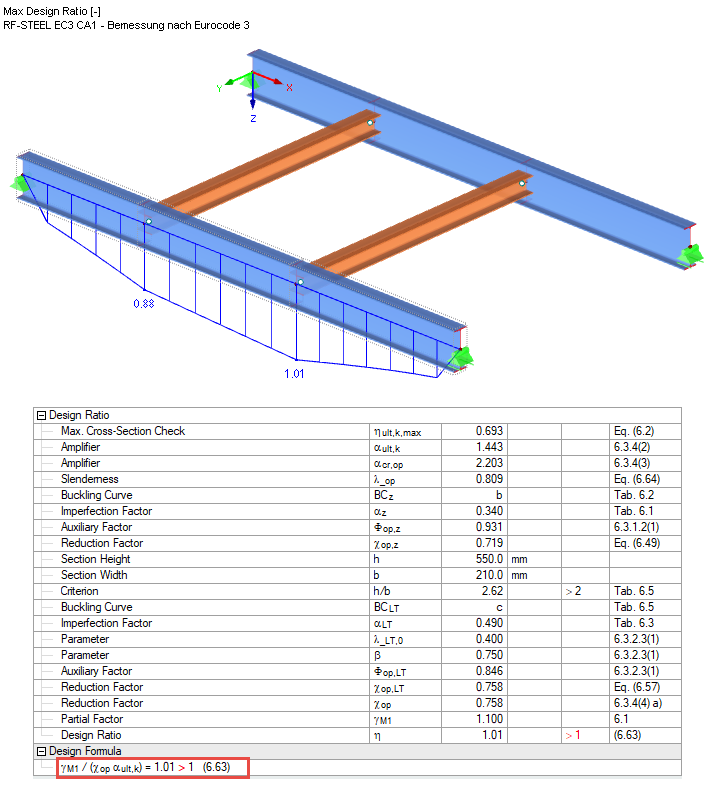
The critical buckling load factor is shown among the intermediate values (see the result windows) and the corresponding mode shape can be displayed in a separate window. Thus, the result is a moment M_cr of 452.65 kNm ∙ 2.203 = 997.2 kNm.

The design according to Equation 6.63 thus results in 1.01 for the model. For the calculation of α_cr,op the load application point was applied in accordance with the detail settings in a destabilizing way on the upper flange. Keeping in mind that the real point of load application is between the upper flange and the shear center, it is possible to ignore the slight exceedance and consider the design to be fulfilled.

Design in RF-STEEL EC3

Determination of M_cr on FEM Model

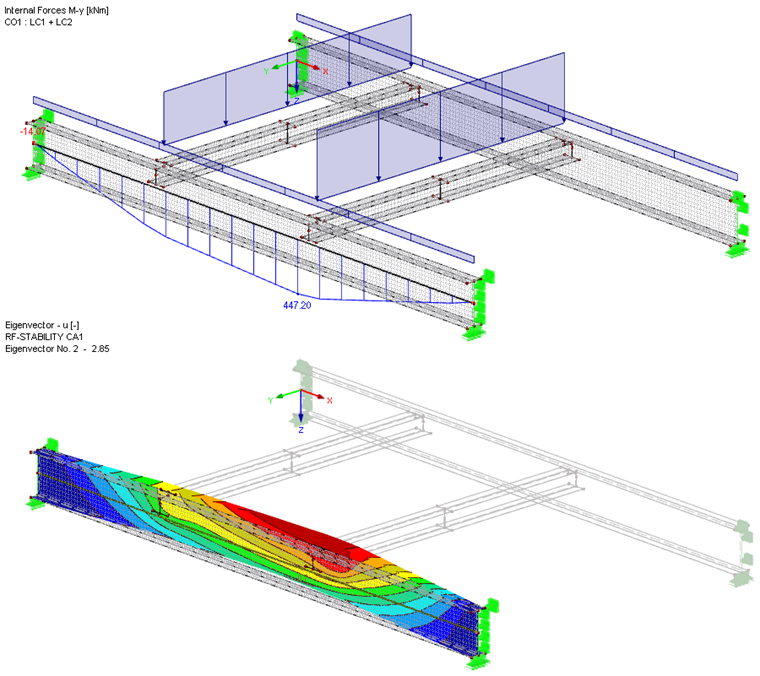
With the "Generate Surfaces from Member" function and other available modeling tools, you can easily create a surface model of the structure in a minimum amount of time. It is possible to determine and graphically display the moment M_y in the beam using the "Result Beam" member type. The critical buckling load factor that is needed can be calculated on the entire model with the RF‑STABILITY add-on module.

My in Beam (Above) and Critical Buckling Load Factor in RF-STABILITY (Below)

With this FEM model, we get a moment M_cr of 447.20 kNm ∙ 2.85 = 1,274.5 kNm. This is a bit higher than the result on the member model with corresponding discrete rotational springs. Consideration could be given to an even more accurate modeling of the connections of the secondary beams.

Links

Steel Structural Analysis & Design Software

References

Kuhlmann, U. (2013). Stahlbaukalender 2013. Berlin: Ernst & Sohn.
Lindner, J., Scheer, J., & Schmidt, H. (1994). Stahlbauten – Erläuterungen zu DIN 18800, Teil 1 bis Teil 4. Berlin: Ernst & Sohn.
European Committee for Standardization (CEN). (2010). Eurocode 3: Design of Steel Structures – Part 1‑1: General Rules and Rules for Buildings, EN 1993‑1‑1:2010‑12. Berlin: Beuth Verlag GmbH.
DIN Deutsches Institut für Normung e.V. (2015). National Annex – Nationally Determined Parameters – Eurocode 3: Design of steel structures – Part 1-1: General rules and rules for buildings; DIN EN 1993-1-1/NA:2015-08. Berlin: Beuth Verlag.
Dlubal Software. (2017). Training Manual EC3. Leipzig: Dlubal Software.