System
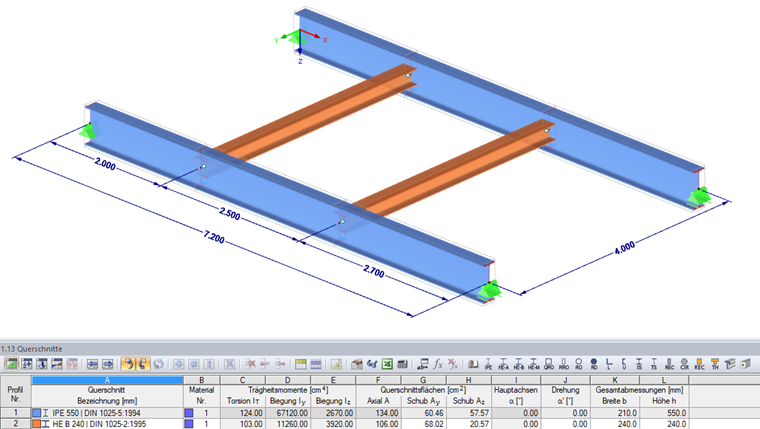
Profile:
Bühnenhauptträger = IPE 550
Querträger = HE-B 240
Material:
Baustahl S235 nach DIN EN 1993-1-1, Tabelle 3.1
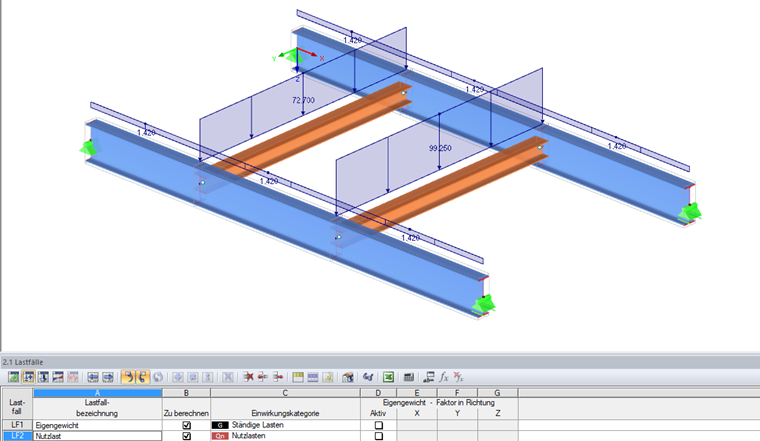
Bemessungslasten
LF 1 Eigengewicht:
gd = 1,42 kN/m
LF 2 Nutzlast:
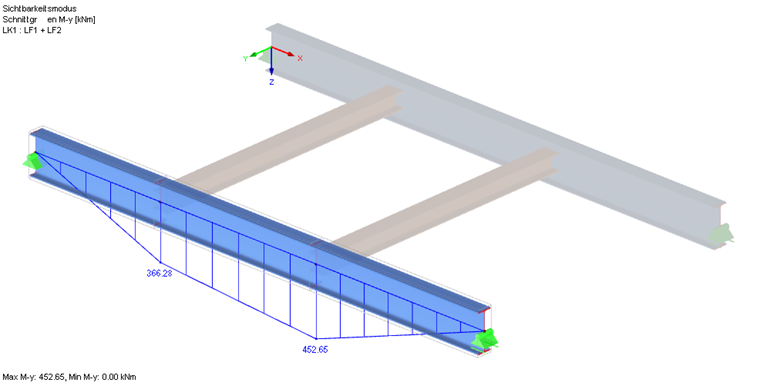
Bemessungsschnittgrößen
Stabilitätsnachweis ohne Berücksichtigung der Querträger nach [3] Abschnitt 6.3.2
Unter Annahme einer Gabellagerung am Stabanfang und -ende wird in RF-STAHL EC3 im Rahmen des Nachweises nach [3] Abschnitt 6.3.2 ein ideales Biegedrillknickmoment Mcr von 368 kNm ermittelt. Der Nachweis nach Gleichung 6.54 ergibt sich damit zu 1,64. Der Tragsicherheitsnachweis kann somit ohne den stabilisierenden Effekt der Querträger nicht erbracht werden.
Stabilitätsnachweis mit Berücksichtigung der Querträger nach [3] Anhang BB.2.2
Die Regelungen der DIN EN 1993-1-1 Anhang BB.2.2 setzen eine kontinuierliche Drehbettung über die Trägerlänge voraus. Die vorliegende diskrete Drehbettung wird daher in eine kontinuierliche Drehbettung "verschmiert".
Ermittlung der vorhandenen kontinuierlichen Drehbettung:
Die Werte werden aus [2] übernommen und lediglich an die Notation von Anhang BB.2.2 angepasst.
Cθ,R,k = 11.823 kNm (Anteil aus Biegeverformung der Querträger)
Cθ,D,k = 359 kNm (Anteil aus Profilverformung des Hauptträgers, Anschluss am Steg ist berücksichtigt)
Umrechnung in kontinuierliche Drehbettung Cθ mit mittlerem Abstand der Querträger:
Ermittlung der erforderlichen Drehbettung:
mit
Kυ = 0,35 für die elastische Querschnittsausnutzung
Kθ = 10 nach DIN EN 1993-1-1/NA, Tabelle BB.1
Es ist eine Abminderung von Cθ,min um (MEd / Mel,Rd)² möglich:
Nachweis:
Cθ,vorh = 134 kNm/m < Cθ,min = 200,9 kNm/m
Der Nachweis in Form des Nachweises einer ausreichenden Behinderung der seitlichen Verformung des Hauptträgers nach Anhang BB.2.2 kann nicht erbracht werden.
Stabilitätsnachweis mit Berücksichtigung der Querträger nach [3] Abschnitt 6.3.4
Ermittlung der vorhandenen diskreten Drehbettung:
Die Werte werden aus [2] übernommen und lediglich an die Notation von Anhang BB.2.2 angepasst.
Cθ,R,k = 11.823 kNm (Anteil aus Biegeverformung der Querträger)
Cθ,D,k = 359 kNm (Anteil aus Profilverformung des Hauptträgers, Anschluss am Steg ist berücksichtigt)
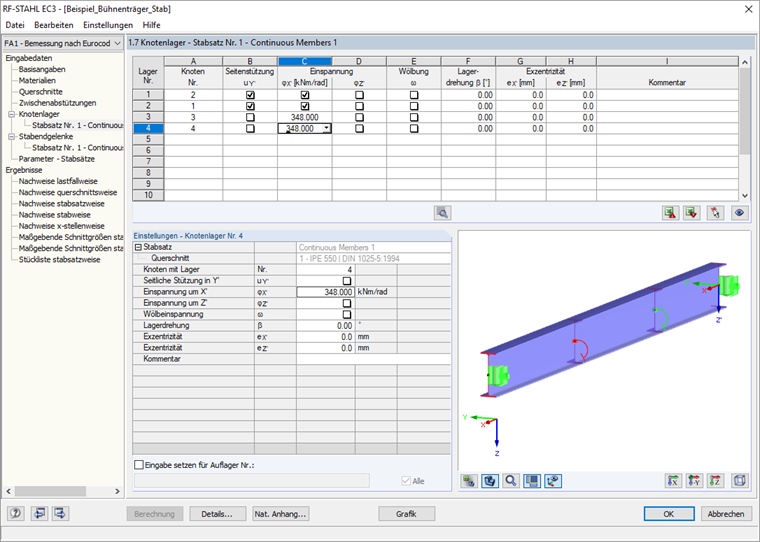
Mit dieser Drehfeder kann das statische Modell des herausgelösten Stabsatzes für den Nachweis nach Abschnitt 6.3.4 in der Maske 1.7 beschrieben werden.
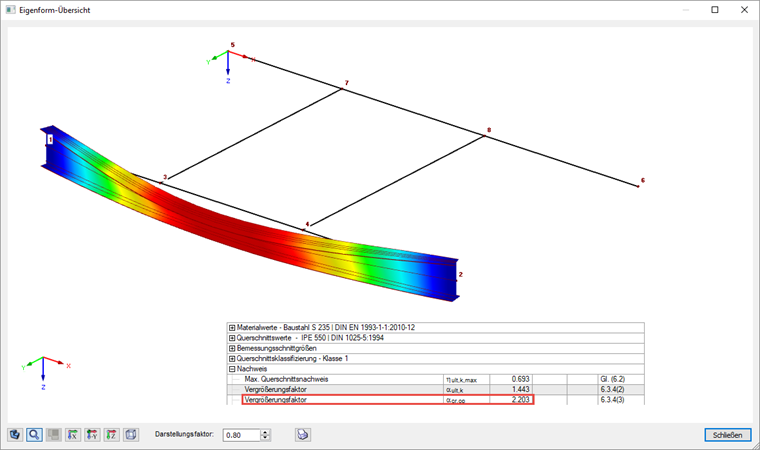
Beim Nachweis nach 6.3.4 ermittelt ein Eigenwertlöser in RF-STAHL EC3 den Faktor αcr,op, mit dem die kleinste ideale Verzweigungslast mit Verformungen aus der Tragwerksebene erreicht wird.
Den Verzweigungslastfaktor kann man in den Zwischenwerten (siehe Ergebnis-Masken) ablesen und die zugehörige Eigenform in einem separaten Fenster anzeigen. Es ergibt sich somit ein Mcr von 452,65 kNm ∙ 2,203 = 997,2 kNm.
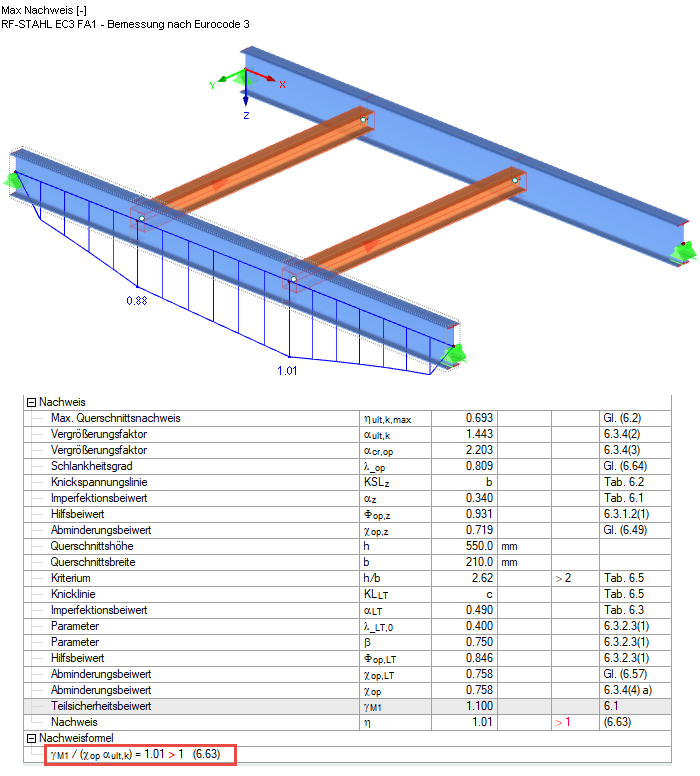
Der Nachweis nach Gleichung 6.63 ergibt sich für die Struktur damit zu 1,01. Für die Berechnung von αcr,op wurde der Lastangriffspunkt gemäß den Detaileinstellungen destabilisierend am Obergurt angesetzt. Unter Beachtung, dass der reale Lastangriffspunkt zwischen Obergurt und Schubmittelpunkt liegt, kann die geringfügige Überschreitung ignoriert und der Nachweis als erbracht betrachtet werden.
Ermittlung von Mcr am FEM-Modell
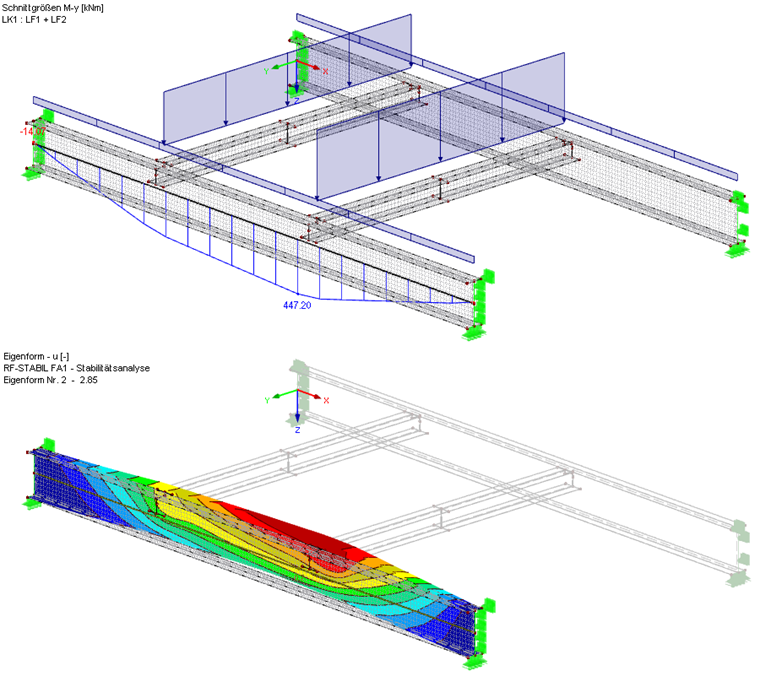
Mit der Funktion "Stab zerlegen in Flächen" und weiteren zur Verfügung stehenden Modellierungstools lässt sich ein Flächenmodell der Struktur komfortabel und mit minimalem Zeitaufwand erzeugen. Mit Hilfe des Stabtyps "Ergebnisstab" kann das Moment My im Träger ermittelt und grafisch ausgegeben werden. Der nun noch benötigte Verzweigungslastfaktor kann mit RF-STABIL am Gesamtmodell berechnet werden.
Es ergibt sich mit diesem FEM-Modell ein Mcr von 447,20 kNm ∙ 2,85 = 1.274,5 kNm. Dies liegt etwas höher als das Ergebnis am Stabmodell mit entsprechenden diskreten Drehfedern. Eine noch genauere Modellierung der Anschlüsse der Querträger könnte man in Erwägung ziehen.