System
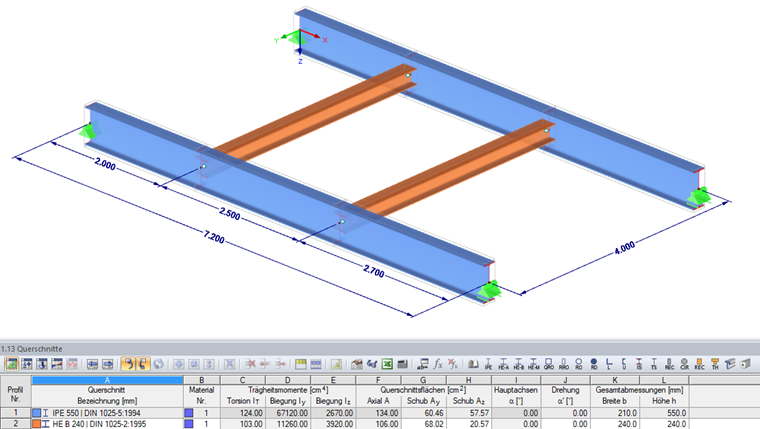
Przekroje:
Belki główne = IPE 550
Belki drugorzędne = HE-B 240
Materiał:
Stal konstrukcyjna S235 zgodnie z DIN EN 1993-1-1, Tabela 3.1
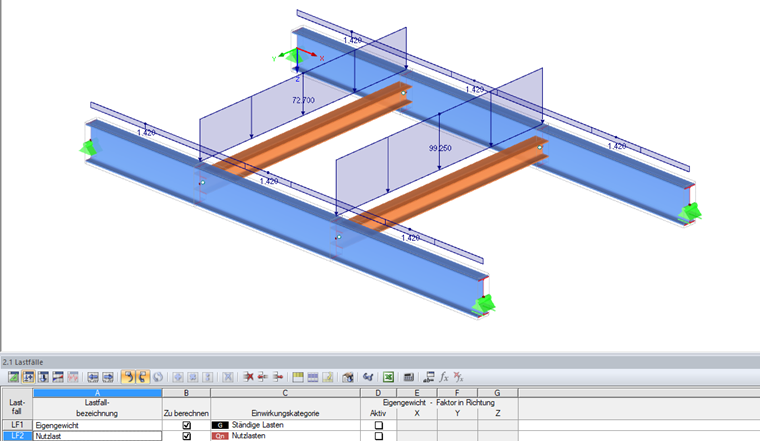
Obciążenia obliczeniowe
PO 1 Ciężar własny:
gd = 1,42 kN/m
PO 2 Obciążenie użytkowe:
Obliczeniowe siły wewnętrzne
Analiza stateczności bez uwzględnienia belek drugorzędnych zgodnie z [3] rozdz. 6.3.2
Przy założeniu, że istnieje utwierdzenie boczne i skrętne dostępne na początku i na końcu pręta, idealny moment krytyczny dla zwichrzenia Mcr wynoszący 368 kNm jest określany w RF-STEEL EC3 zgodnie z weryfikacją zgodnie z [3 ] , Punkt 6.3.2. W ten sposób wynik obliczeń zgodnie z równaniem 6.54 wynosi 1.64. Niezbędne jest zastosowanie stabilizacji za pomocą belek drugorzędnych aby spełnić warunki stanów granicznych.
Analiza stateczności z uwzględnieniem belek drugorzędnych zgodnie z [3], załącznik BB.2.2
Zasady zawarte w DIN EN 1993-1-1, załącznik BB.2.2 zakładają podporę na całej długości belki, która blokuje możliwość obrotu. Z tego względu dostępne w modelu dyskretne utwierdzenie obrotowe jest „rozmazane“ na ciągłe utwierdzenie obrotowe.
Określenie dostępnego ciągłego utwierdzenia obrotowego:
Wartości zaczerpnięto z [2] i dostosowano jedynie do zapisu załącznika BB.2.2.
Cθ,R,k = 11,823 kNm (część z odkształcenia na zginanie belek drugorzędnych)
Cθ,D,k = 359 kNm (uwzględnione połączenie ze środnikiem)
Konwersja na ciągłe ograniczenie obrotu Cθ przy średniej odległości belek drugorzędnych:
Określenie wymaganego utwierdzenia obrotowego:
Gdzie
Kυ = 0,35 dla stopnia wykorzystania przekroju sprężystego
Kθ = 10 zgodnie z DIN EN 1993-1-1/NA, tabela BB.1
Możliwa jest redukcja Cθ, min o (MEd/Mel, Rd )²:
Weryfikacja:
Cθ,prov = 134 kNm/m < Cθ,min = 200,9 kNm/m
Nie można przeprowadzić obliczeń w postaci sprawdzenia dostatecznego utwierdzenia bocznego odkształcenia głównej belki zgodnie z załącznikiem BB.2.2.
Analiza stateczności z uwzględnieniem belek drugorzędnych zgodnie z [3] , punkt 6.3.4
Określenie dostępnego dyskretnego utwierdzenia obrotowego:
Wartości zaczerpnięto z [2] i dostosowano jedynie do zapisu załącznika BB.2.2.
Cθ,R,k = 11,823 kNm (część z odkształcenia na zginanie belek drugorzędnych)
Cθ,D,k = 359 kNm (uwzględnione połączenie ze środnikiem)
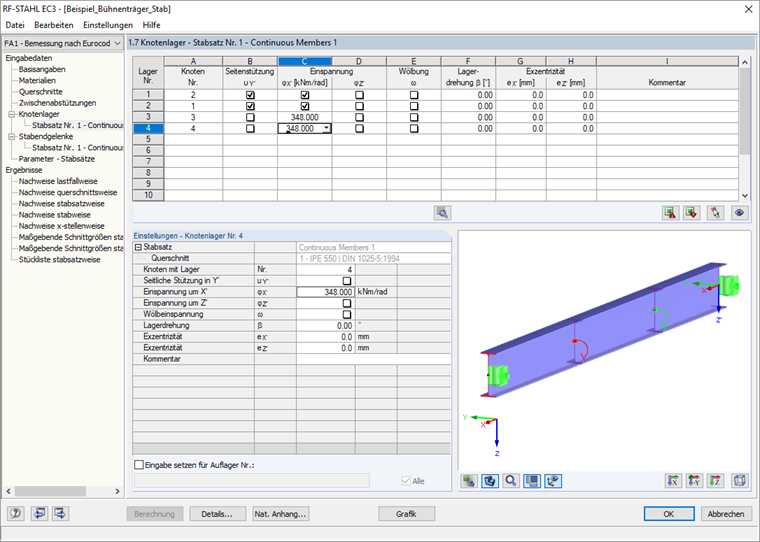
Dzięki zastosowaniu sprężyny obrotowej możliwe jest opisanie modelu konstrukcyjnego teoretycznie wyróżnionego zbioru prętów do obliczeń zgodnie z punktem 6.3.4 w oknie 1.7 modułu dodatkowego.
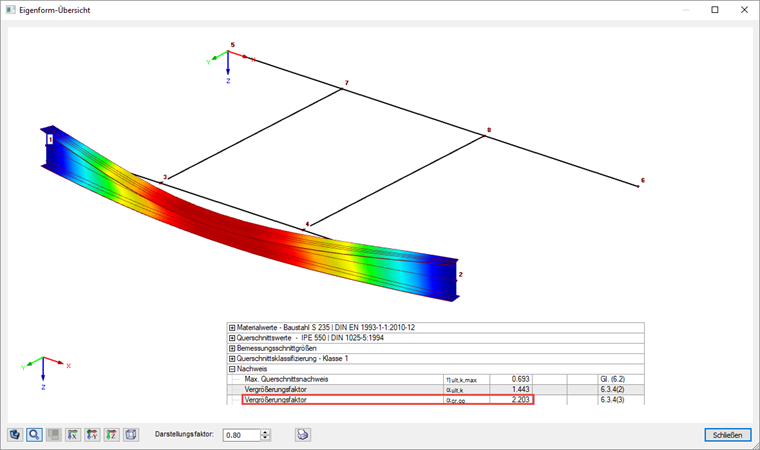
Podczas weryfikacji zgodnie z 6.3.4, solwer dla wartości własnych zaimplementowany w RF-STEEL EC3 określa współczynnik αcr,op , za pomocą którego można osiągnąć najmniejsze idealne obciążenie krytyczne wyboczeniowe wraz z odkształceniami od płaszczyzny konstrukcyjnej.
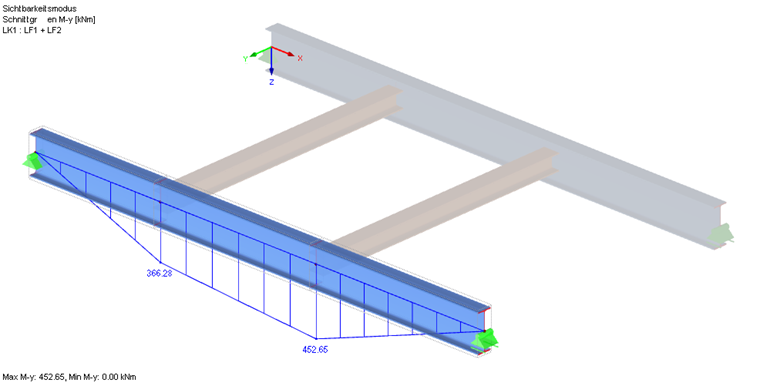
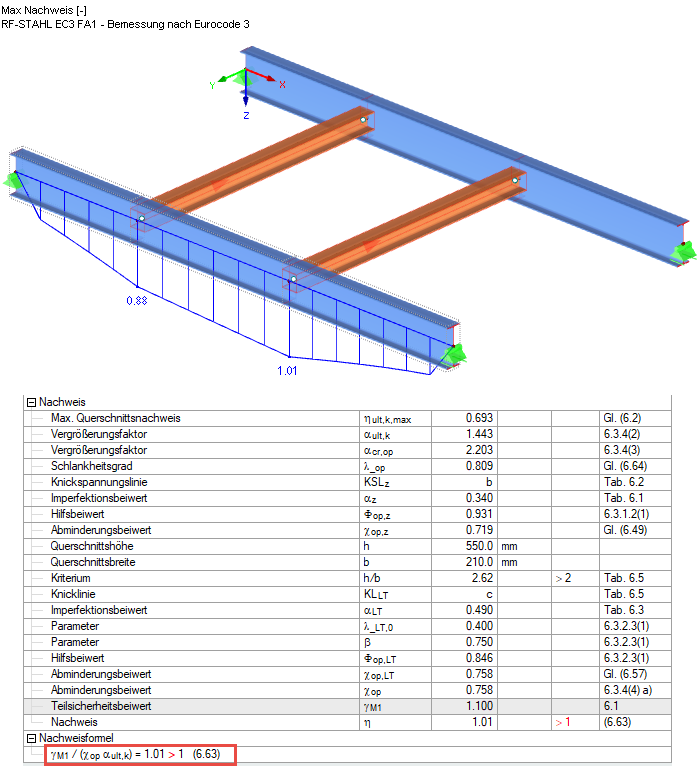
Współczynnik obciążenia krytycznego przy wyboczeniu jest wyświetlany wśród wartości pośrednich (patrz okna wyników), a odpowiedni kształt postaci może zostać wyświetlony w osobnym oknie. Zatem wynikiem jest moment Mcr 452,65 kNm ∙ 2,203 = 997,2 kNm.
Wynikiem obliczeń zgodnie z równaniem 6.63 jest zatem 1.01 dla modelu. Do obliczenia αcr,op punkt przyłożenia obciążenia został przyłożony zgodnie z ustawieniami w sposób destabilizujący na górnej półce. Mając na uwadze, że rzeczywisty punkt przyłożenia obciążenia znajduje się między górną półką a środkiem ścinania, można pominąć niewielkie przekroczenie i uznać, że obliczenia są spełnione.
Wyznaczanie Mcr na modelu MES
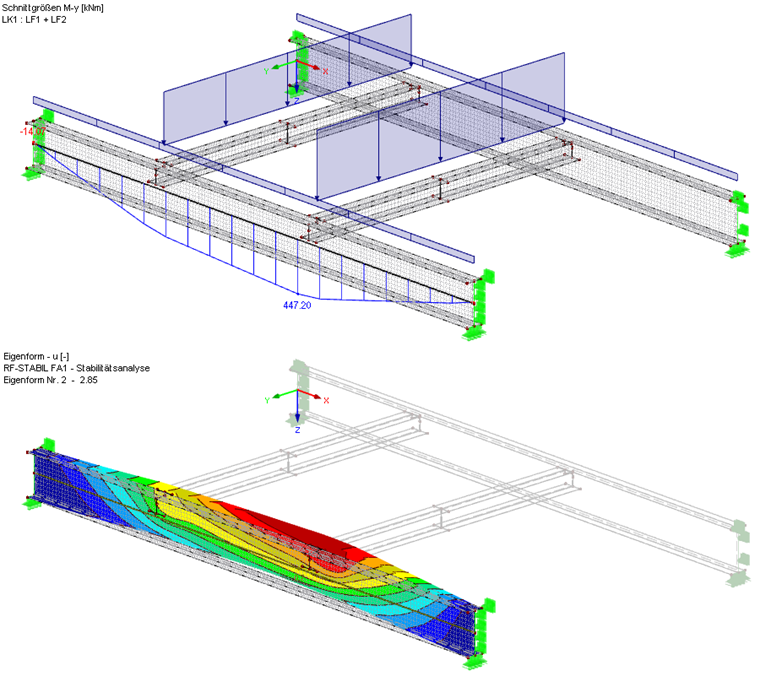
Dzięki funkcji "Generuj powierzchnie z pręta" i innym dostępnym narzędziom do modelowania można łatwo i szybko utworzyć model powierzchniowy konstrukcji. Przy użyciu typu pręta "Belka wynikowa" można określić i wyświetlić graficznie moment My w belce. Wymagany współczynnik obciążenia krytycznego przy wyboczeniu można obliczyć dla całego modelu za pomocą modułu dodatkowego RF-STABILITY.
W tym modelu MES otrzymujemy moment Mcr równy 447,20 kNm ∙ 2,85 = 1,274,5 kNm. Jest to nieco wyższy wynik niż wynik na modelu pręta z odpowiednimi dyskretnymi sprężynami obrotowymi. Można by rozważyć jeszcze dokładniejsze modelowanie połączeń belek podrzędnych.