Système
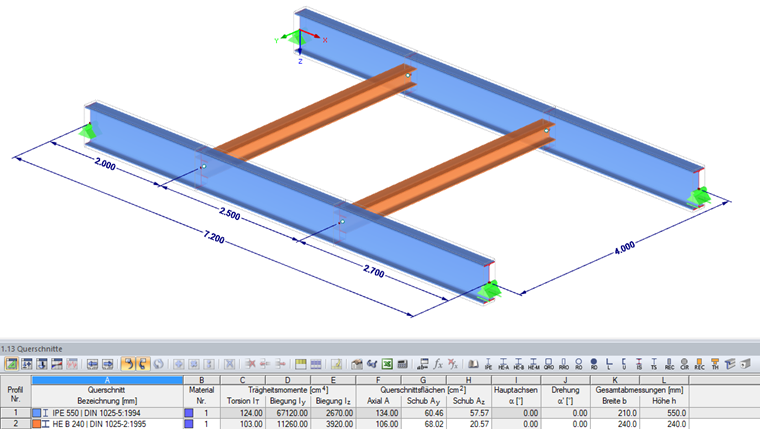
Sections :
Poutres principales = IPE 550
Poutres secondaires = HE-B 240
Matériau :
Acier de construction S235 selon la DIN EN 1993-1-1, tableau 3.1
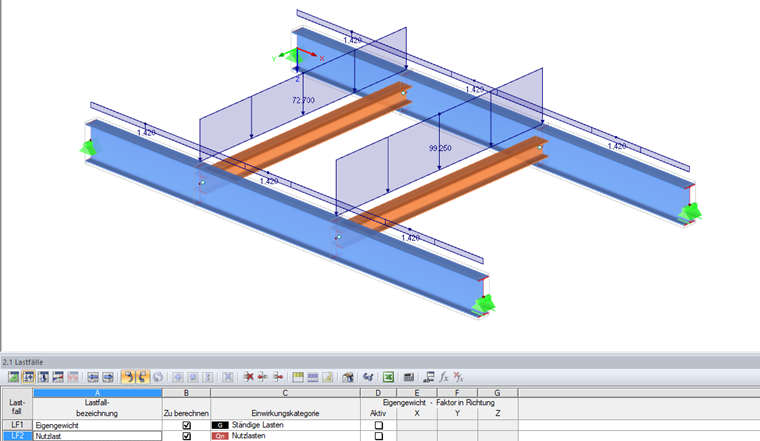
Charges de calcul
CC 1 Poids propre :
gd = 1,42 kN/m
CC 2 Charge imposée :
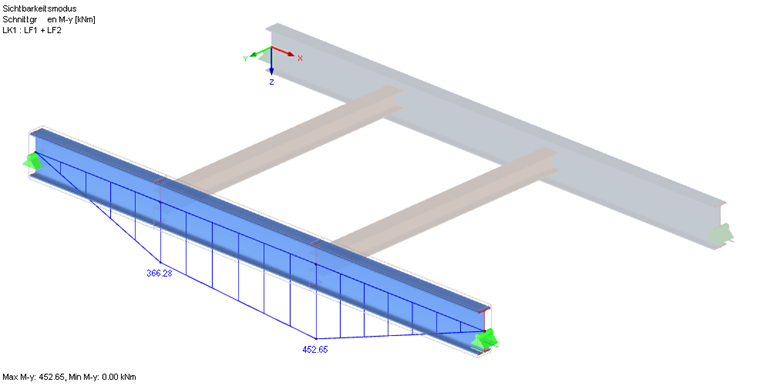
Efforts internes de calcul
Analyse de stabilité sans considérer les poutres secondaires selon [3] la partie 6.3.2
Dans l'hypothèse où un maintien latéral et un maintien en torsion sont disponibles au début et à la fin de la barre', un moment critique idéal pour le déversement Mcr de 368 kNm est déterminé dans RF-STEEL EC3 selon la vérification selon [3 ] , Article 6.3.2. Ainsi, le calcul selon l'Équation 6.54 donne 1,64. Par conséquent, la vérification à l'état limite ultime ne peut pas être satisfaite sans l'effet stabilisateur des poutres secondaires.
Analyse de stabilité en considérant les poutres secondaires selon [3], Annexe BB.2.2
Les règles de l'Annexe BB.2.2 de la norme DIN EN 1993-1-1 supposent des maintiens en rotation continus sur la longueur de la poutre. Par conséquent, les maintiens en rotation ponctuels disponibles dans le modèle sont « répartis » en maintiens en rotation continus.
Détermination des maintiens en rotation continus disponibles :
Les valeurs sont tirées de [2] et ajustées uniquement selon la notation de l'annexe BB.2.2.
Cθ,R,k = 11,823 kNm (un composant dû à la déformation en flexion des poutres secondaires)
Cθ,D,k = 359 kNm (un composant dû à la déformation de la section de la poutre principale, l'assemblage à l'âme étant considéré)
Conversion en maintien de rotation continu Cθ avec la distance moyenne des poutres secondaires :
Détermination des maintiens en rotation requis :
où
Ku = 0,35 pour le rapport de section élastique
Kθ = 10 selon la DIN EN 1993-1-1/NA, Tableau BB.1
Une réduction de Cθ, min par (MEd/Mel, Rd)² est possible :
Vérification :
Cθ,prov = 134 kNm/m < Cθ,min = 200.9 kNm/m
Il est impossible d'effectuer le calcul sous forme de vérification de maintiens suffisants pour la déformation latérale de la poutre principale selon l’Annexe BB.2.2.
Analyse de stabilité pour les poutres secondaires selon [3] , Clause 6.3.4
Détermination de maintiens en rotation ponctuels disponibles :
Les valeurs sont tirées de [2] et ajustées uniquement selon la notation de l'annexe BB.2.2.
Cθ,R,k = 11,823 kNm (un composant dû à la déformation en flexion des poutres secondaires)
Cθ,D,k = 359 kNm (un composant dû à la déformation de la section de la poutre principale, l'assemblage à l'âme étant considéré)
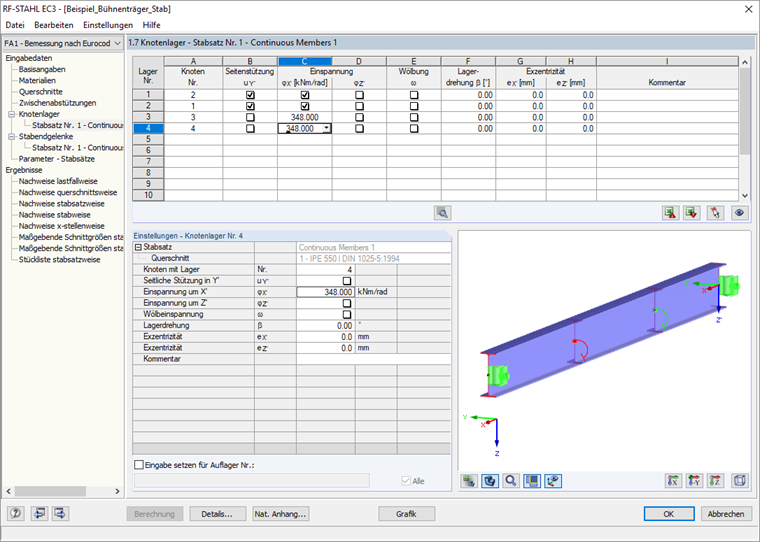
Ce ressort de rotation permet de décrire le modèle structurel de l’ensemble de barres exclu pour la vérification selon la Clause 6.3.4 dans la fenêtre de module 1.7.
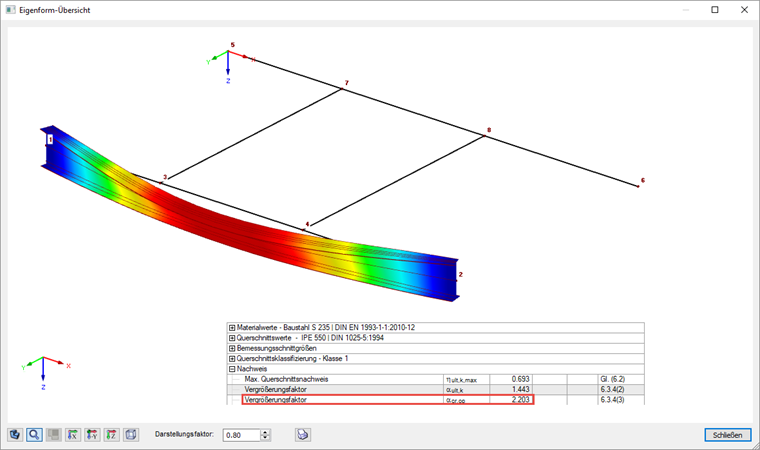
Lors de la vérification selon 6.3.4, un résolveur de valeurs propres implémenté dans RF-STEEL EC3 détermine le facteur αcr,op , grâce auquel la plus petite charge critique idéale de flambement peut être atteinte avec des déformations à partir du plan du système de structure.
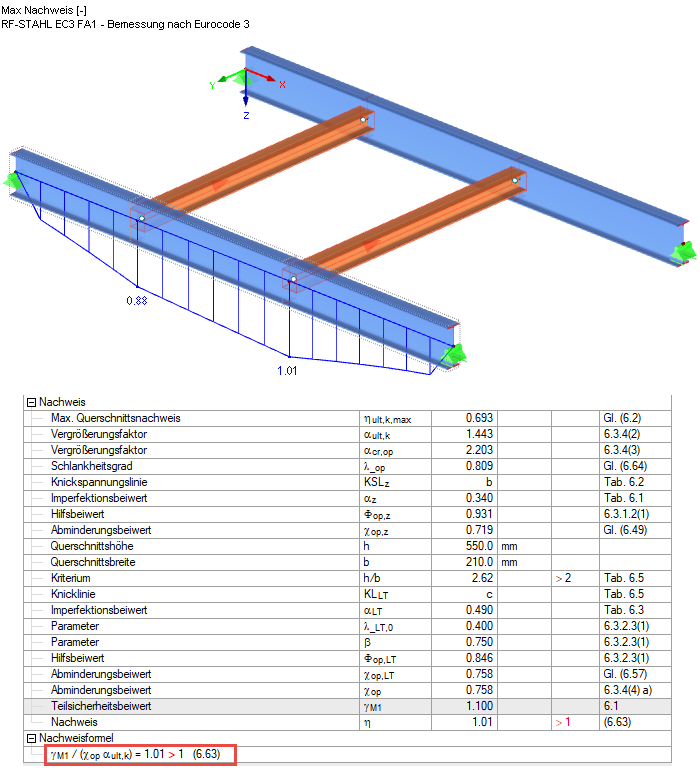
Le coefficient de charge critique de flambement est affiché parmi les valeurs intermédiaires (voir les fenêtres de résultat) et le mode propre correspondant peut être affiché dans une fenêtre à part. Le résultat est donc un moment Mcr de 452,65 kNm 2,203 = 997,2 kNm.
Par conséquent, le calcul selon l’équation 6.63 résulte pour le modèle d’un coefficient de 1,01. Pour le calcul decr,op, le point d'application de la charge a été appliqué de manière déstabilisante sur la semelle supérieure conformément aux paramètres de détail. En gardant à l’esprit que le vrai point d’application se situe entre la semelle supérieure et le centre de cisaillement, il est possible d’ignorer le léger dépassement et considérer le calcul comme complet.
Détermination de Mcr sur le modèle aux éléments finis
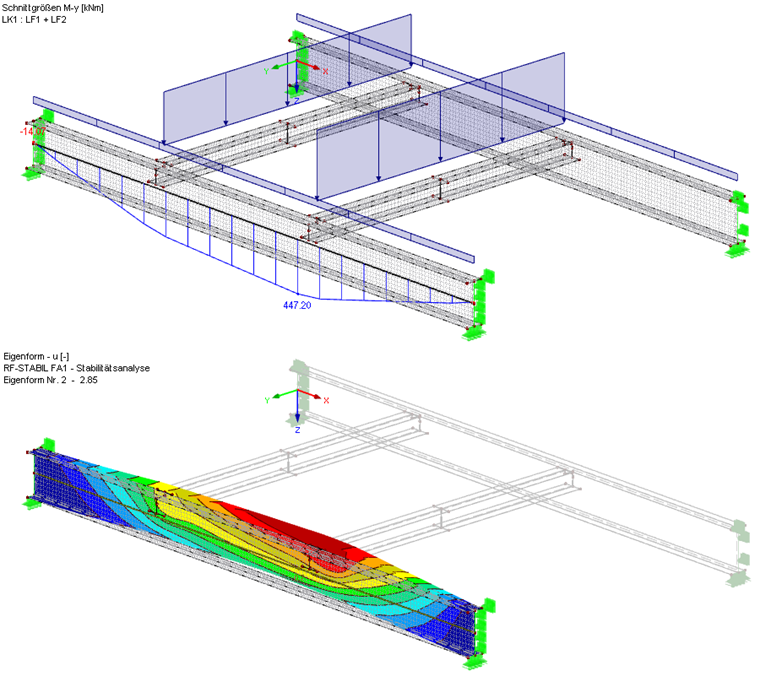
La fonctionnalité « Générer les surfaces à partir de la barre » et d’autres outils de modélisation permettent de créer facilement un modèle surfacique de la structure en très peu de temps. Il est possible de déterminer et d'afficher graphiquement le moment My dans la poutre à l'aide du type de barre « Poutre résultante ». Le coefficient de charge critique de flambement nécessaire peut être calculé sur le modèle entier avec le module RF-STABILITY.
Avec ce modèle aux éléments finis, nous obtenons un moment Mcr de 447,20 kNm 2,85 = 1 274,5 kNm. Ce résultat est légèrement plus élevé que celui sur le modèle de barre aux ressorts de rotation discrétisés correspondants. Une modélisation plus précise des fixations des poutres secondaires peut également être considérée.