系统
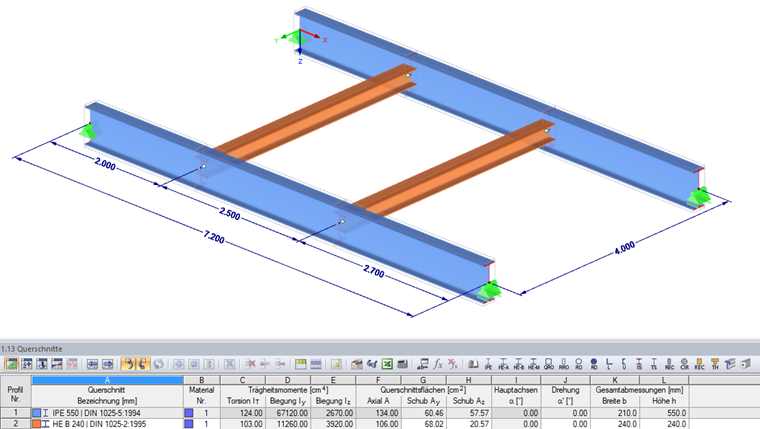
截面:
平台主梁 = IPE 550
次梁 = HE-B 240
材料:
钢材 S235 材料属性按照 DIN EN 1993-1-1, 表格 3.1
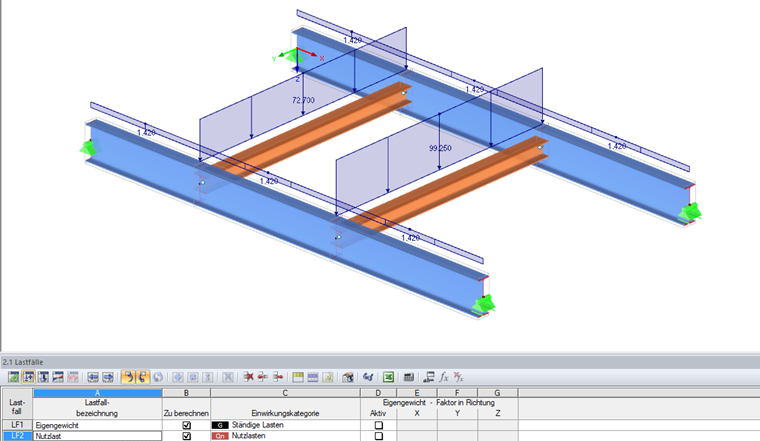
荷载设计值
LF 1 自重:
gd = 1.42 kN/m
LF 2 活荷载:
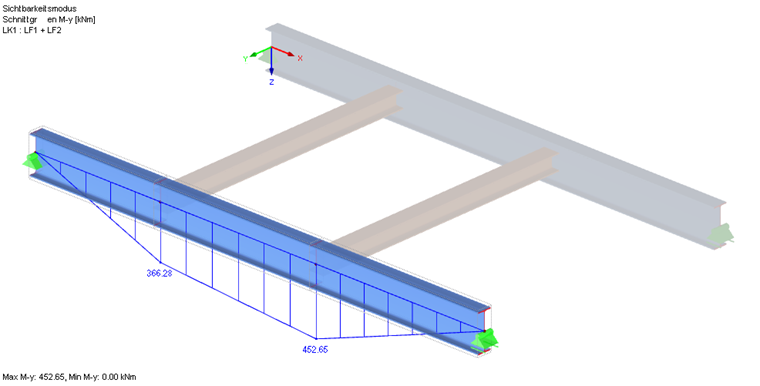
内力设计值
不考虑次梁的稳定性分析按照[3] 6.3.2
假设在杆件'的始端和末端各有一个弯扭屈曲约束,在 RF‑STEEL EC3 中按照[3]的验算确定了理想的弯扭屈曲临界弯矩 Mcr为 368 kNm ] ,第 6.3.2 条。 按照公式 6.54 的验算方法,其比值为 1,64。 因此可以得出,如果不考虑次梁对主梁的侧向支撑稳定作用,主梁的稳定性验算不满足规范要求。
考虑次梁的稳定性分析按照[3] ,附录 BB.2.2
欧洲钢结构规范 EN 1993-1-1 附录 BB.2.2 的规定假设在梁的长度方向上布置连续的转动约束。 首先需要布置独立的转动约束,然后将在下一步的计算中与结构构件“融合”成一个整体的转动约束。
计算当前的连续转动约束:
数值取自[2] ,并仅根据附录 BB.2.2 中的符号进行调整。
Cθ,R,k = 11.823 kNm (由于次梁的弯曲变形而产生的分量)
Cθ,D,k = 359 kNm (由于主梁的截面变形,考虑到腹板上的连接)
按照次梁平均间距计算连续转动约束 Cθ:
计算需要的转动约束:
值:
Kυ = 0.35 对于弹性截面比
Kθ = 10 按照 DIN EN 1993‑1‑1/NA,表 BB.1
可以将转动约束的最小值 Cθ,min 乘以折减系数 (MEd / Mel,Rd)² :
验算:
Cθ,prov = 134 kNm/m < Cθ,min = 200,9 kNm/m
上述的计算表明,按照附录 BB.2.2 的规定验算次梁对主梁的侧向支撑影响作用所产生的扭转约束验算同样不满足规范要求。
考虑次梁的稳定性分析按照[3]中 6.3.4 条
计算当前的独立转动约束:
数值取自[2] ,并仅根据附录 BB.2.2 中的符号进行调整。
Cθ,R,k = 11.823 kNm (由于次梁的弯曲变形而产生的分量)
Cθ,D,k = 359 kNm (由于主梁的截面变形,考虑到腹板上的连接)
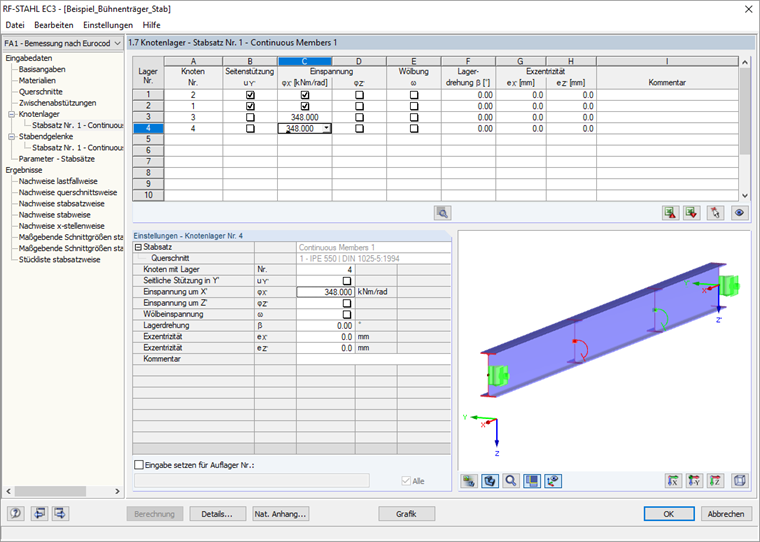
结构模型中多杆件的转动约束可以按照第 6.3.4 节所规定的类型在对话框 1.7 中进行详细设置。
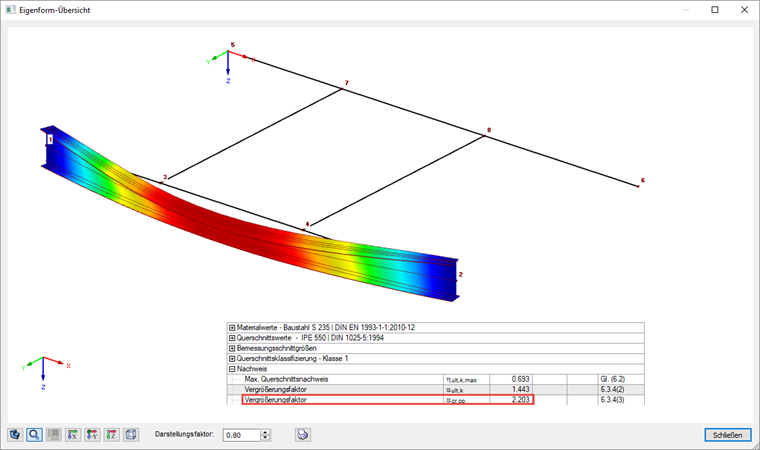
在按照 6.3.4 进行验算期间,在 RF‑STEEL EC3 中应用的特征值分解器确定系数 αcr,op ,在结构系统平面产生变形的情况下可以达到最小的理想临界屈曲荷载。
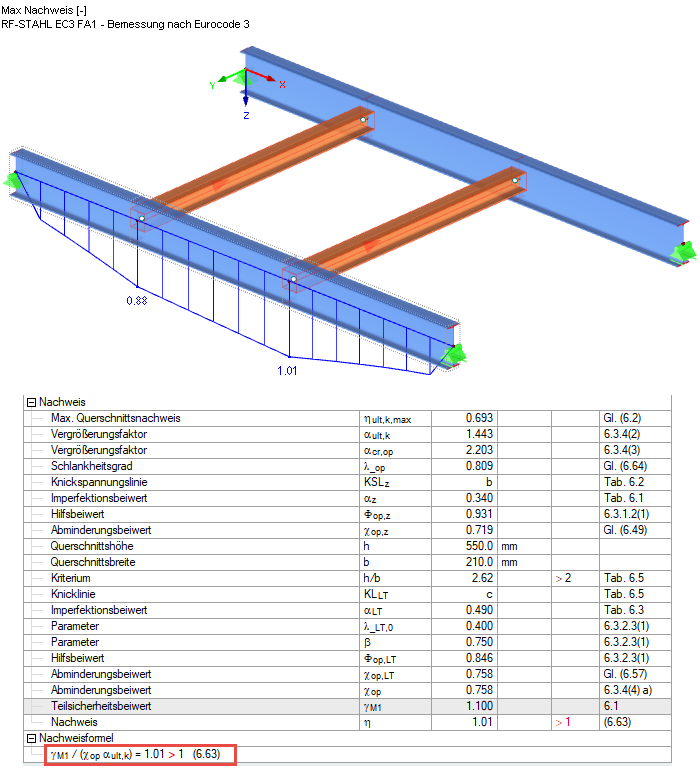
在附加模块中可以详细显示计算中间过程中得出的例如临界屈曲荷载等各个中间结果(见计算结果对话框),另外软件还可以在单独的窗口中显示其相关的特征振型。 结果是Mcr为452.65 kNm∙2.203 = 997.2 kNm。
该结构按照公式 6.63 计算得出的结果为 1.01。 对于 αcr,op的计算,荷载施加点按照详细设置以非稳定的方式施加在上翼缘上。 考虑到荷载作用的实际位置位于上翼缘与剪切中心之间,因此计算结果略微超出规范规定的容许值可以忽略不计,也即是验算结果基本可以满足规范要求。
在有限元分析模型中确定Mcr
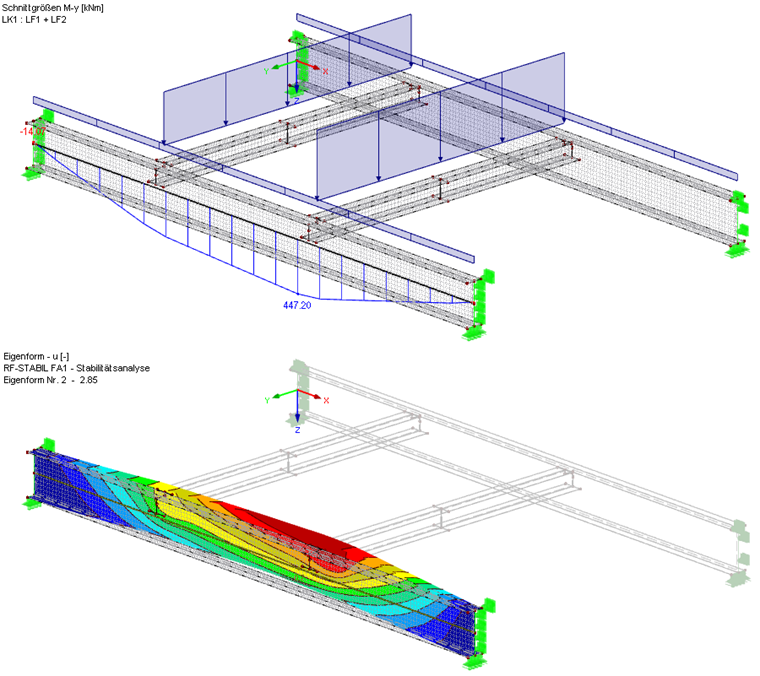
通过使用软件的功能“由杆件生成面”以及其他在 RFEM 中集成的模型生成工具,用户可以非常简洁、迅速的生成有限元的面模型。 使用杆件类型“结果梁”可以确定并以图形方式显示梁中的弯矩 My 。 下一步计算所需要的结构的整体模型的临界屈曲荷载系数可以在附加模块 RF-STABIL 中计算并导出。
使用该有限元模型,我们得到的弯矩 Mcr为 447.20 kNm∙2.85 = 1.274.5 kNm。 该结果比按照设置独立的转动约束的杆件模型所计算的结果略大。 如果需要获得更加精确的计算结果,那么可以考虑创建次梁节点位置细部的有限元模型。