User Story
In questo esempio, andremo a calcolare pressioni locali, pressioni medie e studi parametrici per la progettazione preliminare con metodi più precisi, come l'URANS transitorio.
Questo esempio appartiene al Gruppo 2, secondo la Figura 2.2 del WTG-Merkblatt-M3:
- G2: Valori assoluti con requisiti di accuratezza media. L'area di applicazione può includere parametri o studi preliminari quando sono pianificati studi successivi con maggiore accuratezza (es. esame in galleria del vento di classe G3).
- R2: Solitario, tutte le direzioni del vento rilevanti con risoluzione direzionale sufficientemente fine.
- Z2: Valori medi statistici e deviazioni standard, a condizione che coinvolgano processi di flusso stazionari, per i quali è sufficiente una verifica statistica delle fluttuazioni con un fattore di picco.
- S1: Effetti statici. Sono sufficienti per rappresentare il modello strutturale con il dettaglio meccanico necessario, ma senza proprietà di massa e smorzamento.
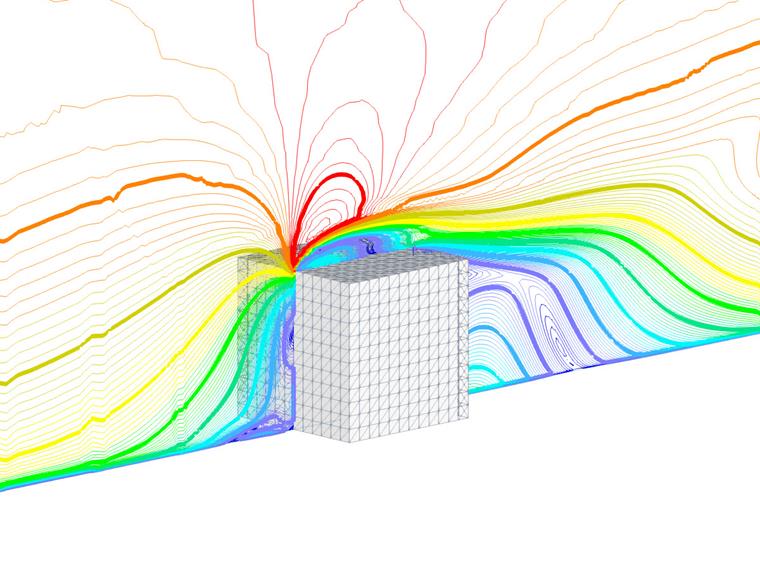
Le dimensioni dell'esempio sono mostrate nella Figura 1 e l'assunzione di input è illustrata nella Tabella 1:
Tabella 1: Dati di Input dell'Esempio del Cubo 3D
| Parametro | Simbolo | Valore | Unità |
|---|---|---|---|
| Velocità del Vento di Base | V | 10.13 | m/s |
| Altezza del Tetto | h | 6 | m |
| Dimensione Orizzontale | α | 6 | m |
| Angolo del Tetto | θroof | 0 | Grado |
| Densità dell'Aria – RWIND | ρ | 1.25 | kg/m³ |
| Direzioni del Vento | θwind | 0 | Grado |
| Modello di Turbolenza – RWIND | RANS & URANS | - | - |
| Viscosità Cinetica (Equazione 7:15, EN 1991-1-4) – RWIND | ν | 1.5×10⁻⁵ | m²/s |
| Ordine dello Schema – RWIND | Primo e Secondo | - | - |
| Valore di Target del Residuo – RWIND | 10⁻⁴ | - | - |
| Tipo di Residuo – RWIND | Pressione | - | - |
| Numero Minimo di Iterazioni – RWIND | 800 | - | - |
| Strato Limite – RWIND | NL | 10 | - |
| Tipo di Funzione di Parete – RWIND | Enhanced / Blended | - | - |
Analisi di Sensibilità
Per l'esempio corrente, l'analisi di sensibilità è mostrata secondo la Figura 2. I risultati delle forze di trascinamento totale sono investigati per quattro diversi numeri di mesh. L'indipendenza dalla mesh è ottenuta a 1.6 milioni di celle (Mesh #4).
Il WTG-Merkblatt M3 fornisce due metodi chiave per la validazione dei risultati delle simulazioni. Il metodo della Hit Rate valuta quanti dei valori simulati Pi corrispondono correttamente ai valori di riferimento Oi entro una tolleranza definita, utilizzando un approccio di classificazione binaria (hit o miss). Questo approccio valuta l'affidabilità della simulazione calcolando un tasso di hit q, simile alle funzioni di confidenza utilizzate nella teoria dell'affidabilità. Al contrario, il metodo del Normalizzato Errore Quadratico Medio (e2) offre una valutazione di accuratezza più dettagliata quantificando la deviazione quadratica media tra valori simulati e di riferimento, normalizzata per tener conto delle differenze di scala. Insieme, questi metodi forniscono misure qualitative e quantitative per la validazione delle simulazioni.
Risultati
Il diagramma nella Figura 3 presenta la distribuzione del Coefficiente di Pressione (Cp) medio e di picco lungo una posizione specificata su una struttura, confrontando risultati sperimentali con simulazioni numeriche utilizzando vari modelli computazionali. I dati sperimentali includono misurazioni dallo studio sul campo Silsoe F-S e test in galleria del vento (WT), mentre le simulazioni sono condotte utilizzando i modelli RWIND RANS e RWIND URANS. Il modello URANS è ulteriormente suddiviso in valori medi e di picco per analizzare in modo completo il comportamento della pressione aerodinamica.
Il confronto nella Figura 4 mira a valutare l'accuratezza dei modelli di simulazione RWIND nel replicare i risultati sperimentali. Metriche statistiche chiave, come il Coefficiente di Correlazione (R) e il Coefficiente di Determinazione (R²), sono presentate per quantificare l'accordo tra dati simulati e sperimentali, offrendo spunti sull'affidabilità di questi modelli per l'analisi aerodinamica. La linea di riferimento diagonale rappresenta una corrispondenza perfetta tra risultati di simulazione ed esperimenti, e la vicinanza dei punti dati a questa linea riflette l'accuratezza di ciascun modello. La differenza tra RWIND e l'Eurocodice è di circa Wrel,RANS = 11.54% e Wrel,URANS = 21.46%; quindi, il tasso di hit può essere ottenuto come qRANS=59% e qURANS,10%=30% e qURANS,20%=63%. L'errore quadratico medio normalizzato è calcolato rispettivamente; e2RANS=0.02 e e2URANS=0.04.
Il modello è disponibile per il download gratuito qui: