Histoire d’utilisateur
Dans cet exemple, nous allons calculer les pressions locales, les pressions moyennes, et les études de paramètres pour le calcul préliminaire avec des méthodes plus précises, telles qu’URANS transitoire.
Cet exemple appartient au Groupe 2, selon la figure 2.2 de WTG-Merkblatt-M3 :
- G2 : valeurs absolues avec exigences de précision moyennes. L’aire d’application peut inclure des paramètres ou des études préliminaires lorsque des enquêtes ultérieures avec une précision plus élevée sont prévues (par exemple, essai en soufflerie de classe G3).
- R2 : isolées, toutes les directions de vent concernées avec une résolution directionnelle suffisamment fine.
- Z2 : valeurs moyennes statistiques et écarts types, à condition qu’ils impliquent des processus de flux stationnaire, pour lesquels une vérification statistique des fluctuations avec un facteur de pointe est suffisante.
- S1 : effets statiques. Ils suffisent pour représenter le modèle structurel avec le niveau de détail mécanique requis, mais sans propriétés de masse et d’amortissement.
Les dimensions de l’exemple sont montrées à la figure 1, et l’hypothèse d’entrée est illustrée dans le Tableau 1 :
Tableau 1 : Données d’entrée de l’exemple de cube 3D
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Vitesse de vent de base | V | 10,13 | m/s |
| Hauteur de la toiture | h | 6 | m |
| Dimension horizontale | α | 6 | m |
| Angle de la toiture | θroof | 0 | Degré |
| Densité de l’air – RWIND | ρ | 1,25 | kg/m³ |
| Directions du vent | θwind | 0 | Degré |
| Modèle de turbulence – RWIND | RANS & URANS | - | - |
| Viscosité cinématique (Équation 7:15, EN 1991-1-4) – RWIND | ν | 1,5×10⁻⁵ | m²/s |
| Ordre du schéma – RWIND | Premier et Second | - | - |
| Valeur cible de résidu – RWIND | 10⁻⁴ | - | - |
| Type de résidu – RWIND | Pression | - | - |
| Nombre minimal d’itérations – RWIND | 800 | - | - |
| Couche limite – RWIND | NL | 10 | - |
| Type de fonction de paroi – RWIND | Augmenté / Combiné | - | - |
Analyse de sensibilité
Pour l’exemple actuel, l’analyse de sensibilité est montrée par la figure 2. Les résultats des forces de traînée totales sont étudiés pour quatre nombres de maillage différents. L’indépendance du maillage est obtenue à 1,6 million de cellules (Maillage #4).
WTG-Merkblatt M3 fournit deux méthodes clés pour valider les résultats de simulation. La méthode du taux de réussite permet d’évaluer combien des valeurs simulées Pi correspondent correctement aux valeurs de référence Oi dans une tolérance définie, en utilisant une approche de classification binaire (réussite ou échec). Cette approche évalue la fiabilité de la simulation en calculant un taux de réussite q, similaire aux fonctions de confiance utilisées dans la théorie de la fiabilité. En revanche, la méthode Erreur quadratique moyenne normalisée (e2) offre une évaluation de précision plus détaillée en quantifiant l’écart quadratique moyen entre les valeurs simulées et de référence, normalisée pour tenir compte des différences d’échelle. Ensemble, ces méthodes fournissent des mesures qualitatives et quantitatives pour la validation des simulations.
Résultats
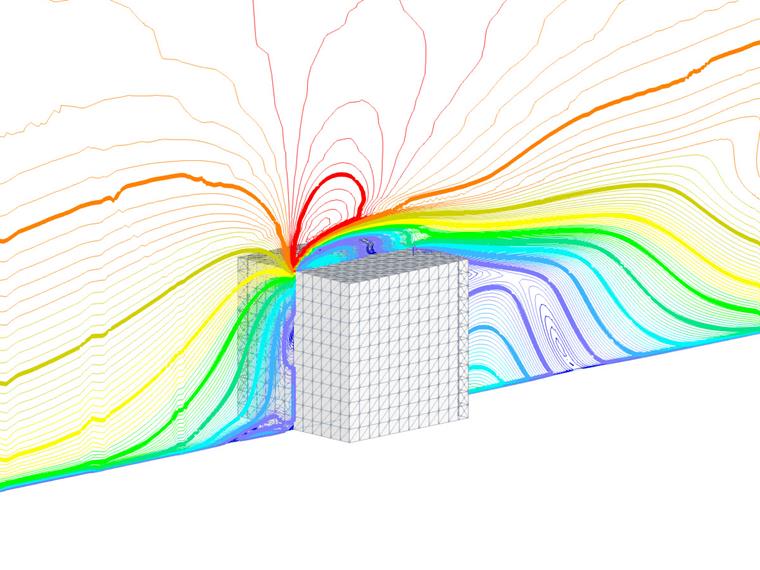
Le diagramme de la figure 3 présente la distribution du coefficient de pression moyen et de pointe (Cp) le long d’une position spécifiée sur une structure, comparant les résultats expérimentaux aux simulations numériques utilisant divers modèles de calcul. Les données expérimentales incluent des mesures de l’étude de terrain Silsoe F-S et des essais en soufflerie (WT), tandis que les simulations sont effectuées en utilisant les modèles RWIND RANS et RWIND URANS. Le modèle URANS est en outre divisé en valeurs moyennes et de pic pour analyser de manière exhaustive le comportement de la pression aérodynamique.
La comparaison dans la figure 4 vise à évaluer la précision des modèles de simulation RWIND pour reproduire les résultats expérimentaux. Des métriques statistiques clés, telles que le coefficient de corrélation (R) et le coefficient de détermination (R²), sont présentées pour quantifier la concordance entre les données simulées et expérimentales, offrant un aperçu de la fiabilité de ces modèles pour l’analyse aérodynamique. La ligne de référence diagonale représente une correspondance parfaite entre les résultats de simulation et expérimentaux, et la proximité des points de données à cette ligne reflète la précision de chaque modèle. La différence entre RWIND et l’Eurocode est d’environ Wrel,RANS = 11,54 % et Wrel,URANS = 21,46 %. Alors les taux de réussites qRANS=59 %, qURANS,10 %=30 % et qURANS,20 %=63 % peuvent être obtenus. L’erreur quadratique moyenne normalisée est calculée respectivement ; e2RANS=0,02 et e2URANS=0,04.
Le modèle est disponible au téléchargement gratuit :