User Story
W tym przykładzie obliczymy lokalne ciśnienia, uśrednione ciśnienia oraz przeprowadzimy studium parametrów dla wstępnego projektowania z użyciem bardziej dokładnych metod, takich jak przejściowy URANS.
Przykład ten należy do Grupy 2, zgodnie z Rysunkiem 2.2 w WTG-Merkblatt-M3:
- G2: Wartości absolutne z umiarkowanymi wymaganiami dotyczącymi dokładności. Obszar zastosowania może obejmować parametry lub badania wstępne, gdy planowane są późniejsze badania o wyższej dokładności (np. badanie w tunelu aerodynamicznym klasy G3).
- R2: Samotne, wszystkie istotne kierunki wiatru z wystarczająco dokładną rozdzielczością kierunkową.
- Z2: Wartości średnie i odchylenia standardowe statystyczne, pod warunkiem, że dotyczą stacjonarnych procesów przepływowych, dla których wystarczająca jest statystyczna weryfikacja fluktuacji z współczynnikiem szczytu.
- S1: Efekty statyczne. Są wystarczające do reprezentacji modelu strukturalnego z niezbędnymi szczegółami mechanicznymi, ale bez cech masowych i tłumienia.
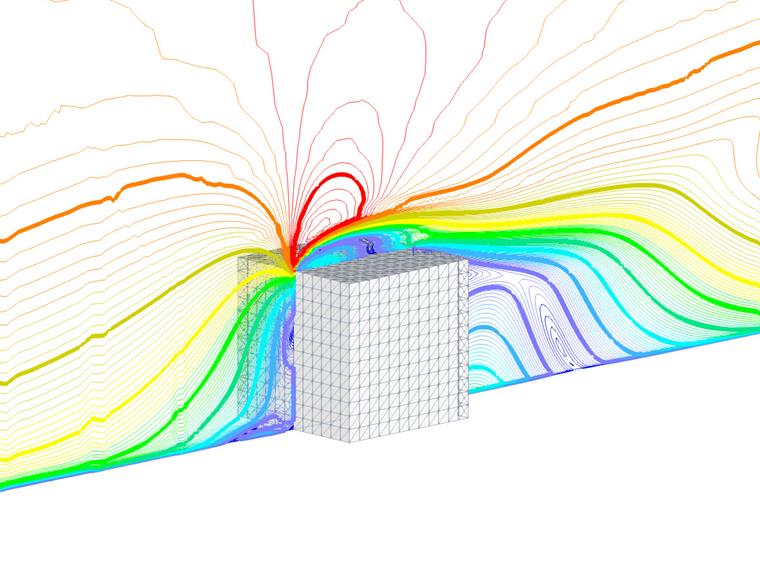
Wymiary przykładu przedstawiono na Rysunku 1, a założenie wejściowe jest zobrazowane w Tabeli 1:
Tabela 1: Dane wejściowe przykładu sześcianu 3D
| Parametr | Symbol | Wartość | Jednostka |
|---|---|---|---|
| Podstawowa prędkość wiatru | V | 10.13 | m/s |
| Wysokość dachu | h | 6 | m |
| Wymiar poziomy | α | 6 | m |
| Kąt dachu | θroof | 0 | Stopień |
| Gęstość powietrza – RWIND | ρ | 1.25 | kg/m³ |
| Kierunki wiatru | θwind | 0 | Stopień |
| Model turbulencji – RWIND | RANS & URANS | - | - |
| Lepkość kinematyczna (Równanie 7:15, EN 1991-1-4) – RWIND | ν | 1.5×10⁻⁵ | m²/s |
| Rząd schematu – RWIND | Pierwszy i Drugi | - | - |
| Docelowa wartość resztkowa – RWIND | 10⁻⁴ | - | - |
| Typ resztki – RWIND | Ciśnienie | - | - |
| Minimalna liczba iteracji – RWIND | 800 | - | - |
| Warstwa graniczna – RWIND | NL | 10 | - |
| Typ funkcji ściennej – RWIND | Ulepszona / Mieszana | - | - |
Analiza wrażliwości
Dla bieżącego przykładu, analiza wrażliwości jest przedstawiona zgodnie z Rysunkiem 2. Wyniki całkowitych sił oporów są badane dla czterech różnych liczb siatek. Niezależność siatki uzyskano przy 1,6 miliona komórek (Siatka #4).
WTG-Merkblatt M3 dostarcza dwie kluczowe metody walidacji wyników symulacji. Metoda Hit Rate ocenia, ile z symulowanych wartości Pi poprawnie odpowiada wartościom referencyjnym Oi w obrębie zdefiniowanej tolerancji, używając binarnego podejścia klasyfikacyjnego (trafienie lub brak trafienia). Podejście to ocenia niezawodność symulacji, obliczając stopę trafień q, podobnie jak funkcje ufności używane w teorii niezawodności. W przeciwieństwie do tego, metoda Znormalizowanego Średniego Błędu Kwadratowego (e2) oferuje bardziej szczegółową ocenę dokładności poprzez określanie średniej kwadratowej odchylenia między wartościami symulowanymi a referencyjnymi, znormalizowanej, aby uwzględnić różnice skali. Razem te metody dostarczają zarówno jakościowych, jak i ilościowych miar walidacji symulacji.
Wyniki
Diagram na Rysunku 3 przedstawia rozkład średniego i szczytowego współczynnika ciśnienia (Cp) wzdłuż określonej pozycji na strukturze, porównując wyniki eksperymentalne z symulacjami numerycznymi przy użyciu różnych modeli obliczeniowych. Dane eksperymentalne zawierają pomiary z badania terenowego Silsoe F-S i testy w tunelu aerodynamicznym (WT), podczas gdy symulacje są przeprowadzane z użyciem modeli RWIND RANS i RWIND URANS. Model URANS jest dodatkowo podzielony na wartości średnie i szczytowe, aby kompleksowo przeanalizować zachowanie ciśnienia aerodynamicznego.
Porównanie na Rysunku 4 ma na celu ocenę dokładności modeli symulacyjnych RWIND w odtwarzaniu wyników eksperymentalnych. Kluczowe metryki statystyczne, takie jak współczynnik korelacji (R) i współczynnik determinacji (R²), są prezentowane w celu określenia zgodności między danymi symulowanymi a eksperymentalnymi, oferując wgląd w niezawodność tych modeli do analizy aerodynamicznej. Linia odniesienia diagonalna reprezentuje doskonałą zgodność między wynikami symulacji a eksperymentalnymi, a bliskość punktów danych do tej linii odzwierciedla dokładność każdego modelu. Różnica między RWIND a Eurokodem wynosi około Wrel,RANS = 11.54% i Wrel,URANS = 21.46%; wtedy stopa trafień może być uzyskana jako qRANS=59% i qURANS,10%=30% oraz qURANS,20%=63%. Znormalizowany średni błąd kwadratowy jest obliczany odpowiednio; e2RANS=0.02 i e2URANS=0.04.
Model jest dostępny do bezpłatnego pobrania tutaj: