Описание работы
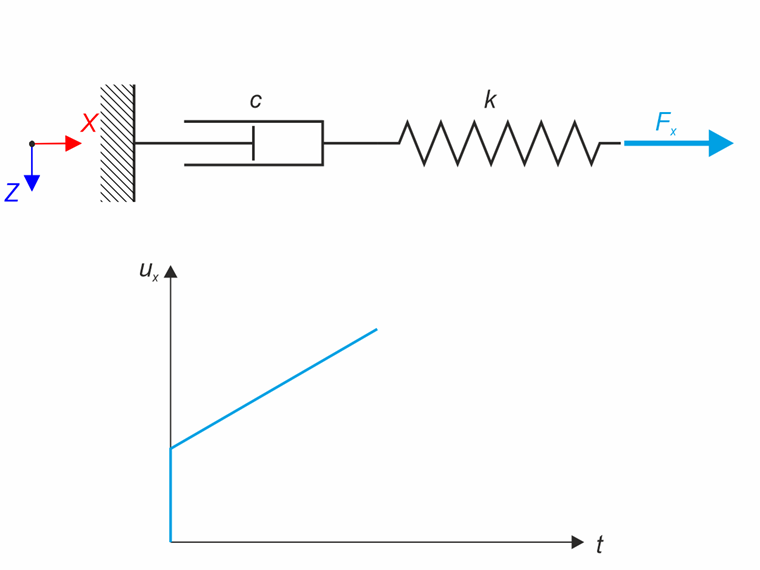
Модель материала Максвелла состоит из последовательно соединенных линейной пружины и вязкого амортизатора. В данном контрольном примере мы протестируем поведение данной модели во времени. Модель материала Максвелла загружена постоянной силой Fx. Эта сила вызывает благодаря пружине начальную деформацию, а затем деформация увеличивается во времени благодаря амортизатору. Деформация наблюдается во время нагрузки (20 с) и в конце расчета (120 с). Применяется для анализа изменений во времени линейный неявный метод Ньюмарка.
| Свойства системы | Пружина | Жесткость | k | 100,000 | кН/м |
| амортизатор | Вискозное затухание | c | 1000,000 | кНс/м | |
| Нагрузки | Сила | Fx | 1,000 | кН | |
Аналитическое решение
Модель материала Максвелла представляет собой последовательное соединение пружины и амортизатора. Напряжение в пружине σe и напряжение в амортизаторе σv одинаково (σe = σv = σ). Общая деформация в данной модели задается следующим образом:
Данную формулу можно изменить для получения деформации модели материала Максвелла в конкретное время, учитывая, что нагружение начинается в момент времени t0.
Затем можно рассчитать деформацию в момент времени 20 с и 120 с, см. результаты.
Настройки программы RFEM и RSTAB
- Смоделировано в программе RFEM 6.05
- Используется Анализ изменений во времени с диаграммой времени
- Используется линейный неявный метод Ньюмарка
Результаты
| Количество | Любое аналитическое решение | Rfem 6 | сечения |
| ux (t=20) [мм] | 10,000 | 10,005 | 1,001 |
| ux (t=120) [мм] | 110,000 | 110,005 | 1,000 |
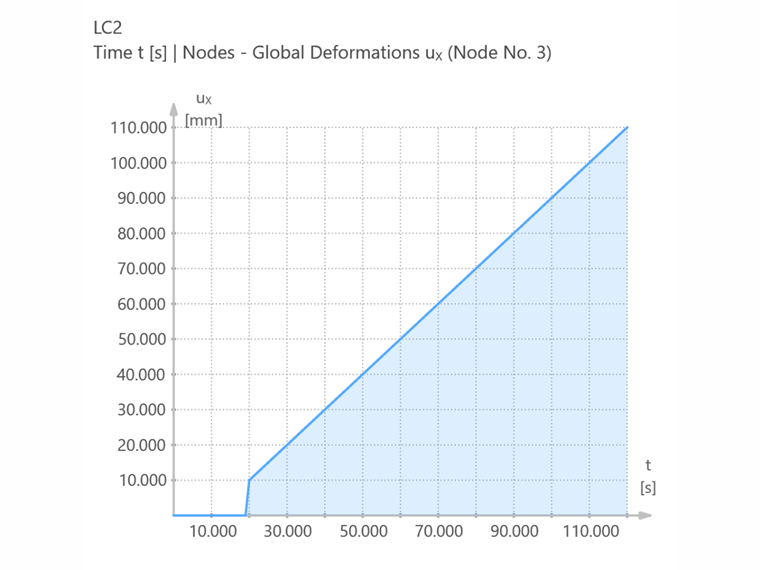
Свойства деформации ux во времени можно увидеть на следующем рисунке.