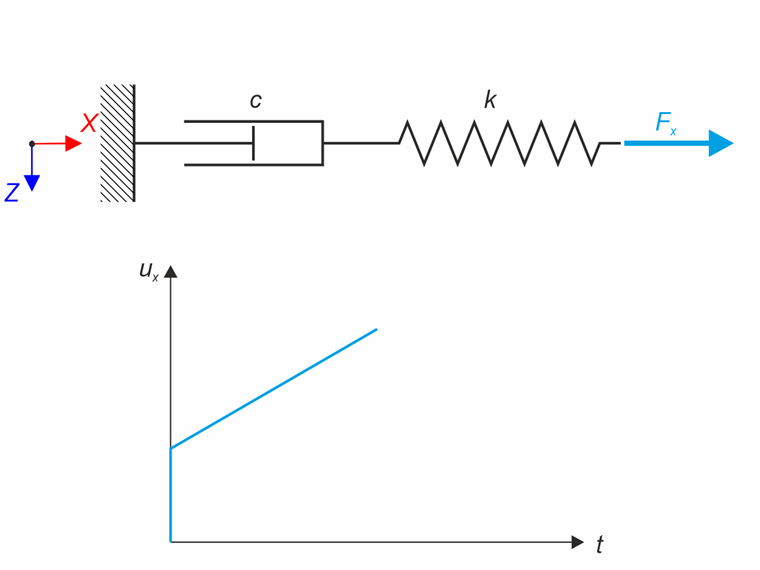
Description
Maxwell material model consists of the linear spring and viscous damper connected in series. In this verification example there is tested the time behaviour of this model. The Maxwell material model is loaded by constant force Fx. This force causes initial deformation thanks to the spring, the deformation is then growing in time due to the damper. The deformation is observed at time of loading (20 s) and at the end of the analysis (120 s). Time History Analysis with Linear Implicit Newmark method is used.
| System Properties | Spring | Stiffness | k | 100.000 | kN/m |
| Damper | Viscous Damping | c | 1000.000 | kNs/m | |
| Load | Force | Fx | 1.000 | kN | |
Analytical Solution
Maxwell material model is a series connection of the spring and damper. The stress in the spring σe and the stress in the damper σv are equal (σe=σv=σ). Total strain of this model is defined as follows:
This formula can be modified to obtain deformation of the Maxwell material model at specific time considering that loading begins at time t0.
Then it is possible to calculate deformation at time 20 s and 120 s, see results.
RFEM and RSTAB Settings
- Modeled in RFEM 6.05
- Time History Analysis with Time Diagram is used
- Linear Implicit Newmark method is used
Results
| Quantity | Anylytical Solution | RFEM 6 | Ratio |
| ux(t=20) [mm] | 10.000 | 10.005 | 1.001 |
| ux(t=120) [mm] | 110.000 | 110.005 | 1.000 |
The time behaviour of the deformation ux can be seen in the following figure.