说明
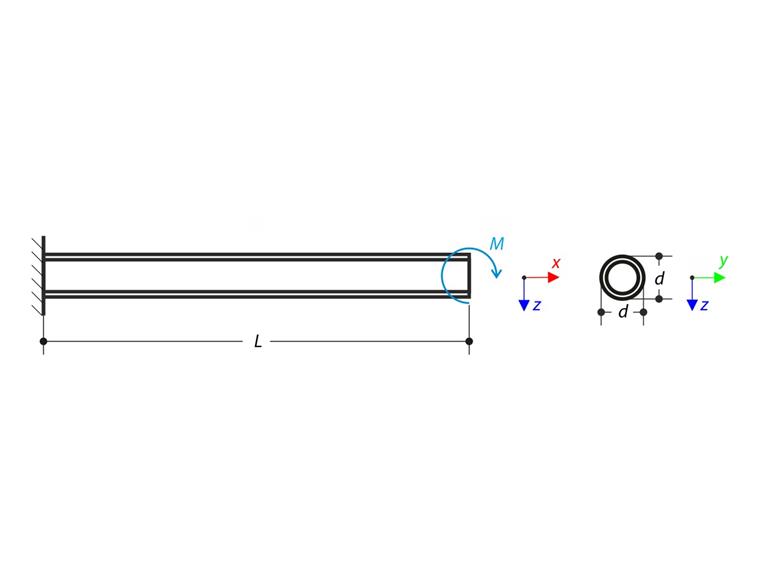
在悬臂自由端施加弯矩 M 通过三阶分析和大变形分析，忽略梁'自重，自由端的最大挠度 ux和 uz 。 验算示例是基于 Gensichen 和 Lumpe 提出的示例（参见参考资料）。
| 材料 | 钢 | 弹性模量 | E | 210000,000 | MPa |
| 剪切模量 | G | 81000,000 | MPa | ||
| 几何尺寸 | 圆管悬臂 | 周长 | l | 4,000 | m |
| 直径 | d | 42,400 | mm | ||
| 墙厚度 | t | 4,000 | mm | ||
| 荷载 | 弯矩 | M | 3,400 | kNm | |
解析解
一阶分析(几何线性)
对于几何线性分析，可以按照欧拉-伯努利方程进行求解。 对于给定的几何形状、荷载和边界条件，最大挠度 uz,max的计算结果如下：
考虑线性分析的挠度 ux,max为零。
大变形分析
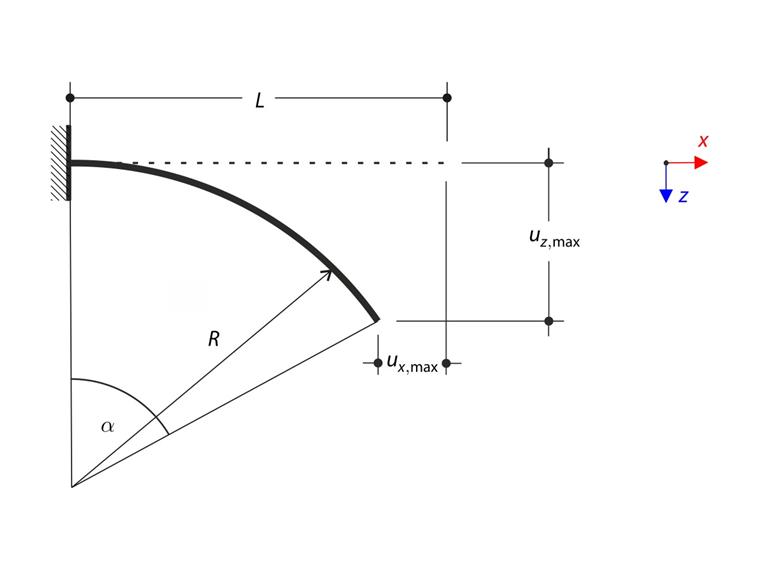
梁在进行大变形分析时，可以通过非线性微分方程描述，如下图所示。
表格右侧的项是常数，左侧的曲率 ε 也是常数。 圆是一个恒定曲率的曲线，因此该问题的解就是半径为 R 的圆弧。
R 是圆弧的半径。 圆弧的角度 α 等于 α=L/R。
RFEM 和 RSTAB 设置
- 在RFEM 5.05、RSTAB 8.05 和 RFEM 6.01、RSTAB 9.01 中建模
- 单元尺寸 lFE = 0.400 m
- 增量数目为 5
- 使用各向同性线弹性材料模型
- 激活杆件抗剪刚度
- 激活大变形或超临界分析的杆件划分
结果输出
| 解析解 | RFEM 6 | 比值 | RSTAB 9 | 比值 | |
| 一阶分析(几何线性) | 0,000 | 0,000 | <现在wiki>- | 0,000 | <现在wiki>- |
| 三阶分析 | -0.337 | -0.336 | 0,997 | -0.336 | 0,997 |
| 解析解 | RFEM 6 | 比值 | RSTAB 9 | 比值 | |
| 一阶分析(几何线性) | 1,441 | 1,441 | 1,000 | 1,441 | 1,000 |
| 三阶分析 | 1,379 | 1,380 | 1,001 | 1,380 | 1,001 |
| 解析解 | RFEM 5 | 比值 | RSTAB 8 | 比值 | |
| 一阶分析(几何线性) | 0,000 | 0,000 | <现在wiki>- | 0,000 | <现在wiki>- |
| 三阶分析 | -0.337 | -0.338 | 1,003 | -0.337 | 1,000 |
| 解析解 | RFEM 5 | 比值 | RSTAB 8 | 比值 | |
| 一阶分析(几何线性) | 1,441 | 1,441 | 1,000 | 1,441 | 1,000 |
| 三阶分析 | 1,379 | 1,380 | 1,001 | 1,380 | 1,001 |
,_LC1__LI.jpg?mw=760&hash=8a72fd14929115d349aeafc6a154c475e761a1ac)
,_LC1__LI.jpg?mw=350&hash=a49d4e90c707e57dab1d5ce0c04d5d665393348d)
,_LC1__LI.jpg?mw=350&hash=a49d4e90c707e57dab1d5ce0c04d5d665393348d)
,_LC1__LI.jpg?mw=350&hash=a49d4e90c707e57dab1d5ce0c04d5d665393348d)
,_LC1__LI.jpg?mw=350&hash=a49d4e90c707e57dab1d5ce0c04d5d665393348d)
